Определить объем информации

Определить общее количество (объем) информации следующего афоризма Конфуция: «Величайшая слава не в том, чтобы никогда не ошибаться, но в том, чтобы уметь подняться каждый раз, когда падаешь».  

Общий объем информации определим по следующей формуле:  

где n - число символов в сообщении; а m- число символов алфавита.  

Предположим, что количество символов русского алфавита m=32 (букву «ё» учитывать не будем), тогда  

Следовательно, формула определения общего объема информации примет следующий вид:  

Определим количество символов в заданном информационном сообщении: n=90 (символов, букв). Тогда  

Пусть есть вектор, характеризующий состояние некоторого сообщества относительно распределения однородной информации среди его членов.  

Здесь: , если k-ый индивид не обладает соответствующей информацией; , если k-ый индивид располагает указанной информацией.  

Пусть известна матрица смежности сообщества , описывающая возможные информационные связи членов сообщества. Причем, если то i-ый индивид может передать рассматриваемую информацию j-му индивиду; , если i-ый индивид сделать этого не может.  

Тогда после одного такта информационных обменов состояние сообщества определяется выражением:  

,  

где - вектор начального состояния сообщества, фиксирующий ситуацию получения какими-либо его членами извне рассматриваемой информации; E-единичная диагональная матрица.  

   После двух тактов обмена информацией состояние сообщества определится следующим образом:  

.  

После n-тактов:  

.  

Где - m-ая степень матрицы ; n-общее количество тактов обмена (не актов, а тактов, потому, что некоторые акты обменов могут осуществляться одновременно).  

Если есть период времени между двумя последовательными тактами, то  

   ,  

   где .  

Пусть, например, мы имеем сообщество, состоящее из трех человек. Информационная матрица данного сообщества выглядит таким образом:  

.  

Тогда, если  

,  

нетрудно получить  

;  

.  

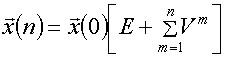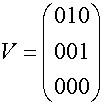Если же , то результат будет иным: , то есть в этом случае первый индивид никогда не узнает той информации, которой располагают второй и третий индивиды.