8. Идеальный и реальный колебательные контура. Основные характеристики колебательного контура (свободные колебания, частота и период свободных колебаний, характеристическое сопротивление, добротность)

Контур состоит из катушки и конденсатора. Идеальный колебательный контур состоит из катушки и конденсатора, но в нём нет сопротивления потерь.

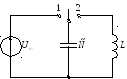
В 1 положении ключа конденсатор заряжается до напряжения источника, в нём накапливается энергия электрического поля .

Во 2 положении конденсатор начинает разряжаться на катушку, и энергия переходит в энергию магнитного поля катушки .

В катушке возникает ЭДС самоиндукции, которая поддерживает ток, и конденсатор снова заряжается, но в другом направлении. Энергия опять переходит в энергию электрического поля конденсатора.

Вывод: конденсатор и катушка обмениваются энергией, т. е. происходит колебание энергии. Такие колебания называются собственными или свободными, т. к. происходят без помощи источника от первоначального запаса энергии.

Эти колебания будут незатухающими. Их амплитуда мс течением времени не будет уменьшаться, т. к. нет сопротивления потерь, и энергия из контура не уходит. Выведем формулу частоты и периода свободных колебаний:

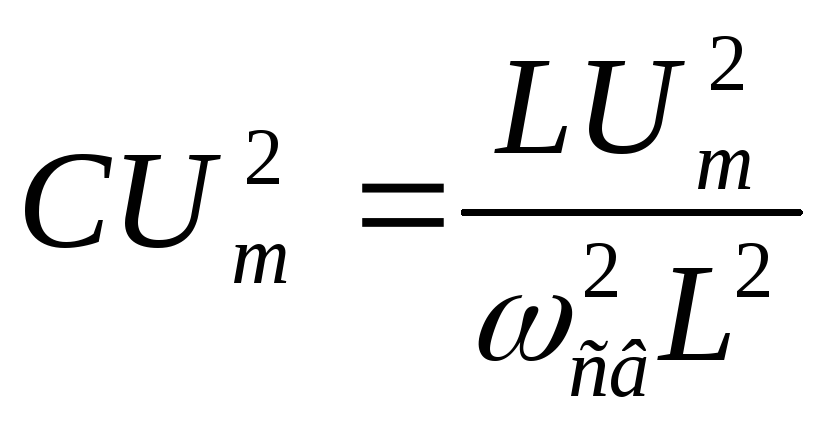
Вывод: частота и период свободных колебаний зависят от L и C, но не зависят от величины приложенного напряжения.

Рассчитаем сопротивление катушки и конденсатора на частоте свободных колебаний.

Вывод: сопротивление катушки и конденсатора на частоте свободных колебаний называется характеристическим:

В реальном контуре существует сопротивление потерь, поэтому колебания будут затухающими, их амплитуда с течением времени будет уменьшаться, т. к. часть энергии будет уходить через сопротивление потерь.

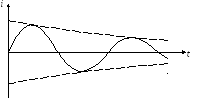
Отношение характеристического сопротивления к резистивному называется добротность:

(безразмерная)

В обычных контурах она составляет единицы – десятки.

Добротность характеризует качество контура. Чем выше добротность, тем медленнее происходят затухания. Величина, обратная добротности, обозначается d — затухание контура:

9. Принципиальная схема последовательного колебательного контура. Резонанс напряжений в последовательном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе напряжений. Резонансная частота, добротность. Настройка колебательного контура в резонанс

Резонанс напряжений

Колебания называются вынужденными, если они происходят под действием источника.

Контур называется последовательным, если катушка и конденсатор соединены последовательно с источником:

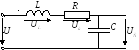
Резонансом называется такое состояние цепи, когда ток и напряжение на входе совпадают по фазе, => .

В последовательном контуре возможен резонанс напряжений.

— условие резонанса напряжений ().

Обычно все параметры цепи, относящиеся к резонансу, записываются с индексом 0, => сопротивление контура в момент резонанса

Сопротивление последовательного контура в момент резонанса минимально.

Свойства цепи при резонансе напряжений

1. 

При резонансе напряжений в контуре течёт максимальный ток.

2. 

При резонансе напряжений напряжения на идеальной катушке и конденсаторе равны.

3. 

На практике и , => и

Вывод: это явление и называется резонанс напряжений, потому что напряжение на идеальной катушке и конденсаторе больше, чем напряжение на входе в момент резонанса.

4. Нарисуем векторную диаграмму:

5. 

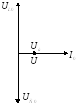
Выводы:

• Т. к. 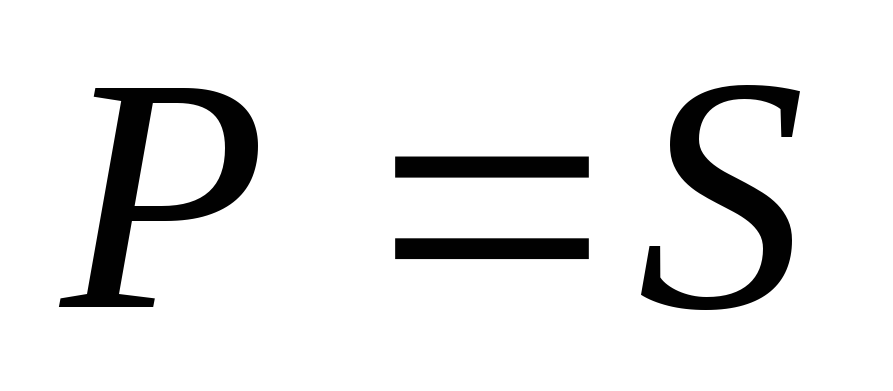, то от источника потребляется только активная мощность.

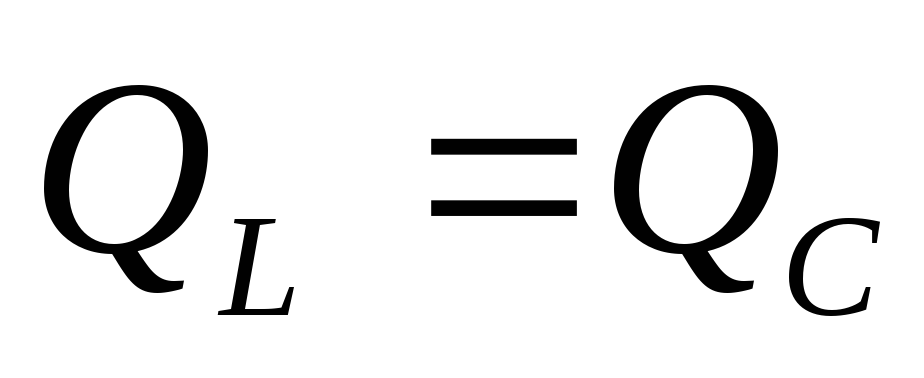• — катушка и конденсатор обмениваются энергией, а т. к. 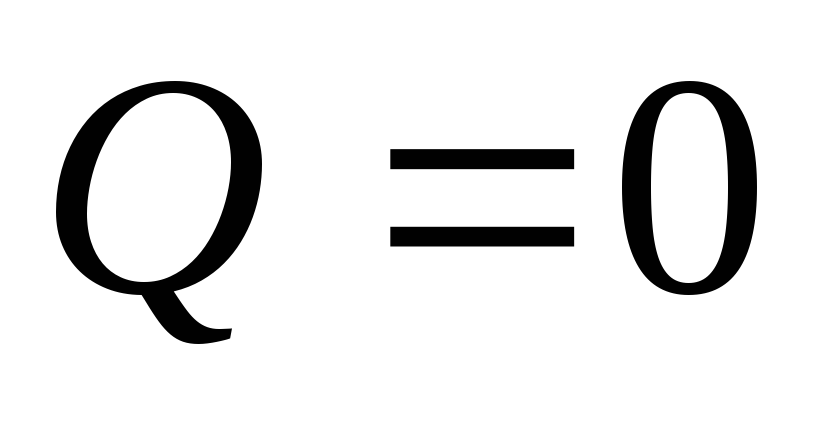, то с источником обмена энергией не происходит.

Резонансная частота, добротность последовательного контура

Выведем формулу резонансной частоты:

Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура .

Настроить контур в резонанс можно:

1. изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;

2. можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.

Т. к. , то можно записать, что .

Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.

Формула добротности:

Вывод: добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.

10. Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной

Расстройка — отклонение частоты от резонансной. Различают:

1. Абсолютная расстройка — разность текущей частоты и резонансной:

Расстройка может и положительной и отрицательной.

2. Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:

3. Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:

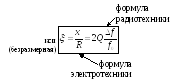
Обычно входные характеристики строят от расстройки.

Входные АЧХ и ФЧХ последовательного контура

, где

— формула входной АЧХ последовательного контура

(на резонансной частоте все расстройки равны 0)

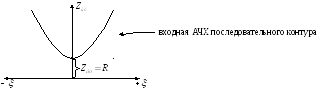
Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение . По мере увеличения расстройки сопротивление контура возрастает.

ФЧХ:

— формула входной ФЧХ последовательного контура

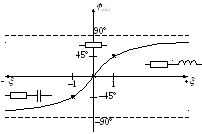
Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: . На частотах меньше резонансной характер сопротивления активно-емкостной, т. к. . На частотах больше резонансной характер сопротивления активно-индуктивный: .