28.Функциональные ряды. Область сходимости ряда, достаточный признак сходимости.

Все члены ряда 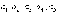 – это ЧИСЛА. Функциональный же ряд состоит из ФУНКЦИЙ: (1) Если вместо x подставить конкретное значение x0,то получится числовой ряд. Если этот ряд сходится, то точка x0— точка сходимости, если расходится—расходимости. Множество всех точек сходимости ф-онального ряда—область сходимости ряда. Достаточный признак сходимости: Если для ряда (1) сущ. знакоположительный сходящийся ряд α1+α2+…+αn+…(2), такой ,что выполняется условие Іu1(x)І<α1,Іu2(x)І<=α2…Іun(x)І<=αn, то ряд(1) также будет сходиться для всех x из области D.

29.Степенные ряды. Радиус сходимости степенного ряда

Степенным рядом называется ф-ональный ряд вида

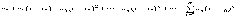₍₁₎   где a₀, a₁, a₂, …,a_n,…, а также x₀ – постоянные числа. Точкуx₀ называют центром степенного ряда. Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида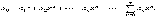 (2)Такой ряд всегда сходится при x=0 и, значит, его область сходимости есть непустое мн-во. Т.( об области сходимости с.р) Если для ряда (2) лимит n ->∞ [an+1/an]=1/R , то областью сходимости ряда (2) является интервал (-R;R) , которому в зависимости от конкретных случаев могут добавляться точки –R,R в интервале сходимости ряд сходится абсолютно , а число R– радиус сходимости с.р. На практике радиус сходимости степенного ряда чаще всего определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда отличны от нуля и сущ. предел _. Тогда радиус сходимости находится по формуле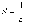 

Действительно, в силу признака Даламбера ряд

 сходится, если число

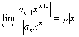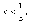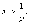 меньше 1, и расходится, если этот предел больше 1. Иначе говоря, ряд сходится для всех x таких, что  и расходится при  Это и означает, что число  является радиусом сходимости ряда

30.Основные теоремы о степенных рядах(с.р) Т1.Сумма степенного ряда есть ф-я непрерывная в области сходимости степенного ряда. Т2.( о дифференцируемости с.р) С.р 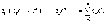 _S(x)(1) в интервале сходимости ( -R;R) почленно продифференцировать , причем полученный ряд сходится в интервале и его сумма Сигма (x)=S'(x). Т3.( об интегрируемости с.р) если с.р(1) имеет интервал сходимости ( -R;R), то ряд a0x+a1x^2/2+…+anx^n+1/n+1+…=γ(x)(2) полученный почленным интегрированием ряда (1) также сходится в этом интеграле причем γ(x)=дифференциал от 0 до x S(t)dt. В общем случае, когда с.р имеет вид a0+a1(x-x0)+a2(x)…поступают след.образом: обозначают (x-x0)=t, получают ряд a0+a1t+a2t+…+ant^n+…, находят радиус сходимости и записывают:-R<t<R -R<x-x0<R x0-R<x<x0+R}интервал сходимости

31. Ряд Тейлора.

Ряд Те́йлора—разлож ф-ции в бесконеч сумму степенных ф-ций. РядыТейлора примен при апроксимации ф-ции многочленами. В частности, линеаризация ур-ий происходит путём разлож в ряд Тейлора и отсеч всех членов выше перв порядка. Пусть ф-ция бесконечн диф-ема в некот окрестности точки . Формальн ряд

наз рядом Тейлора ф-ции в точке .

32. Разложение основных эл-ных ф-й в ряд Тейлора.

1) f(x)=e^x

x₀=0

f’(x)=f”(x)= e^x

х х² хⁿ

e^x=1+1! +2!+…+n!

2)

)

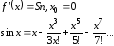
3)

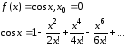
4)

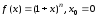
5)