2.2.4 Рекомендации по реализации метода диаграмм (графического метода)

Кинематическое исследование этим методом начинают с построение положений механизмов и траекторий движения точек звеньев

Для исследования кинематики механизмов графически методами необходимо строить несколько положений механизма или определять траекторию движения какой-либо точки ведомого звена. Существует несколько методов построения планов механизма и траекторий движения его звеньев.

Наиболее универсальным является метод засечек (или геометрических мест) его применение дает хорошие результаты при исследовании жесткозвенных механизмов, когда размеры всех звеньев и их перемещения имею один порядок.

Задача об определении планов положений кулачковых механизмов может быть решена двумя методами: методом засечек и методом обращенного движения.

Метод обращенного движения является приближенным методом и может быть рекомендован в случае, если радиусы кривизны профиля кулачка неизвестным.

Для построения планов положения и траектории движения звеньев кулисных механизмов кроме метода засечек можно пользоваться методом модели звена и ложных положений.

Метод модели звена более прост, но менее точен.

В машинах иногда встречаются механизмы, в которых размеры звеньев имеют различный порядок, например, длина кривошип, выполненный в виде эксцентрика порядка 1 мм, а шатун 200 мм. В таких механизмах перемещения отдельных точек звеньев весьма незначительны, что не позволяет использовать для определения траектории движения механизма метод засечек. В этом случае целесообразно пользоваться методами круговых линеек и круговых шаблонов. Методы круговых линеек и шаблонов близки по своей сути, принципиально аналогичны методу засечек, но технически удобны тем, что используется большей масштаб.

Примеры использования различных методов для определения положений механизм и траектории движения точек его звеньев даны в литературе (1), (4), (10).

.

2.3. Рекомендации по выполнению силового анализа быстроходных малонагруженных силами полезного сопротивления машин

Силовой анализ имеет своей задачей изучение влияния внешних сил, сил веса звеньев, сил инерции, сил полезного вредного сопротивления на звенья механизма, на элементы звеньев, на кинематические пары и неподвижные опоры, а также установление способов уменьшения динамических нагрузок, возникающих при движении механизма. Значения этих сил нужны для выполнения расчета на прочность, жесткость, износ деталей (звеньев) механизмов, нагрев кинематических пар, уравновешивания механизмов и для других динамических расчетов, необходимость в которых возникает при проектировании. В частности, например, при выполнении курсовых и дипломных проектов.

В процессе работы быстроходных машин к звеньям ее механизмов обычно приложены внешние силы, а именно: силы движущие, сообщаемые ведущему звену в виде движущего момента и определяемые после силового расчета, задаваемые силы производственных сопротивлений, силы тяжести и др. Кроме того, при движении механизмов в результате реакций связей в кинематических парах возникают силы трения, которые можно рассматривать как составляющие этих реакций. Реакции в кинематических парах, также как и силы трения, по отношению ко всему механизму являются силами внутренними, но по отношению к каждому звену, оказываются силами внешними. Они являются результатом не только действия внешних сил (полезных сопротивлений при обработке), но и действия сил инерции, которые возникают при движении масс звеньев механизма с ускорениями. В большинстве механизмов быстроходных машин эти дополнительные динамические давления в кинематических парах создаваемые силами инерции, превышают по величине собственный вес звеньев и силы полезного сопротивления в сотни раз, поэтому при силовых расчетах таких машин эти нагрузки берутся за основные.

Силы вредного сопротивления, расходуемые на преодоление трения в кинематических парах при проектировании из-за сложности их расчета не учитывают, а при нахождении движущего момента вводят поправочной коэффициент =1.3-1.5

Силовой расчет механизмов может быть произведен различными методами. В настоящее время широко применяется кинетостатический метод. Сущность этого метода сводится к применению для решения задач динамики уравнений равновесия Даламбера. Уравнения составляются исходя из следующих соображений: если к движущей системе, находящейся под действием заданных сил, приложить силы инерции, то в каждый данный момент времени движущуюся систему можно рассматривать как уравновешенную реакциями связей, то есть:

++_u=0,

где - заданные силы или их равнодействующая; - реакции связей или их равнодействующая; _u - силы инерции или их равнодействующая.

Сама движущаяся система рассматривается мгновенно неподвижной и находящейся в равновесии.

Таких образом, составляя для системы обычные уравнения статики и решая их, находят динамические силы, действующие на звенья механизма (обычно реакции в кинематических парах и уравновешивающие силы). Для решений уравнений статики относительно нужно найти величину и направление сил инерции, которые определяются довольно сложно. Сложность их расчета обуславливается тем, что в общем случае каждый момент времени звено быстроходного механизма испытывает действие распределенных сил инерции, изменяющихся по величине, и по направлению в каждой точке звена. Строгий расчет необходимо выполнять с учетом такого характера действующей инерционной нагрузки. Практически, для силового расчета применение схем нагружения звена можно свести к одной равнодействующей, приложенной в центре качания масс, или равнодействующей, приложенной в центре качания масс, или к равнодействующей, приложенной в центре качания масс и моменту. В некоторых случаях удобно применять другой способ упрощения расчета инерциальных нагрузок, так называемый метод замещающих точек.

2.3.1. Определение сил инерции звеньев с использованием метода сведения их к результирующей силе, приложенной в центре масс, и моменту инерции и метода сведения их к результирующей силе, приложенной в центре качения звена.

Звенья механизмов машин в процессе работы совершают различные движения: поступательные, плоскопараллельные, возвратнокачательные и вращательные.

а) Определение инерциальной нагрузки плоскопараллельно движущегося звена (общий случай)

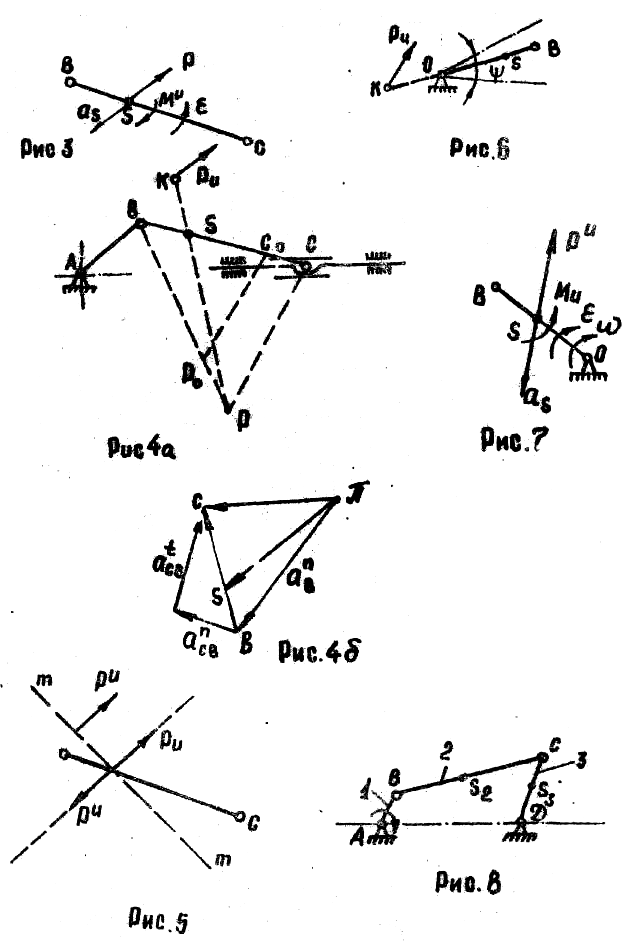
Примером данного движения может служить движение шатуна кривошипно-шатунного механизма - рисунок 3.

Силы инерции шатуна ВС, изображенного на рисунке 3при плоскопараллельном движении могут быть сведены к силе инерции P_и, приложенной в центр масс звена (точка S) и паре сил – моменту инерции M_и , (рисунок 4).

Указанные инерциальные нагрузки определяются как:

_u=-m_s, M_и=-I_s,

где _u - вектор силу инерции звена; m - масса ввела; _s - вектор полного ускорения центра масс звена; I_s - момент инерции звена относительно оси, проходя­щей через центр масс; - угловое ускорение звена.

Если сила инерции _u всегда направлена в сторону обратную -_s, то момент инерции M_и всегда стремится повернуть звено в направлении обратной угловое ускорению звена.

При кинетостатическом расчете силы инерции звена совершающие плоскопараллельное движение, удобно поводить к одной результатирующей силе _u; приложенной в центре качания К звена. Выполняется по следующей последовательности (рис. 4а).

Вначале определяют точку звена ВС, ускорение которой равно нулю (центр ускорения звена). С этой целью, применяя известное в кинематики свойство подобия, на базе линии ВС строят треугольник, подобный и сходственно расположенный треугольнику П_вс плана ускорений (рис. 4,б), для чего откладывают отрезок ВС_о, равный бс, затем, делая высечки циркулем, отрезками ВР_о=в и С_оР_о=с получают треугольник ВР_о=в, равный и сходственно расположенный треугольнику вс.

Далее производят параллельный перенос линии С_оР_о до совпадения точки С_о с точкой С. Пересечение этой линии с продолжением линии ВР_о даст точку Р которая и является центром ускорения. Полученные треугольники ВСР и вс подобны и сходственно расположены. Теперь соединим точку Р и S, и на продолжении этой линии на расстоянии SK от точки S находится центр качания К. При этом величина отрезка SK будет равна:

SK=J_s/mpS.

Следует помнить, что центр ускорения Р, центр масс S и центр качания K всегда располагаются в указанной последовательности.

К найденному указанным образом, центру качания К звена ВС, прикладывают результирующую силу инерции P_u звена, направив ее в сторону противоположную направлению полного ускорения центра S масс звена, т. е., обратно вектору S построения необходимо выполнять для каждого исследуемого положения механизма (звена).

Замена вид инерции звена одной результирующей силой, приложенной в центре качания, может быть выполнена другим способом, исходя из следующих соображений (рис. 5). Рассматривая сложное плоскопараллельное движение звена ВС как состоящее из двух простых движений - поступательного вместе с центром масс и вращательно­го около этого центра, по-прежнему будем иметь силу инерции:

P_u=- ma_{s ,}

и момент силы инерции

M_u=- I_{s ,}

Представим момент M_u как произведение M_u=P_ul. Тогда плечо l пары сил с моментом M_u, соответственно будет равно:

L= M_u/P_u.

Проведем через центр масс S линию n-n, параллельную вектору S. Далее на расстоянии l от линии n-n проведем вектор силы _u в направлении, обратном вектору S, сохраняя при этом знак момента. В нашем случае плечо l откладываем от точки S вверх. Учитывая, что силы P_u, приложенные в центре масс взаимно уничтожились, силы инерции звена опять приведены к одной результатирующей силе P_u, приложенной в ценре качания.

Практически построения в этом случае сводятся к следующему:

Приводим линию m-m через центр масс S звена перпендикулярно вектору ускорения центра масс. На этой линии в ту или иную сторону откладывается плечо l и, сохранив знак момента M_u проводим вектор силы P_u в сторону обратную вектору P_s (ускорению центра масс).

Для определения силы инерции необходимо знать массу звена и его ускорение. Ускорение звена находится при кинематическом исследовании механизма.

Масса звеньев при проектировании быстроходных механизмов выбирается самостоятельно (обуславливается заданием) из опыта проектирования и эксплуатации подобных механизмов, как в отечественной, так и в зарубежной практике. Зная длины звеньев, (выполнен синтез механизма) задаются сечением звеньев и, таким образом, рассчитывают их вес путем умножения удельного веса интервалов, из которого изготовлено звено, на объем последнего. Порядок определения массы звеньев одинаков при любом характере движения звена (поступательном, вращательном, плоскопараллельном и др.)

Для определения момента инерции M_u необходимо располагать знанием углового ускорения звена которое берется также на кинематического анализа механизма:

=a_вс/l_вс,

где a - тангенциальная составляющая ускорения выбранной точки звена; l_вс - длина звена; и момента инерции I_s звена относительно оси, проходящей через центр масс этого звена (массовый момент инерции).

Массовой момент инерции определяют расчетным или эксперимен­тальным путем. При расчетном определении моментов инерции звеньев сложной конфигурации, такие звенья разбиваются на простейшие тела (цилиндр, усеченный конус, куб и др.) и для каждого простейшего тела с массой m_i определяют его момент инерции с I_i относительно оси проходящей черев его центр масс, который является суммой произведений масса каждой частица тела на квадрат ее расстояния от этой оси:

I_i=_ir²_i.

Когда рассчитывают момент инерции звеньев состоящих из нескольких простейших тел, то после определений момента инерции простейших тел относительно оси, проходящей через собственный центр масс, рассчитываются моменты инерции I_Si простейших тел относительно оси, проходящей через общий центр S масс звена:

I_Si=I_i+m_il²_i ,

где I_i расстояние от оси, проходящей через центр масс простейшего тела, до оси проходящей через общий центр масс S звена,

Момент инерции всего звена равен сумме моментов инерции простейших тел:

I_s=I_Si .

Примеры расчета моментов инерции даны в литературе (14), (8). Экспериментальное определение моментов инерции дано в литературе(1), (13).

Описание методов определения сил и моментов инерции дано в литературе (4), (18).

б). Определение инерциальной нагрузки поступательно

движущегося звена.

При движении ползуна кривошипно -ползунного механизма он движется с некоторым ускорением a const, его сила инерции P_U в каждый момент времени равна:

P_u= ma,

где m - масса звена, a - ускорение точек звена.

Сила инерции направлена в сторону, обратную ускорению. Как известно, при данном движении звена =0, а следовательно и M_u=0.

в). Определение инерциальной нагрузки звена, движущегося возвратнокачательно.

Примером может служить движение звена ОВ (рис. 6).

В данном случае, при указанном движении звеньев имеется 0 и а_sО. Инерциальные нагрузки определяются также как показано в разделе 4.6.1. т.е.

P_u=-ma_s; M_u=-Ia_s .

Если сводить все элементарные силы инерции, действующие на звено к одной результатирующей силе, приложенной в центре качания звена, то точка O будет центром ускорения. Центр качания лежит на продолжения линии ОS и расстояние SK будет определятся также

SK= I_s/mPS .

Результирующая сила инерции также будет приложена в центре качания и по величине равна:

P_u=-ma_s .

Направление ее будет обратным направлению полного ускорения центра масс S звена OB.

г). Определение инерциальной нагрузки вращательно движущегося звена.

Примером может служить любое ведущее (приводное) звено (рис.7). В шейных машинах приводные зренья могут двигаться с угловой ско­ростью постоянной величины, т.е. w=const и переменной wconst.

Если при вращении главного вала (кривошипа) швейной машины, считать, что w=const, т. е. a=0 и =0, а центр масс совпадает о центром вращения самого вала, то результирующие сил инерции и моментов равны нулю т.е. P_u=0 и M_u=0.

В общем случае угловая скорость w =const, а центр масс не совпадает с осью вращения 0 звена ВО.

Тогда сила инерции, приложенная в точке S масс звена, равна: Р_u=-ma_s, а момент сил инерции M_u, равен: M_u=I_s.

В общем случае сила инерции и момент также могут быть заменена одной результирующей силой P_u приложенной в центре качания звена методика определения которого описана выше.

Литература: (1), (14), (18).