4. Загальна теорія кривих другого порядку.
24. Звести до канонічного вигляду рівняння кривої:
Розв'язання.
1.
В даному рівнянні
.
2.
Складемо характеристичне рівняння
кривої:
.
Знайдемо
його корені:
.
3. Обчислимо тангенс кута повороту координатних осей:
.
(
,
тобто ці два кута визначають взаємно
перпендикулярні напрями).
З
рівності
випливає,
що кут повороту може знаходитись в
першій
або в третій четвертях, а з
ясно,
що кут повороту
може
знаходитись в другій або четвертій
чвертях.
Зручно
завжди брати для
з
двох можливих значень - додатне, а кут
повороту
-
в першій чверті
. Таким чином, з двох
можливих значень тангенса беремо
.
4.
За
формулами
знайдемо
і
:
і
Потім,
за формулами
,
,
,
,
знайдемо коефіцієнти при змінних в
новому рівнянні:
,
,
,
Рівняння
кривої в системі
буде
мати вигляд:
.
1. За допомогою паралельного переносу системи координат одержане рівняння приведемо до канонічного вигляду. Для цього групуємо члени, які містять одну і ту ж змінну, і одержимо
.
Коефіцієнти при старших членах треба винести за дужки:
В кожній дужці виділимо повний квадрат:
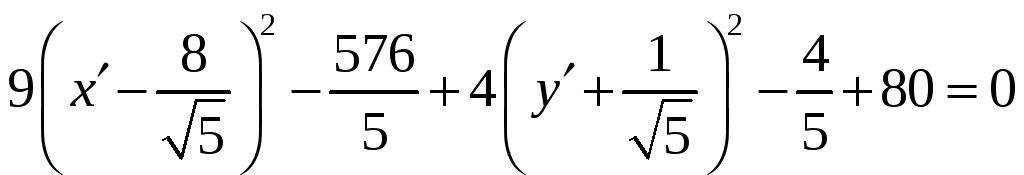
Або
(1)
Виконаємо
тепер паралельний перенос координатної
системи
.
Формули
перетворення запишемо так:
, звідки
(2)
Введемо
позначення в рівняння (1):
Порівнюючи
ці позначення з формулами (2), отримаємо,
що
,
,
а
рівняння (1) запишемо так:
або
Отже,
задане рівняння визначає еліпс. Вигляд
заданої кривої показано
на рис. 1.2.4.1. Можна довести, що точка О'
-
центр еліпса в заданій
системі координат (ХОУ)
має
координати
.
25.
Спростити рівняння кривої
і схематично побудувати
цю криву.
Розв'язання.
Групуємо
члени з однойменними координатами:
,
або
.
Доповнюємо в дужках до повного квадрату
або
.
(а)
Позначаємо:
.
Знаходимо
координати нового початку:
,
,
тобто новий
початок координат знаходиться в точці
.
Рівняння
(а) в новій системі координат приймає
вигляд:
,
або
.
Задане
рівняння визначає параболу з вершиною
в точці
,
віссю
симетрії
паралельною
осі ординат і параметром
(рис. 1.2.4.2).
26. Привести до найпростішого вигляду рівняння кривої
Розв'язання.
Дане рівняння не містить члена з добутком координат. Збираємо в цьому рівнянні члени, що містять однойменні координати
Доповнюємо вираз в дужках до повних квадратів:
,або
Це рівняння не може мати місця при дійсних значеннях х і у. Тому рівняння не визначає ніякої лінії на площині.
27. Привести до найпростішого вигляду рівняння кривої
Розв'язання.
Дане рівняння може бути записане так:
,
або
.
Ця
рівність має місце тільки при
і
.
Тому
дане рівняння визначає на площині одну
точку
.
28.
Знайти два спряжених діаметри кривої
,з
яких один проходить через початок
координат.
Розв'язання.
Дана
крива центральна, тому що
.
Рівняння
її діаметра буде
,
де
- кутовий
коефіцієнт спряженого діаметра.
Так
як шуканий діамегр проходить через
початок координат, то вільний
член його рівняння повинен дорівнювати
нулю, тобто
,
звідки
.
Підставивши значення параметра в
загальне
рівняння діаметра і перетворивши його,
одержимо:
.
Це
рівняння одного із шуканих діаметрів,
його кутовий коефіцієнт
,
отже, рівняння спряженого йому діаметра
буде:
,
або
.
Відповідь:
,
або
.
32.
Знайти вісь параболи
.
Розв'язання.
Усі
діаметри даної параболи мають кутовий
коефіцієнт
.
Вісь
параболи є діаметр, спряжений
перпендикулярним хордам, тобто
хордам з кутовим коефіцієнтом
.
Рівняння
всякого діаметра цієї параболи буде
мати вигляд
,
при
ми
одержимо рівняння осі:
.
Відповідь:
