
- •Криві другого порядку. Їх канонічні рівняння і властивості. Загальна теорія кривих другого порядку.
- •Еліпс. Канонічне рівняння, властивості.
- •Гіпербола.
- •Рівняння еліпса, гіперболи і параболи в полярних координатах.
- •Загальна теорія кривих другого порядку.
- •Центр лінії другого порядку.
- •Асимптотичні напрямки кривих другого порядку.
- •Діаметри лінії другого порядку. Спряжені напрямки. Осі.
- •1. Коло.
- •2. Еліпс. Його властивості.
- •3. Гіпербола, парабола, геометричні властивості кривих другого порядку.
- •4. Загальна теорія кривих другого порядку.
- •Задачи, з яких складається індивідуальне завдання.
- •1. Коло.
- •2. Еліпс. Його властивості.
- •3. Гіпербола, порабола геометричні властивості кривих іншого порядку.
- •4. Спрощення рівняння кривої другого порядку за допомогою перетворення системи координат.
- •5. Асимптоти. Дотичні до кривих другого порядку.
- •Література.
Криві другого порядку. Їх канонічні рівняння і властивості. Загальна теорія кривих другого порядку.
Короткі теоретичні відомості
КРИВІ ДРУГОГО ПОРЯДКУ. ЇХ КАНОНІЧНІ РІВНЯННЯ І ВЛАСТИВОСТІ. Коло.
Означення 1. Коло - це геометричне місце точок площини, рівновіддалених від однієї і тієї ж точки цієї площини (центра)(рис. 1.1.1).
Рівняння
кола з центром в точці
![]() і
радіусом r
має
вигляд:
і
радіусом r
має
вигляд:
![]() (1)
(1)
В окремому випадку, коли центр кола співпадає з початком координат, його рівняння має вигляд:
![]() (2)
(2)
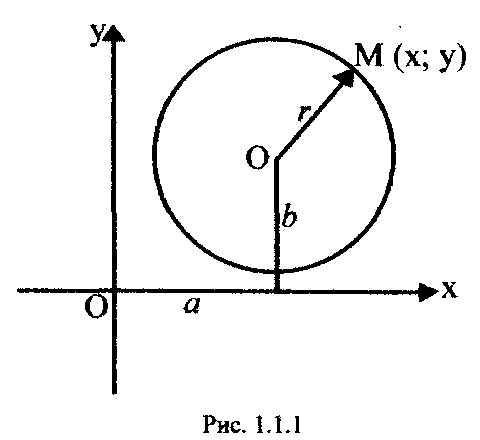
Загальне рівняння кривої другого порядку
![]()
являє собою коло, якщо коефіцієнти при квадратах координат рівні між собою, тобто А=С , і якщо відсутній член з добутком координат ху, тобто B = 0.
Для знаходження точки перетину кола (1) і прямої Ах + Ву + С = 0, треба спільно розв'язати ці два рівняння. Виключивши з них одну з координат, наприклад у, одержимо квадратне рівняння відносно абсциси точки перетину:
1) якщо квадратне рівняння має дійсні і різні корені (підкореневий вираз додатній), то коло і пряма мають дві різні точки перетину, пряма є січною;
2) якщо квадратне рівняння має дійсні, але рівні корені (підкореневий вираз дорівнює нулю), то обидві точки перетину зливаються в одну пряму і пряма дотикається до кола;
3) якщо квадратне рівняння має уявні корені (підкореневий вираз від'ємний), то коло і пряма не мають дійсних точок перетину, пряма проходить за межами кола.
Взаємне
розташування точки
![]() і кола (2)
визначається такими умовами:
і кола (2)
визначається такими умовами:
-
якщо
 то точка
то точка
 лежить
на колі;
лежить
на колі; -
якщо
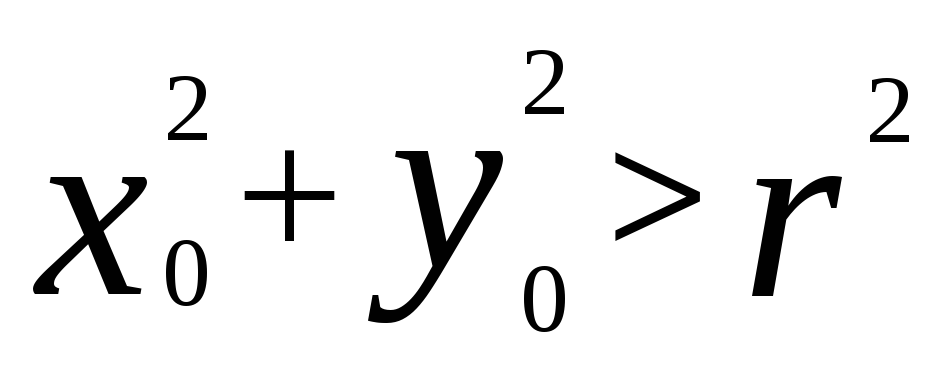 ,
то
точка
,
то
точка
 лежить
за межами кола;
лежить
за межами кола; -
якщо
 ,
то точка
,
то точка
 лежить
всередині кола.
лежить
всередині кола.
Якщо
![]() -
довільна точка кола, то дотична до кола
в цій точці
має рівняння:
-
довільна точка кола, то дотична до кола
в цій точці
має рівняння:
![]() ,
або
,
або
![]() ,
,
в залежності від того, визначається чи ні коло рівнянням (1), або (2).
Еліпс. Канонічне рівняння, властивості.
Означення 2. Еліпсом називається геометричне місце точок площини, для кожної з яких сума відстаней до двох даних точок тієї ж площини, які називаються фокусами, є величина постійна, рівна 2а. (рис. 1.1.2)
Канонічне рівняння еліпса має вигляд:
![]()
де
а
-
велика, b
-
мала піввісь еліпса, причому а,
b,
с (с –
половина відстані
між фокусами) зв'язані співвідношенням,
![]() ,
а>с.
,
а>с.
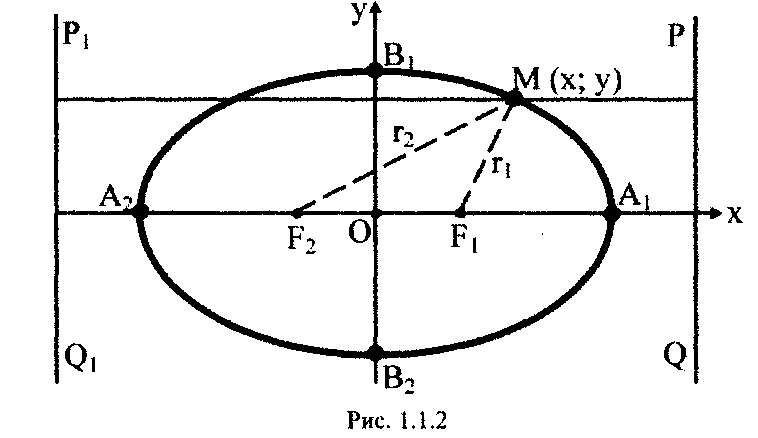
Координати
фокусів еліпса:
![]() і
і
![]() .
.
Відстань між фокусами еліпса дорівнює 2с.
Означення
3.
Точки перетину еліпса з осями координат
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() називаються
вершинами.
називаються
вершинами.
Означення
4.
Відрізки![]() ,
,
![]() називаються осями
еліпса.
називаються осями
еліпса.
Означення
5.
Форма еліпса (міра його стиску)
характеризується його ексцентриситетом,
рівним
відношенню відстані (2с)
між
фокусами до великої осі
![]()
![]()
Означення
6.
Відстані
![]() і
і
![]() деякої точки еліпса
деякої точки еліпса
![]() до його фокусів називаються фокальними
радіусами-векторами
цієї точки, причому
до його фокусів називаються фокальними
радіусами-векторами
цієї точки, причому
![]() (сума
фокальних
радіусів-векторів будь-якої точки еліпса
дорівнює
його більшій осі), і визначаються
формулами:
(сума
фокальних
радіусів-векторів будь-якої точки еліпса
дорівнює
його більшій осі), і визначаються
формулами:
![]() (правий
фокальний радіус-вектор),
(правий
фокальний радіус-вектор),
![]() (лівий
фокальний радіус-вектор).
(лівий
фокальний радіус-вектор).
В
окремому випадку, коли
![]() фокуси
зливаються
в одній точці - центрі, еліпс перетворюється
в коло з рівнянням
фокуси
зливаються
в одній точці - центрі, еліпс перетворюється
в коло з рівнянням
![]()
Взаємне
розташування точки
![]() і
еліпса
і
еліпса
![]() визначається
такими умовами:
визначається
такими умовами:
1)якщо![]() ,
то точка М
лежить
на еліпсі:
,
то точка М
лежить
на еліпсі:
2)якщо
![]() ,
то точка М
лежить
за межами еліпса;
,
то точка М
лежить
за межами еліпса;
3)якщо![]() ,
то точка М
лежить
всередині еліпса.
,
то точка М
лежить
всередині еліпса.
Означення
7.
Директрисами
еліпса
називаються дві прямі
![]() і
і
![]() ,
паралельні
малій осі і віддалені від неї на відстані,
рівній
,
паралельні
малій осі і віддалені від неї на відстані,
рівній
![]()
Їх рівняння мають вигляд:
![]() і
і
![]() ,
або
,
або
![]() ,
,
![]()
Відношення відстаней будь-якої точки еліпса до фокуса і відповідної директриси є величина постійна, рівна ексцентриситету еліпса:
![]() і
і
![]()
Таким чином, еліпс може бути визначений як геометричне місце точок, відношення відстаней яких від даної точки і даної прямої є величина постійна, менша одиниці.
Рівняння еліпса з осями, паралельними координатним осям, має вигляд:
![]() ,
де
,
де
![]() координати
центра елшса.
координати
центра елшса.
Еліпс має з будь-якою прямою дві точки перетину (дійсні, мнимі або ті, які співпадають).
Означення 8. Якщо пряма перетинає еліпс в двох точках, які співпадають, то вона називається дотичною до еліпса.
Рівняння
дотичної до
еліпса
![]() в точці
в точці
![]() має
має
вигляд:
![]()
З будь-якої точки можна провести до еліпса дві дотичні. Якщо точка лежить за межами еліпса, обидві дотичні дійсні; якщо точка лежить на еліпсі, дотичні співпадають; якщо точка лежить всередині еліпса, обидві дотичні уявні.
