Питання для самоперевірки

1. Запишіть загальне рівняння площини і дайте геометричне пояснення коефіцієнтів при змінних у цьому рівнянні.

2. Вкажіть на особливості в розміщенні площин, які задані неповними рівняннями:

а) ; в) ; д) ;

б) ; г) ; е) .

3. Запишіть рівняння площини у відрізках і дайте геометричне пояснення коефіцієнтів у цьому рівнянні.

4. За допомогою яких алгебраїчних перетворень із загального рівняння площини можна дістати рівняння площини у відрізках?

5. Запишіть рівняння площини, що проходить через три дані точки. Яка властивість компланарних векторів використовується при одержанні цього рівняння?

6. Запишіть нормальне рівняння площини і дайте геометричне пояснення коефіцієнтів при змінних і вільному члену в ньому рівнянні.

7. Сформулюйте правило, за яким загальне рівняння площини приводиться до нормального вигляду.

8. Що називається відстанню від точки до площини і за яким правилом вона обчислюється?

9. Запишіть формулу косинуса кута між двома площинами. За допомогою яких міркувань із цієї формули одержуються умови паралельності, перпендикулярності двох площин?

10. В чому полягає геометричний зміст знаку многочлена ?

11. Що називається пучком площин?

РОЗДІЛ 2. Аудиторні практичні заняття

Підмодуль 1. Складання рівняння площини. Геометричний зміст знаку многочлена. Неповні рівняння площини.

Питання для перевірки теоретичних знань:

1. Загальне рівняння площини має вигляд: ...

2. Рівняння площини, що проходить через три задані точки, має вигляд: ...

3. Запишіть рівняння площини у відрізках на осях.

4. Сформулюйте умову паралельності вектора і площини.

5. Для яких точок простору знак многочлена більше нуля, а для яких менше?

Завдання для аудиторної роботи

Приклад 1. Чи проходить площина через точки ?

Розв’язання. У загальне рівняння площини підставимо координати точки. Якщо рівність виконується, то площина проходить через точку, якщо ні — то не проходить. Отже, площина проходить через точки А, В і С та не проходить через точку D.

Приклад 2. Які особливості в розміщенні площин: 1); 2); 3); 4); 5)?

Розв’язання. 1) проходить паралельно осі OZ; 2) проходить через початок координат O(0; 0; 0;); 3) проходить паралельно площині ОXZ; 4) проходить паралельно осі ОY; 5) проходить через вісь ОX.

Приклад 3. Дано дві точки і . Скласти рівняння площини, що проходить через точку перпендикулярно вектору .

Розв’язання. ; за умовою перпендикулярності двох векторів маємо або .

Приклад 4. Скласти рівняння площини, що проходить:

1) через точки паралельно осі ОХ.

Розв’язання. Запишемо рівняння площини, що проходить через точки .

Для того, щоб написати рівняння площини, достатньо знати координати двох неколінеарних векторів, паралельних площині. За один з таких векторів можна прийняти координатний вектор , а за інший – вектор . Очевидно, , . Якщо прийняти за початкову точку, то рівняння площини прийме вигляд:

або

Таким чином, дана площина має рівняння:

2) через вісь ОХ і точку

Відповідь:

3) через точку паралельно площині OXY

Відповідь:

Приклад 5. Скласти рівняння площини, що проходить:

1) через точки паралельно вектору (3;0;1)

Відповідь:

2) через точку паралельно векторам і .

Розв’язання. Рівняння даної площини буде мати вигляд

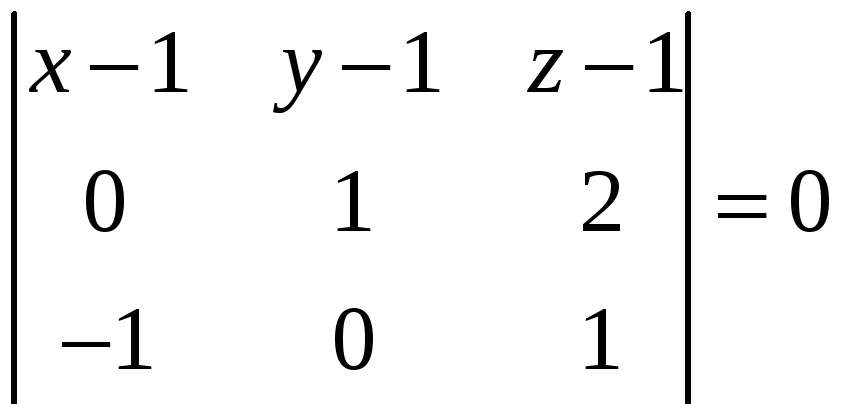або .

3) через три задані точки .

Розв’язання. За формулою маємо

;

Таким чином, дана площина має вигляд

.

Приклад 6. Скласти рівняння площини, що відтинає на осях ОY i OZ удвічі більші відрізки, ніж на осі ОХ, і проходить через точку .

Розв’язання. Рівняння площини у відрізках:

.

Оскільки площина проходить через точку , то .

Отже , а рівняння має вигляд .

Рівняння площини, що проходить через точку : .

Приклад 7. Дано точки

і площини

1. ;

2. .

Для кожної з площин серед даних точок вказати ті, які лежать по ту ж сторону від площини, що і початок координат.

1. Розв’язання.

Щоб визначити, чи лежать 2 точки по одну і ту саму сторону від заданої площини, необхідно визначити знаки многочлена для обох точок та порівняти їх. Таким чином, для точки , для точки . Отже, початок координат та точка лежать по одну сторону від площини .

Аналогічно визначаємо, що по ту ж сторону від заданої площини, що і початок координат, знаходяться точки .

2. Відповідь: .

Приклад 8. Перевірити, чи можна провести площину через такі чотири точки , , , .

Відповідь: ні.

Приклад 9. Дано вершини тетраедра , , і . Написати рівняння площини, що проходить через ребро і паралельна ребру ;

Розв’язання.

Щоб знайти задане рівняння, необхідно знайти координати векторів і . Маємо, , . Для довільної точки , що належить шуканій площині, вектори , і повинні задовольняти умові компланарності векторів, тому

. Звідси шукане рівняння має вигляд

.

Домашнє завдання

Приклад 1. Знайти рівняння площини, що проходить через точку і паралельна векторам і .

Відповідь:

Приклад 2. Знайти рівняння площини, що проходить через точки , і паралельна вектору .

Відповідь:

Приклад 3. Знайти рівняння площини, що проходить через точки

Відповідь: .

Приклад 4. Дано вершини тетраедра , , та . Написати рівняння площини, що проходить через вершину А і паралельна грані .

Відповідь: .

Приклад 5. Скласти рівняння площини, що проходить через точки і паралельно осі .

Відповідь: .

Приклад 6. Скласти рівняння площини, що проходить через вісь і точку .

Відповідь: .

Приклад 7. Скласти рівняння площини, що проходить через точку і відтинає від осей координат рівні відрізки.

Відповідь: , , .

Приклад 8. Скласти рівняння площини, яка проходить через початок координат перпендикулярно до двох площин , .

Відповідь: .

Приклад 9. Знайти точки перетину площини з координатними осями.

Відповідь: .

Приклад 10. Обчислити об’єм піраміди, обмеженої площиною і координатними площинами.

Відповідь: 8.

Приклад 11. Дана площина . Вказати, які з пар точок, наведених нижче, лежать по одну і ту ж сторону від даної площини:

а) і ;

б) і ;

в) і .

Відповідь: а) і в).

Підмодуль 2. Нормальне рівняння площини. Відстань від точки до площини. Взаємне розташування площин. Кут між площинами. Пучок площин.

Питання для перевірки теоретичних знань

1. Як привести загальне рівняння площини до нормального виду?

2. Перерахуйте способи розташування двох і трьох площин.

3. Назвіть формулу, за якою обчислюється кут між площинами.

4. Сформулюйте умови паралельності і перпендикулярності площин.

Завдання для аудиторної роботи

Приклад 1. Написати нормальне рівняння площини, що задана рівнянням

а) .

Розв’язання.

Так як , то

Нормальне рівняння площини має вигляд

б)

Відповідь:

Приклад 2. Обчислити відстань між паралельними площинами та .

Розв’язання. Знайдемо точку, яка б належала площині . Наприклад, . Обчислимо відстань від цієї точки до іншої площини, беручи до уваги, що нормуючий множник :

Приклад 3. Скласти рівняння площини, що проходить через точку :

1. паралельно площині .

Розв’язання. За умовою паралельності площин 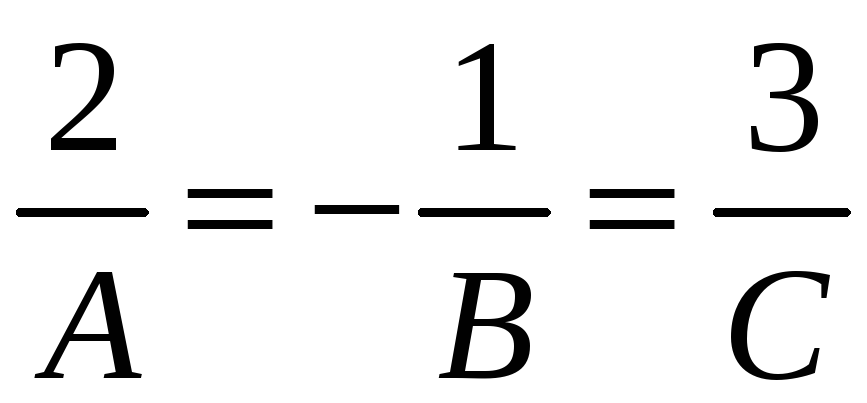, тобто рівняння площини має вигляд . Оскільки точка належить шуканій площині, то , .

Отже, .

2. перпендикулярно площинам і .

Розв’язання. Оскільки задані площини перпендикулярні шуканій площині, то їх нормальні вектори будуть паралельні їй. Тому вектори , і – компланарні, звідси

, ,

Приклад 4. На осі знайти точку, рівновіддалену від площин і .

Розв’язання. Точка має вигляд . Запишемо відстані від площин до точки і прирівняємо їх:

; ;

1. ; ; ; або

2. ; ; ; .

Приклад 5. Обчислити косинус кута між площинами ; .

Розв’язання. За формулою для обчислення косинуса кута між площинами (див. Розділ 1) маємо:

Приклад 6. Скласти рівняння дотичної площини до сфери в точці .

Розв’язання. Оскільки радіус сфери перпендикулярний до дотичної площини, то виконується умова перпендикулярності векторів і :

.

Приклад 7. Визначити, початок координат лежить всередині тупого чи гострого кута, утвореного двома площинами і .

Розв’язання. Визначимо косинус кута між нормальними векторами цих площин:

, отже, кут між і гострий. Тоді точки, що лежать всередині гострого кута будуть мати різні знаки многочлена по відношенню до даних площин, а точки, що лежать всередині тупого кута, – однакові.

Перевіримо знаки многочленів для точки :

.

Знаки різні, тому початок координат лежить всередині гострого кута між даними площинами.

Приклад 8. Написати рівняння площин, що ділять навпіл двогранні кути між площинами і .

Відповідь: ,

Приклад 9. Знайти відстань від точки до площини .

Відповідь: 1

Приклад 10. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 3.

Розв’язання. Шукані множини точок належать площинам, що паралельні даній і знаходяться на відстані 3 від неї, тому

. Звідси отримаємо дві площини, які задовольняють умові: і .

Домашнє завдання

Приклад 1. Привести до нормального виду рівняння площин:

1. ;

Відповідь:

2. .

Відповідь: .

Приклад 2. Обчислити відстань між паралельними площинами

1. ,

Відповідь: ;

2. ;

Відповідь: .

Приклад 3. Дві грані куба лежать на площинах , . Обчислити об’єм даного куба.

Відповідь: .

Приклад 4. На осі знайти точку, рівновіддалену від двох площин , .

Відповідь: і .

Приклад 5. Написати рівняння площини, що проходить через точку перпендикулярно до площин і .

Відповідь: .

Приклад 6. Скласти рівняння дотичної площини до сфери в точці .

Відповідь:

Приклад 7. Визначити, чи лежить точка всередині гострого чи тупого кута, утвореного двома площинами , .

Відповідь: Всередині тупого кута.

Приклад 8. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 3.

Відповідь: і .

Приклад 9. Написати рівняння сфери, центр якої лежить на осі і яка дотикається до двох площин і .

Відповідь: .

РОЗДІЛ 3. Індивідуальне завдання до модуля «Площина в просторі»

ВАРІАНТ №1

1. Скласти рівняння площини, що проходить через 3 точки А(1; 0; -2), В(2; 1; -1), С(0; 2; -3). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (0; 0; -1), (1; 3; 4), (5; 0; -3), (4; 4; 1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 3; 1), М₂(1; -5; 2).

4. Скласти рівняння площини, що проходить через точку А(1; 2; 5) і вісь ОХ.

5. Написати рівняння площини, що проходить через точку М₁(4; 3; -1) перпендикулярно вектору (1; 3; 2).

6. Дано тетраедр АВСD з вершинами А(1; 0; 1), В(3; 1; -5), С(-2; ; 2), D(-1; 1; 1). Знайти кут між гранями АВС і АDС.

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OZ знайти точку, рівновіддалену від точки М(2; 1; 1) та від площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані 3 см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і 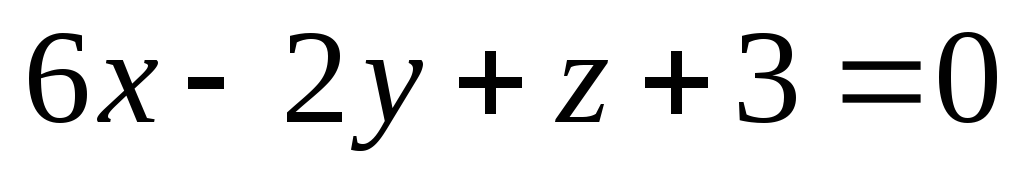, в якому лежить точка М(1; 2; -4).

ВАРІАНТ №2

1. Скласти рівняння площини, що проходить через 3 точки А(3; 3; 1), В(2; -1; 2), С(-5; 1; 1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (3; 2; 1), (-5; -5; 0), (1; 4; 3), (7; 3 0) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(0; 1; 7), М₂(3; -2; 4).

4. Скласти рівняння площини, що проходить через 2 точки А(1; 2; 0) та В(-3; 1; 4) і паралельна вектору (2; 0; -1).

5. Написати рівняння площини, що проходить через точку М₁(2; -1; 5) перпендикулярно вектору (4; 1; -2).

6. Дано тетраедр АВСD з вершинами А(-3; 0; 1), В(3; -2; -4), С(1; 1; 0), D(-2; -2; 1). Знайти кут між гранями ABC i ABD.

7. Тетраедр АВСD задано його вершинами А(1; 0; 1), В(-3; -1; 7), С(2; 3; 5), D(4; 3; 10). Знайти довжину висоти DH.

8. На осі OY знайти точку, рівновіддалену від двох площин і .

9. Скласти рівняння множини точок, що відстоять від площини на відстані 4 см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; 0; -3).

ВАРІАНТ №3

1. Скласти рівняння площини, що проходить через 3 точки А(1; 4; 1), В(-3; 6; 2), С(2; -10; 3). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (6; -1; 2), (3; 5; -2), (4; -3; 0), (2; -3; 1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-2; 1; 2), М₂(4; -1; 3).

4. Скласти рівняння площини, що проходить через точку А(-5;1; 8) і паралельна двом векторам (2; -5; 0) та (4; 3; -2).

5. Написати рівняння площини, що проходить через точку М₁(-3; 0; 2) перпендикулярно вектору (-4; 2; 0).

6. Площина задана трьома точками А(2; 1; 6), В(-3; 2; 1), С(4; -1; 0), а площина – точками (-7; 1; 2), (0; -3; -1), (-5; 2; 2). Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OХ знайти точку, рівновіддалену від двох площин і .

9. Скласти рівняння множини точок, що відстоять від площини на відстані см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; -3; 1).

ВАРІАНТ №4

1. Скласти рівняння площини, що проходить через 3 точки А(2; 4; 3), В(1; -3; 9), С(-3; 1; 1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (3; 6; 0), (5; 4; 3), (4; -2; 2), (3; 3; 5) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 4; 1), М₂(-3; 1; 6).

4. Написати рівняння площини, що проходить через 2 точки А(1; 8; 6), В(3; 7; -4) та перпендикулярна площині .

5. Написати рівняння площини, що проходить через точку М₁(1; 2; -2) перпендикулярно вектору (3; -2; -7).

6. Дано тетраедр АВСD з вершинами А(1; 0; 1), В(3; 1; -5), С(-2; ; 2), D(-1; 1; 1). Знайти кут між гранями АВD і АDС.

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від точки М(2; 1; 1) та від площини .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та .

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-4; 2; 1).

ВАРІАНТ №5

1. Скласти рівняння площини, що проходить через 3 точки А(2; 4; -2), В(1; -3; -1), С(4; 3; -1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-3; 0; 4), (1; 2; -6), (0; -2; -7), (-4; -4; 3) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(1; -3; 5), М₂(0; 7; 2).

4. Скласти рівняння площини, що проходить через точку А(1; 2; 5) і вісь ОY.

5. Написати рівняння площини, що проходить через точку М₁(5; 4; 1) перпендикулярно вектору (1; -3; -2).

6. Дано тетраедр АВСD з вершинами А(-3; 0; 1), В(3; -2; -4), С(1; 1; 0), D(-2; -2; 1). Знайти кут між гранями ABC i AСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OZ знайти точку, рівновіддалену від двох площин і .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та .

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-5; 4; -1)

ВАРІАНТ №6

1. Скласти рівняння площини, що проходить через 3 точки А(-1; -2; 1), В(3; 2; 0), С(2; 4; 1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2; 1; 0), (3; 2; 5), (-6; 1; 3), (1; -5; 1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; -1; 3), М₂(4; 2; 0).

4. Скласти рівняння площини, що проходить через початок координат і паралельна двом векторам (-1; 2; 3)та 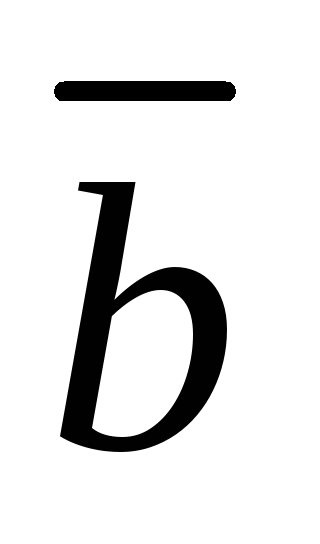(2; 1; -3).

5. Написати рівняння площини, що проходить через точку М₁(3; -3; 1) перпендикулярно вектору (2; 2; 5).

6. Площина задана трьома точками А(2; 3; -3), В(1; 2; -4), С(-3; -4; -4), а площина – точками (-4; 1; 3), (-3; -2; -2), (1; 0; -1). Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OХ знайти точку, рівновіддалену від точки М(1; 1; -1) та від площини .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та .

10. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами .

ВАРІАНТ №7

1. Скласти рівняння площини, що проходить через 3 точки А(1; 3; 1), В(5; 4; 8), С(2; -1; 7). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (4; -4; 1), (2; -7; 2), (1; 3; 2), (2; 4; 5) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-3; 2; 3), М₂(2; 4; -1).

4. Скласти рівняння площини, що проходить через 2 точки А(2; -3; 1), В(3; 2; 3) та перпендикулярна площині

5. Написати рівняння площини, що проходить через точку М₁(-1; -1; 2) перпендикулярно вектору (5; 3; -4).

6. Дано тетраедр АВСD з вершинами А(1; 0; 1), В(3; 1; -5), С(-2; ; 2), D(-1; 1; 1). Знайти кут між гранями BCD і АBD.

6. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

6. На осі OZ знайти точку, рівновіддалену від двох площин та .

6. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 5 см.

6. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

ВАРІАНТ №8

1. Скласти рівняння площини, що проходить через 3 точки А(2; 5; -4), В(-1; 2; 2), С(0; -2; -5). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1; -1; 2), (2; -3; -5), (7; 2; 4), (-3; 0; 6) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(1; -2; 1), М₂(-3; -3; 1).

4. Скласти рівняння площини, що проходить через точку А(1; 2; 5) та вісь ОZ.

5. Написати рівняння площини, що проходить через точку М₁(-2; 3; -2) перпендикулярно вектору (-3; -1; 4).

6. Дано тетраедр АВСD з вершинами А(-3; 0; 1), В(3; -2; -4), С(1; 1; 0), D(-2; -2; 1). Знайти кут між гранями ABD i AСD.

6. Тетраедр АВСD задано його вершинами А(1; 2; 1), В(4; -2; -2), С(-2; 0; 1), D(-4; -1; 0). Знайти довжину висоти DH.

6. На осі OХ знайти точку, рівновіддалену від точки М(2; -1; -2) та площини .

6. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин 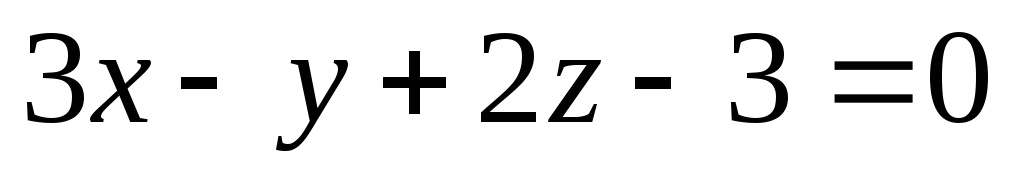та .

6. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами

ВАРІАНТ №9

1. Скласти рівняння площини, що проходить через 3 точки А(3; 5; -15), В(0; 4; -3), С(-2; 1; -2). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1; -2; 4), (2; 0; -1), (5; -3; 2), (3; 1; -4) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-3; -1; 4), М₂(1; 4; 0).

4. Скласти рівняння площини, що проходить через 2 точки А(6; 1; 3) та В(-5; 2; -1) і паралельна вектору осі ОХ.

5. Написати рівняння площини, що проходить через точку М₁(-5; -1; -3) перпендикулярно вектору 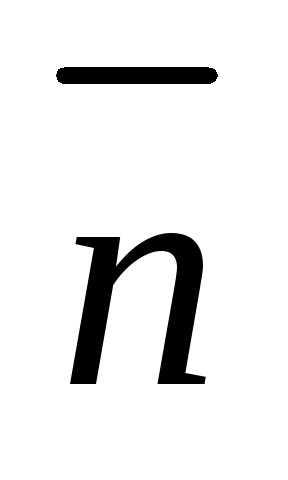(2; 0; -3).

6. Площина задана трьома точками А(-2; 1; 1), В(3; -2; 4), С(0; -1; -1), а площина – точками (1; 5; 1), (2; -3; -3), (3; 4; -2). Знайти кут між площинами і .

6. Знайти відстань між паралельними площинами

.

6. На осі OY знайти точку, рівновіддалену від точки М(1; 1; -3) та площини .

6. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 2 см.

6. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

ВАРІАНТ №10

1. Скласти рівняння площини, що проходить через 3 точки А(-1; 2; 3), В(2; 0; 9), С(1; -4; 0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1; 1; 3), (2; 4; -5), (2; -3; 7), (0; -1; 3) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 1; 3), М₂(1; -1; 1).

4. Скласти рівняння площини, що проходить через 2 точки А(-3; 1; 8) та В(-4; -1; 1) і перпендикулярна площині YOZ.

5. Написати рівняння площини, що проходить через точку М₁(2; 3; -1) перпендикулярно вектору (6; -3; 5).

6. Дано тетраедр АВСD з вершинами А(1; 0; 1), В(3; 1; -5), С(-2; 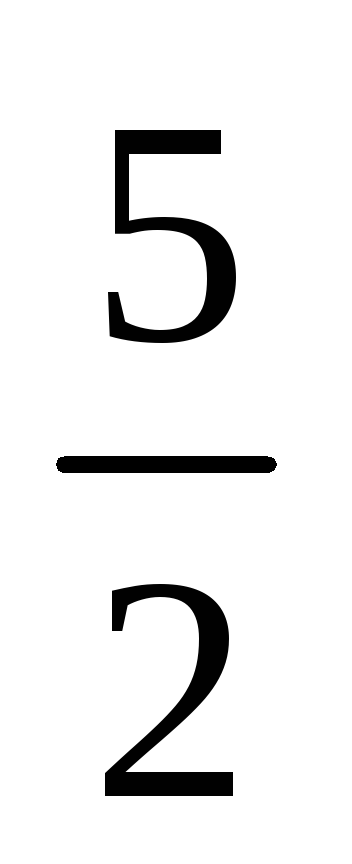; 2), D(-1; 1; 1). Знайти кут між гранями BCD і АСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від площин та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами .

ВАРІАНТ №11

1. Скласти рівняння площини, що проходить через 3 точки A (-2;3;6), В(-3;1;-4), С(1;-2;3). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2;-2;1), (3;0;-1), (1;3;2), (-3;1;-2) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-1; 3; 1), М₂(2; -2; 3).

4. Скласти рівняння площини, що проходить через 2 точки А(6; 1; 3) та В(-5; 2; -1) і паралельна осі OY.

5. Написати рівняння площини, що проходить через точку М₁(2; -2; -1) перпендикулярно вектору (6; 2; 3).

6. Дано тетраедр АВСD з вершинами А(-3; 0; 1), В(3; -2; -4), С(1; 1; 0), D(-2; -2; 1). Знайти кут між гранями BCD i ABD.

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OZ знайти точку, рівновіддалену від площин та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(1; 2; -4).

ВАРІАНТ №12

1. Скласти рівняння площини, що проходить через 3 точки A (2;-1;-2), В(-3;2;-4), С(-1;0;2). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-1; 3;1), (2;-1;2), (-2; 2;0), (3;2;1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 0; -1), М₂(1; 3; 2).

4. Скласти рівняння площини, що проходить через 2 точки А(-3; 1; 8) та В(-4; -1; 1) і паралельна площині XOZ.

5. Написати рівняння площини, що проходить через точку М₁(-2; 0; -3) перпендикулярно вектору (4; 3; -1).

6. Площина задана трьома точками А(1; -1; 2), В(3; 5; 3), С(-2; -4; -1), а площина – точками (-4; 3; 1), (1; -2; -2), (-8; 1; -3). Знайти кут між площинами і .

7. Тетраедр АВСD задано його вершинами А(3; -1; 0), В(1; 1; ), С(-2; 3; ), D(2; 1; 4). Знайти довжину висоти DH.

8. На осі OX знайти точку, рівновіддалену від площин та .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; 0; -3).

ВАРІАНТ №13

1. Скласти рівняння площини, що проходить через 3 точки A (1;0;1), В(0;2;-1), С(-2;2;-2). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1;2;1), (-3;-2;-3), ( 2;0;1), (-1;-3;-2) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(3; 3; 1), М₂(2; -1; 2).

4. Скласти рівняння площини, що проходить через 2 точки А(6; 1; 3) та В(-5; 2; -1) і паралельна осі OZ.

5. Написати рівняння площини, що проходить через точку М₁(2; -1; 3) перпендикулярно вектору (-1; 3; 4).

6. Дано тетраедр АВСD з вершинами А(-3; 0; 1), В(3; -2; -4), С(1; 1; 0), D(-2; -2; 1). Знайти кут між гранями ABC i BСD.

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OY знайти точку, рівновіддалену від точки М(-1; 2; 1) і площини .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; -3; 1).

ВАРІАНТ №14

1. Скласти рівняння площини, що проходить через 3 точки A (3;-1;1), В(-4;3;0), С(2;-6;-1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (4;2;1), (-2;0;3), (3;1; 2), (2;-1;-1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-2; 1; 2), М₂(1; 2; -3).

4. Скласти рівняння площини, що проходить через 2 точки А(-3; 1; 8) та В(-4; -1; 1) і перпендикулярна площині XOY.

5. Написати рівняння площини, що проходить через точку М₁( -2; 3; 4) перпендикулярно вектору (3; -1; 5).

6. Задано точки 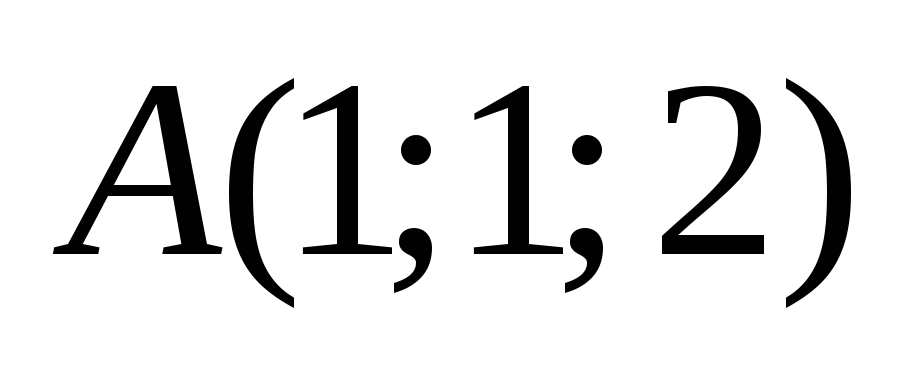, , , , , 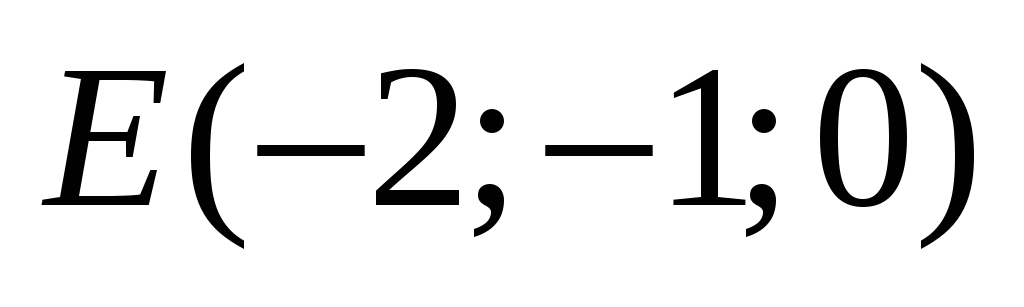. Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OZ знайти точку, рівновіддалену від точки М(2; 0; -1) і площини .

9. Скласти рівняння множини точок, що відстоять від площини 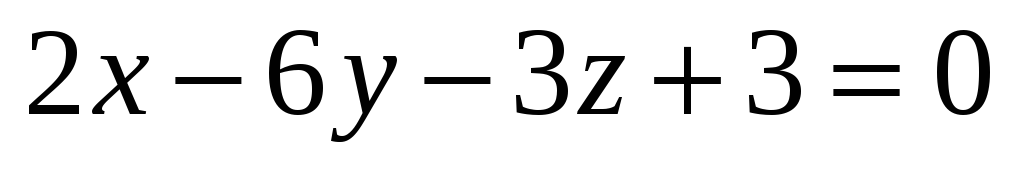на відстані, що дорівнює 2 см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-4; 2; 1).

ВАРІАНТ №15

1. Скласти рівняння площини, що проходить через 3 точки A (-1;-2;2), В(1;1;-5), С(2;5;-6). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2;1; 4), (-1;3;3), (3;-3;3), (-5;0;-4) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(1; 2; 1), М₂(3; -2; 1).

4. Скласти рівняння площини, що проходить через точку А(-3; 4; 1) та вісь ОХ.

5. Написати рівняння площини, що проходить через точку М₁(-1; 3; -4) перпендикулярно вектору (2; 0; -3).

6. Задано точки , , , , . Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OX знайти точку, рівновіддалену від площин 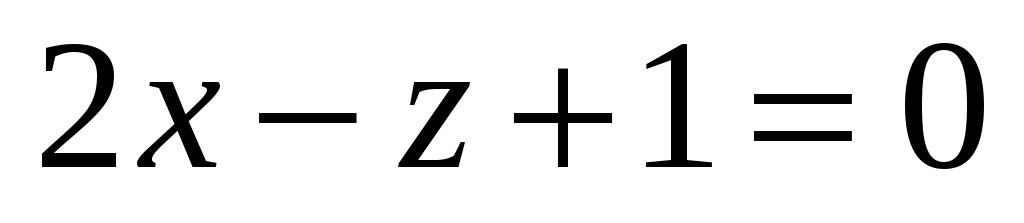та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-5; 4; -1).

ВАРІАНТ №16

1. Скласти рівняння площини, що проходить через 3 точки A (1;-1;4), В(-3;5;1), С(3;-4;-2). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (4;-1; -3), (2;1;2), (1;4;-2), (3;-1;1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 1; -2), М₂(3; 2; -4).

4. Скласти рівняння площини, що проходить через 2 точки А(2; 0; -3) та В(-1; -2; -4) і паралельна вектору (1; 3; -1).

5. Написати рівняння площини, що проходить через точку М₁(2; -1; 1) перпендикулярно вектору (4; 2; 1).

6. Задано точки 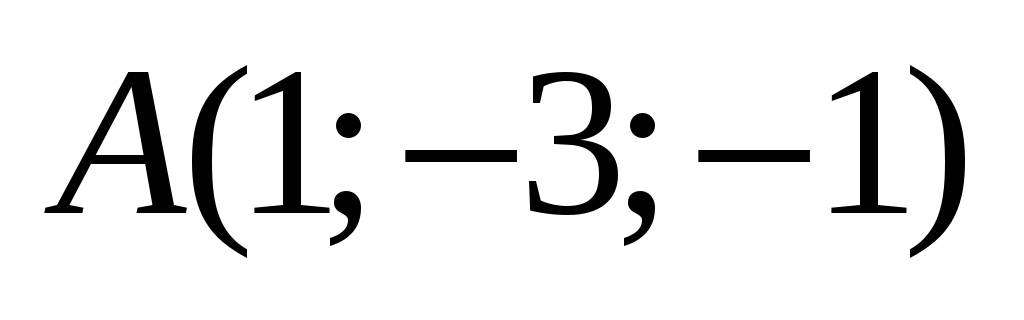, , , , . Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від точки М(2; 1; 0) і площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 4 см.

10. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами .

ВАРІАНТ №17

1. Скласти рівняння площини, що проходить через 3 точки A (1;0;-3), В(-2;-5;4), С(-1;-2;3). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1;1;2), (2;-3;1), (4;-1;-2), (-2;3;-1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(1; 0; 4), М₂(-2; 1; 4).

4. Скласти рівняння площини, що проходить через точку А(3; 2; -1) і паралельна двом векторам (2; 1; 4) та (3; 0; -2).

5. Написати рівняння площини, що проходить через точку М₁(-3; 2; 1) перпендикулярно вектору (1; -3; 4).

6. Задано точки , , , , . Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OZ знайти точку, рівновіддалену від площин та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та .

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

ВАРІАНТ №18

1. Скласти рівняння площини, що проходить через 3 точки A (2;-3;1), В(-1;6;2), С(-2;2;0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-3;2;2), (4;1;-1), (2;-3;1), (1;0;-2) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 1; -3), М₂(-1; -1; 1).

4. Скласти рівняння площини, що проходить через 2 точки А(4; 2; 1) та В(2; 0; -1) і паралельна площині .

5. Написати рівняння площини, що проходить через точку М₁(1; 4; 0) перпендикулярно вектору (-3; 2; 2).

6. Дано тетраедр з вершинами , , , . Знайти кут між площинами і .

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OX знайти точку, рівновіддалену від точки М(1; -3; 1) і площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 3 см.

10. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами

ВАРІАНТ №19

1. Скласти рівняння площини, що проходить через 3 точки A (1;2;3), В(3;0;3), С(-2;3;0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (4;-1;6), (-3;-2;0), (2; 1;2), (-1;2;-2) одній площині.

3. З’ясувати, чи перетинає площина 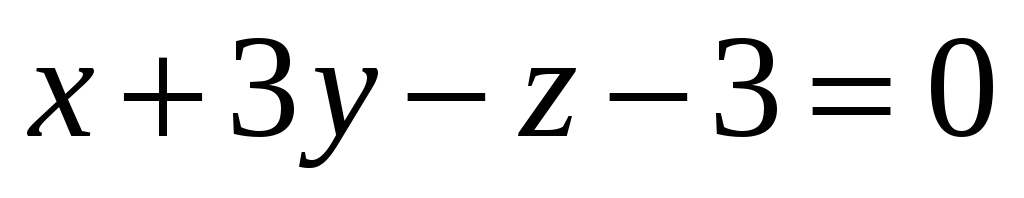відрізок, обмежений точками М₁(4; -1; 3), М₂(3; 0; 1).

4. Скласти рівняння площини, що проходить через початок координат і паралельна двом векторам (2; 1; -3) та (-1; 3; -1).

5. Написати рівняння площини, що проходить через точку М₁(2; -3; -1) перпендикулярно вектору (4; 1; -3).

6. Дано тетраедр з вершинами 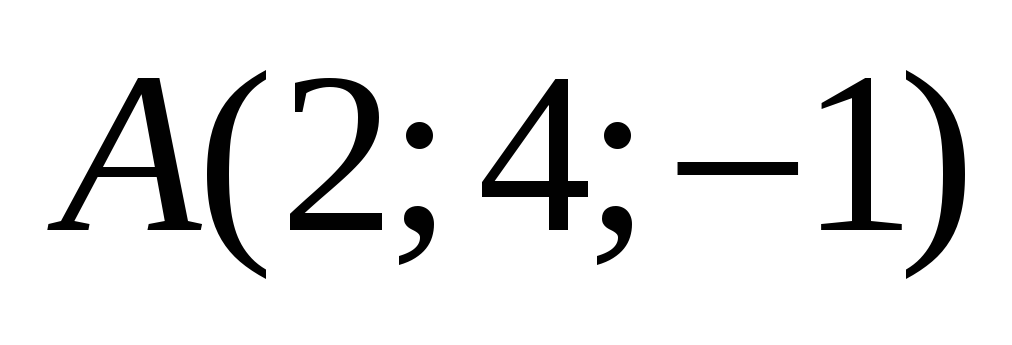, , , . Знайти кут між площинами і .

7. Тетраедр АВСD задано його вершинами А(2; -3; 1), В(0; -5; -2), С(1; 1; 2), D(2; -1; 3). Знайти довжину висоти DH.

8. На осі OY знайти точку, рівновіддалену від площин та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

ВАРІАНТ №20

1. Скласти рівняння площини, що проходить через 3 точки A (1;-2;-4), В(3;0;1), С(-1;1;1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-3;1;4), (2;0;-1), (-1;2;3), (4;2;-5) одній площині.

3. З’ясувати, чи перетинає площина 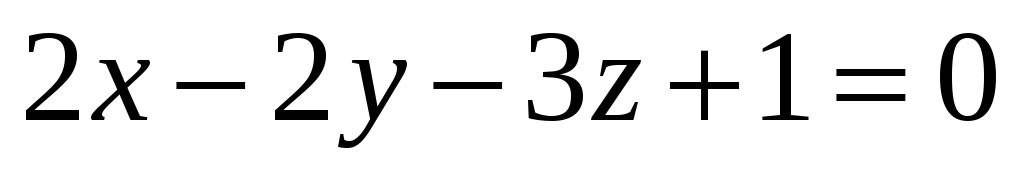відрізок, обмежений точками М₁(3; 1; 1), М₂(-2; 4; 0).

4. Скласти рівняння площини, що проходить через 2 точки A (2; -1; 3), В(-2; 2; 1) та паралельна осі ОХ.

5. Написати рівняння площини, що проходить через точку М₁(4; 1; -2) перпендикулярно вектору (3; -5; 2).

6. Дано тетраедр з вершинами , , , . Знайти кут між площинами і .

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OZ знайти точку, рівновіддалену від точки М(1; -1; 1) і площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 2 см.

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами .

ВАРІАНТ №21

1. Скласти рівняння площини, що проходить через 3 точки A (3;1;-1), В(2;-1;-1), С(0;3;1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2;1;-1), (3;2;1), (1;-2; 2), (-3;0;4) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 2; -1), М₂(3; -1; 2).

4. Скласти рівняння площини, що проходить через 2 точки A (3; -2; 1), В(1; 3; 2) та перпендикулярна площині YOZ

5. Написати рівняння площини, що проходить через точку М₁(-1; 3; 4) перпендикулярно вектору (2; -1; 4).

6. Дано тетраедр з вершинами , , , . Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OX знайти точку, рівновіддалену від площин 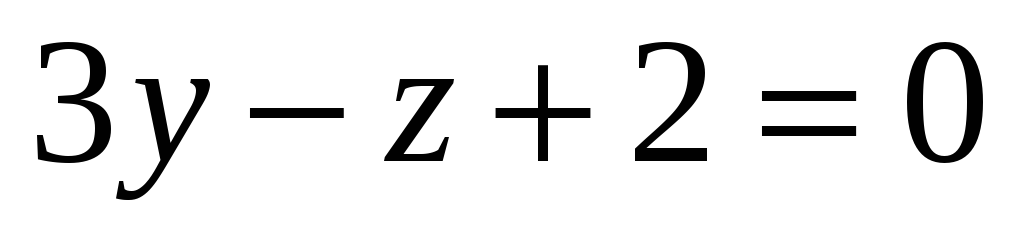та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(1; 2; -4).

ВАРІАНТ №22

1. Скласти рівняння площини, що проходить через 3 точки A (2;4;-4), В(-1;0;1), С(1;3;-2). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-2;-1; 3), (4;1;2), (3; 2;0), (1;3;1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(3; 2;0), М₂(4; 1; -3).

4. Скласти рівняння площини, що проходить через точку A (2; 1; -4), та вісь OY.

5. Написати рівняння площини, що проходить через точку М₁(-1; -3; 0) перпендикулярно вектору (3; -2; 1).

6. Дано тетраедр з вершинами , , , . Знайти кут між площинами і .

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від двох площин 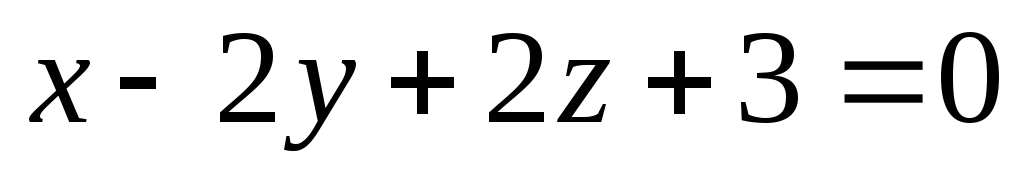і .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 3 см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; 0; -3).

ВАРІАНТ №23

1. Скласти рівняння площини, що проходить через 3 точки A (-2;1;-2), В(1;-2;-5), С(-4;-1;0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1;-2;2), (3;3;-1), (4;0;-6), (1;-3;-3) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-2; -1; 3), М₂(2; -2; -4).

4. Скласти рівняння площини, що проходить через 2 точки A (-2; 2; 3), В(1; -2; 1) та паралельна вектору (4; 0; -1).

5. Написати рівняння площини, що проходить через точку М₁(3; 1; 4) перпендикулярно вектору (1; 3; -2).

6. Дано 5 точок: A(2; 1; 1), B(-3; 4; -3), C(1; -2; -7), D(-1; -1; -1), E(-2; -5; 0). Знайти кут між площинами ABC і ADE.

7. Знайти відстань між паралельними площинами

.

8. На осі OХ знайти точку, рівновіддалену від двох площин і .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та .

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(2; -3; 1).

ВАРІАНТ №24

1. Скласти рівняння площини, що проходить через 3 точки A (2;-4;1), В(0;3;2), С(-1;2;1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (1;4;2), (-2;3;1), (3;-1;-1), (2;0;3) одній площині.

3. З’ясувати, чи перетинає площина 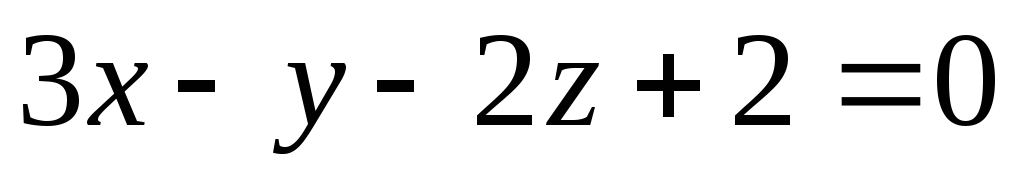відрізок, обмежений точками М₁(2; 1; -3), М₂(-3; 2; 1).

4. Скласти рівняння площини, що проходить через точку А(2; 1; 1) і паралельна двом векторам (3; 2; -2) і (1; -1; 4).

5. Написати рівняння площини, що проходить через точку М₁(4; 0; 3) перпендикулярно вектору (-2; 5; 1).

6. Дано 5 точок: A(2; 1; 1), B(-3; 4; -3), C(1; -2; -7), D(-1; -1; -1), E(-2; -5; 0). Знайти кут між площинами ACD і ADE.

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від точки М(2; 1; 1) та від площини .

9. Скласти рівняння множини точок, що відстоять від площини 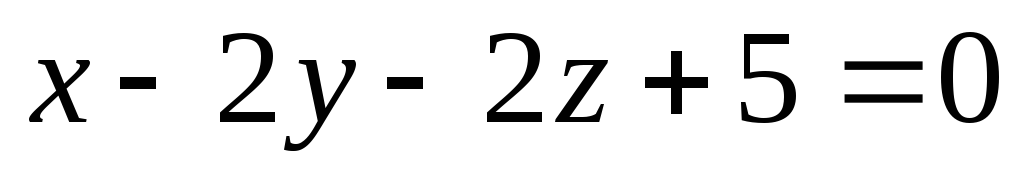на відстані, що дорівнює 4 см.

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-4; 2; 1).

ВАРІАНТ №25

1. Скласти рівняння площини, що проходить через 3 точки A (2;-1;-2), В(-1;0;2), С(1;1;6). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (3;1;0), (-2;-1;4), (1;3; 2), (2;0;-1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(4; -2; 4), М₂(2; -3; -1).

4. Скласти рівняння площини, що проходить через 2 точки A (-1; 3; 2), В(2; -2; 0) та перпендикулярна площині .

5. Написати рівняння площини, що проходить через точку М₁(-3; 2; -1) перпендикулярно вектору (1; 4; 5).

6. Дано тетраедр АВСD з вершинами А(3; 1; -4), В(2; -1; 3), С(1; 0; 4), D(-2; 3; 2). Знайти кут між гранями ABC i BСD.

7. Дано куб ABCDA₁B₁C₁D₁. Його паралельні грані належать площинам та . Знайти об’єм куба.

8. На осі OZ знайти точку, рівновіддалену від двох площин і .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин 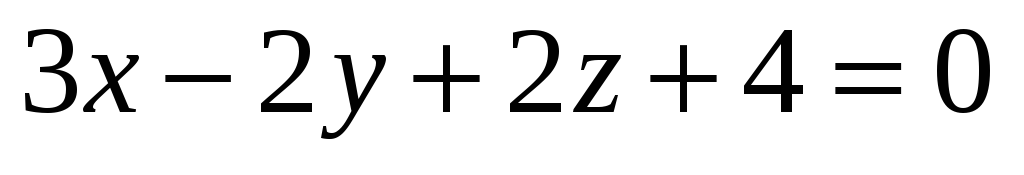та

10. Скласти рівняння площини, що ділить навпіл той двогранний кут між двома площинами і , в якому лежить точка М(-5; 4; -1)

ВАРІАНТ №26

1. Скласти рівняння площини, що проходить через 3 точки A (1;-1;-1), В(-2;1;-4), С(2;0;5). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2;0;-4), (-3;-1;-3), (1;1;1), (1;2;5) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(-3; 1; 4), М₂(1; 3; -3).

4. Скласти рівняння площини, що проходить через початок координат і паралельна двом векторам (4; -1; 3) і (-2; 1; 0).

5. Написати рівняння площини, що проходить через точку М₁(2; 4; 1) перпендикулярно вектору (-4; 1; 3).

6. Дано тетраедр АВСD з вершинами А(1; 0; -3), В(4; 1; 2), С(2; -2; 1), D(-1; 2; 3). Знайти кут між гранями ABC i BСD.

7. Тетраедр АВСD задано його вершинами А(1; 2; -1), В(-2; 0; -7), С(-1; 1; -6), D(3; -3; -4). Знайти довжину висоти DH.

8. На осі OХ знайти точку, рівновіддалену від точки М(1; 1; -1) та від площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 1 см.

10. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами .

ВАРІАНТ №27

1. Скласти рівняння площини, що проходить через 3 точки A (4;0;3), В(-2;2;3), С(1;-1;0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-1; 2;1), (3;-3;-2), (2;1;-1), (4;-2;0) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 1; -4), М₂(-3; -1; 2).

4. Скласти рівняння площини, що проходить через 2 точки А(2; 1; -3) і В(-3; -1; 1) та паралельна осі ОХ.

5. Написати рівняння площини, що проходить через точку М₁(2; -4; 1) перпендикулярно вектору (-3; 0; 5).

6. Дано тетраедр АВСD з вершинами А(1; 0; -3), В(4; 1; 2), С(2; -2; 1), D(-1; 2; 3). Знайти кут між гранями ABD i AСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OZ знайти точку, рівновіддалену від двох площин та .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

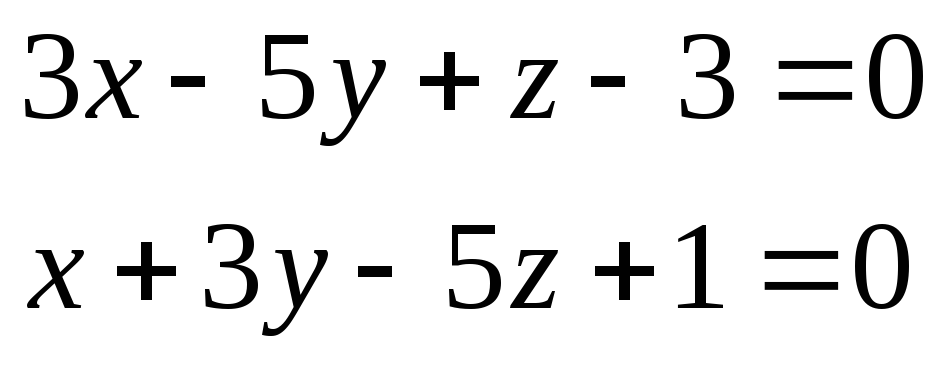
ВАРІАНТ №28

1. Скласти рівняння площини, що проходить через 3 точки A (-2;-1;0), В(-1;1;4), С(2;2;1). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-2; 2;3), (1;1;-2), (3;-1;1), (2;-2;-3) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(3; 1; -2), М₂(-2; 2; 2).

4. Скласти рівняння площини, що проходить через 2 точки А(5; 1; -2) і В(-1; 2; 4) та паралельна площині XOY.

5. Написати рівняння площини, що проходить через точку М₁(1; 2; 3) перпендикулярно вектору (4; -1; 2).

6. Дано тетраедр АВСD з вершинами А(1; -4; -1), В(2; -2; 0), С(-1; 1; 3), D(-2; -1; 4). Знайти кут між гранями ABC i BСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OХ знайти точку, рівновіддалену від точки М(2; -1; -2) та площини .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 2 см.

10. Скласти рівняння площини, що ділить навпіл тупий двогранний кут, утворений двома площинами

ВАРІАНТ №29

1. Скласти рівняння площини, що проходить через 3 точки A (1;2;3), В(2;3;4), С(-2;2;4). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (2;1;0), (-1;-2;-6), (-4;0;3), (3;1;-1) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(2; 0; 3), М₂(3; 1; -2).

4. Скласти рівняння площини, що проходить через точку А(6; 2; -3) і вісь OZ.

5. Написати рівняння площини, що проходить через точку М₁(-3; 1; 2) перпендикулярно вектору (2; 3; 4).

6. Дано тетраедр АВСD з вершинами А(1; -4; -1), В(2; -2; 0), С(-1; 1; 3), D(-2; -1; 4). Знайти кут між гранями ACD i BСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від точки М(1; 1; -3) та площини .

9. Скласти рівняння множини точок, рівновіддалених від двох паралельних площин та

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами

ВАРІАНТ №30

1. Скласти рівняння площини, що проходить через 3 точки A (2;2;1), В(-3;-1;2), С(1;1;0). Які відрізки відтинає ця площина на осях координат?

2. Перевірити, чи належать точки (-3;-2;1), (2;1;4), (1;-3; 2), (4;-1;3) одній площині.

3. З’ясувати, чи перетинає площина відрізок, обмежений точками М₁(3; 0; 1), М₂(-3; 1; 4).

4. Скласти рівняння площини, що проходить через 2 точки A(2; -1; 1) i В(5; 0; 2) та перпендикулярна площині XOZ.

5. Написати рівняння площини, що проходить через точку М₁(3; -1; 2) перпендикулярно вектору (-1; -2; -1).

6. Дано тетраедр АВСD з вершинами А(1; -4; -1), В(2; -2; 0), С(-1; 1; 3), D(-2; -1; 4). Знайти кут між гранями ABD i BСD.

7. Знайти відстань між паралельними площинами

.

8. На осі OY знайти точку, рівновіддалену від площин 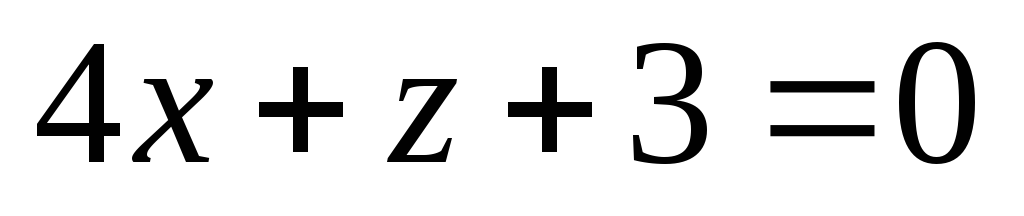та .

9. Скласти рівняння множини точок, що відстоять від площини на відстані, що дорівнює 3 см.

10. Скласти рівняння площини, що ділить навпіл гострий двогранний кут, утворений двома площинами .