
- •Розділ 1. Теоретичні відомості до модуля «Площина в просторі» Поняття площини та її рівняння
- •Способи задання площини
- •Умова паралельності вектора і площини
- •Дослідження загального рівняння площини
- •Геометричний зміст знаку многочлена
- •Нормальне рівняння площини
- •Відстань від точки до площини
- •Взаємне розташування двох площин в просторі
- •Взаємне розташування трьох площин в просторі
- •Кут між двома площинами
- •Пучок площин
- •Питання для самоперевірки
- •Підмодуль 1. Складання рівняння площини. Геометричний зміст знаку многочлена. Неповні рівняння площини.
- •Список літератури
Нормальне рівняння площини
Нормальне рівняння площини має вигляд:
![]() (9)
(9)
У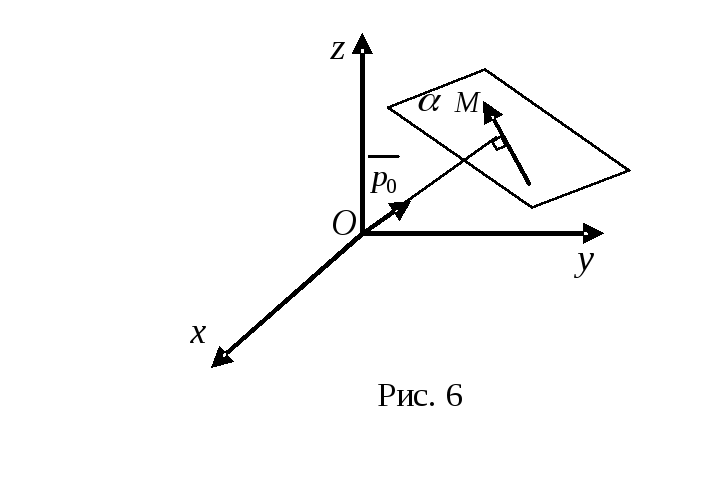 рівнянні (9)
рівнянні (9)
![]() – координати одиничного вектора, який
проведено із початку координат
перпендикулярно до площини, кути
– координати одиничного вектора, який
проведено із початку координат
перпендикулярно до площини, кути
![]() — кути, які утворює цей вектор відповідно
з координатними осями,
— кути, які утворює цей вектор відповідно
з координатними осями,
![]() — довжина перпендикуляра, проведеного
із початку координат до цієї площини
(рис. 6).
— довжина перпендикуляра, проведеного
із початку координат до цієї площини
(рис. 6).
Для
приведення загального рівняння площини
![]() до нормального вигляду необхідно його
помножити на нормуючий множник:
до нормального вигляду необхідно його
помножити на нормуючий множник:
 (10)
(10)
Знак
нормуючого множника
![]() береться
протилежним до знака вільного члена
береться
протилежним до знака вільного члена
![]() .
.
Відстань від точки до площини
Відстань
від точки
![]() до площини
до площини
![]() є довжиною перпендикуляра, опущеного
із цієї точки на площину. Вона обчислюється
за формулою:
є довжиною перпендикуляра, опущеного
із цієї точки на площину. Вона обчислюється
за формулою:
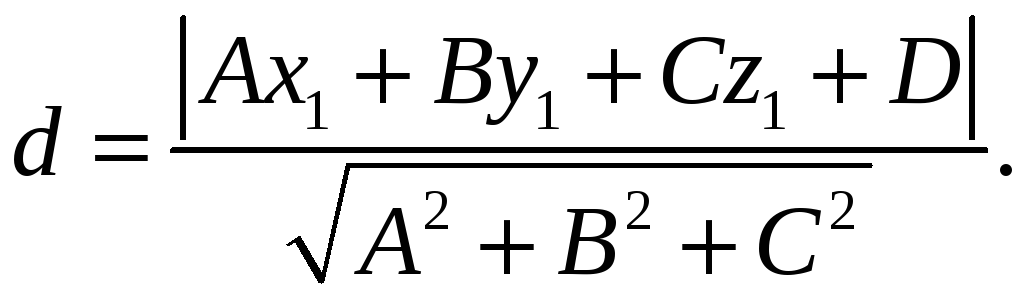 (11)
(11)
Правило.
Щоб
визначити відстань від точки
![]() до площини
до площини
![]() ,
треба дане рівняння площини привести
до нормального вигляду, потім у ліву
частину одержаного рівняння підставити
замість змінних координат координати
даної точки. Абсолютна величина одержаного
числа і буде шуканою відстанню.
,
треба дане рівняння площини привести
до нормального вигляду, потім у ліву
частину одержаного рівняння підставити
замість змінних координат координати
даної точки. Абсолютна величина одержаного
числа і буде шуканою відстанню.
Взаємне розташування двох площин в просторі
Задано
дві площини
![]() рівняннями:
рівняннями:
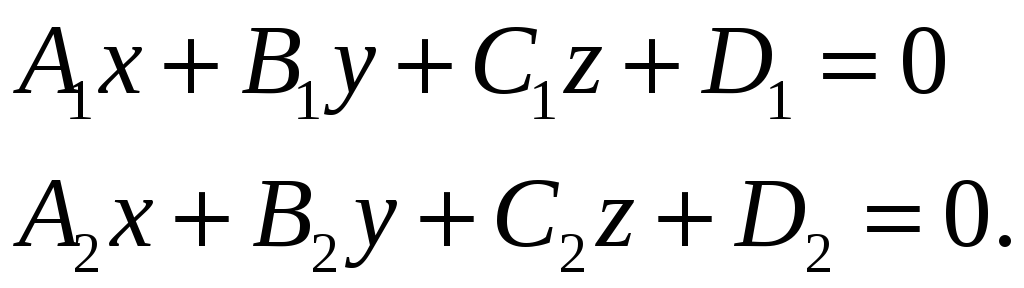 (12)
(12)
Складемо матриці виду:
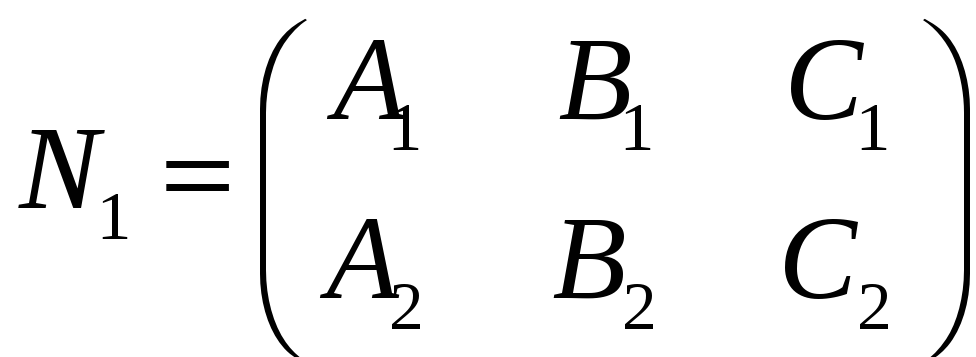 та
та
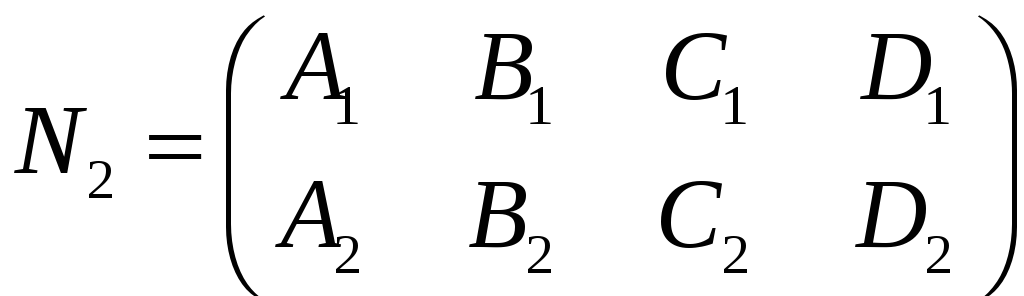 .
.
Н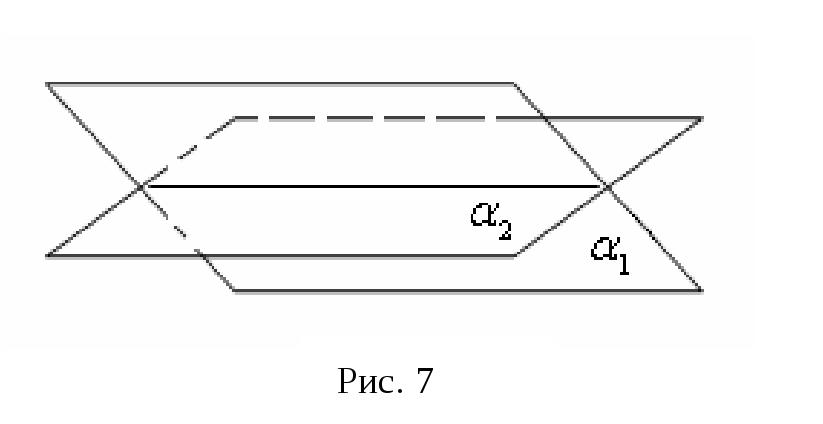 ехай
ехай
![]() і
і
![]() – ранги відповідно матриць
– ранги відповідно матриць
![]() та
та
![]() (причому
(причому
![]() ).
).
Можливий один із наступних випадків:
-
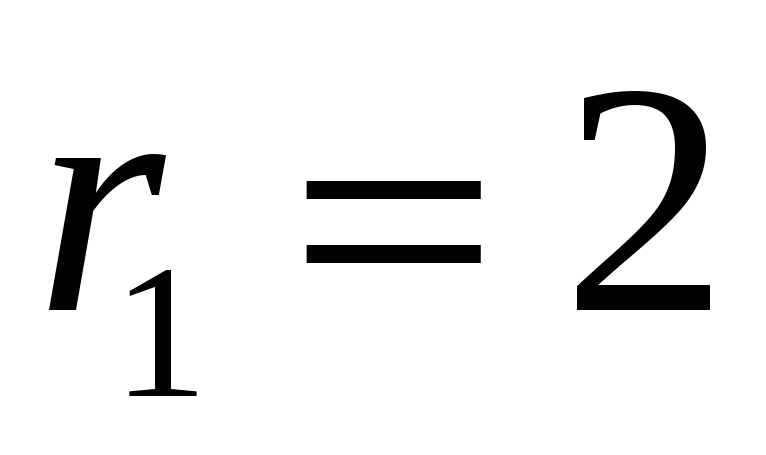 .
В цьому випадку
.
В цьому випадку
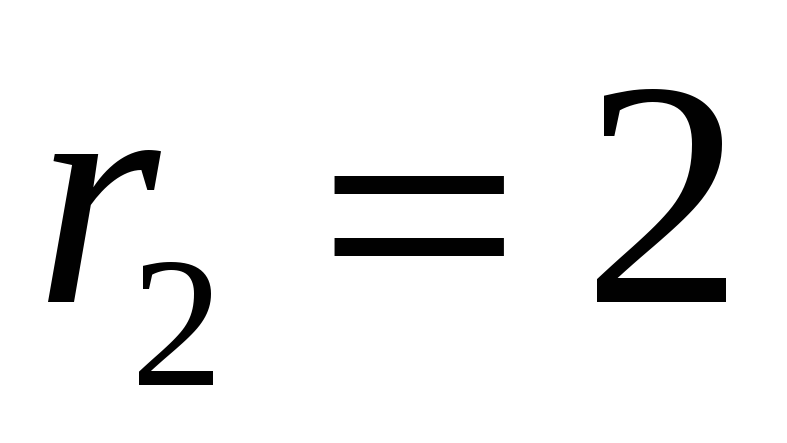 та система рівнянь (12) має нескінченну
множину розв’язків
та система рівнянь (12) має нескінченну
множину розв’язків
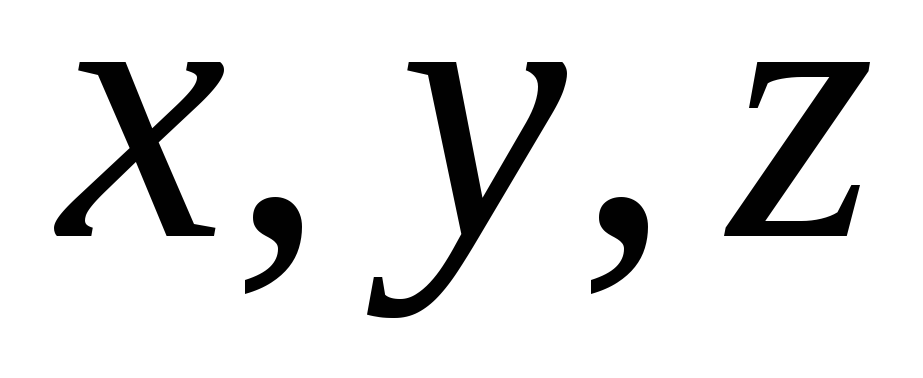 і площини
і площини
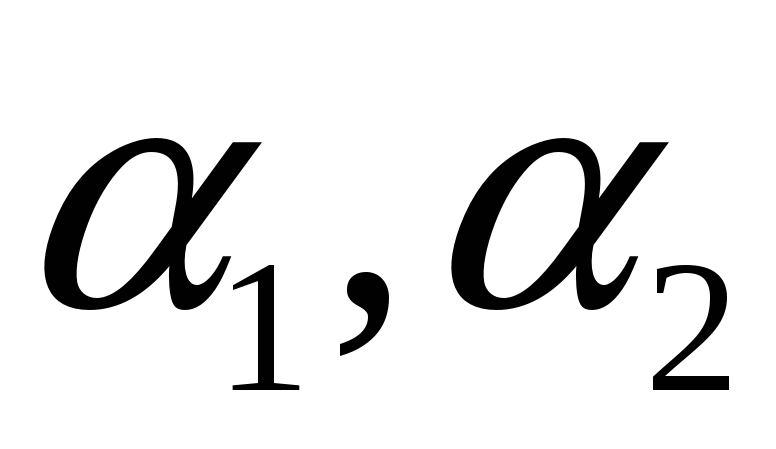 перетинаються по прямій (рис. 7).
перетинаються по прямій (рис. 7). -
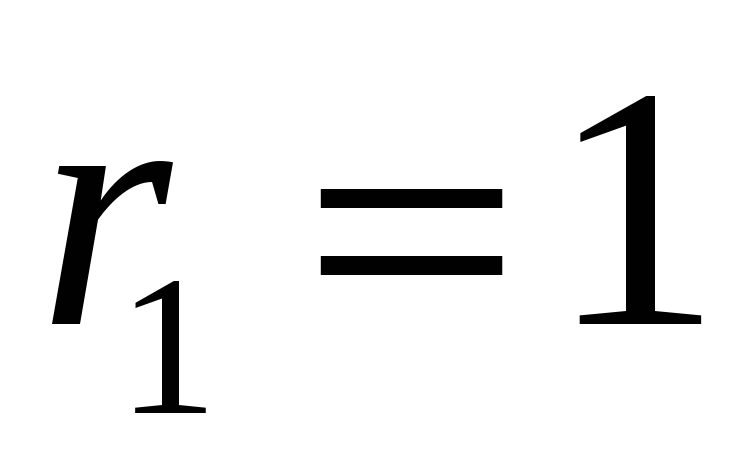
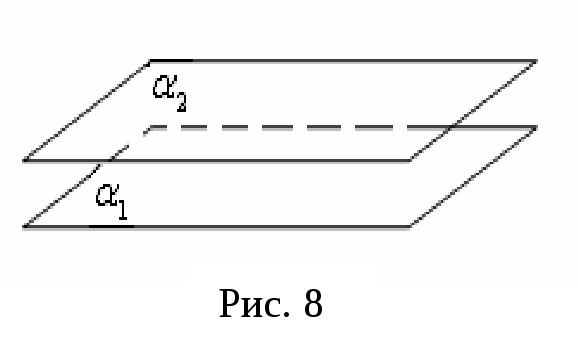 ,
,
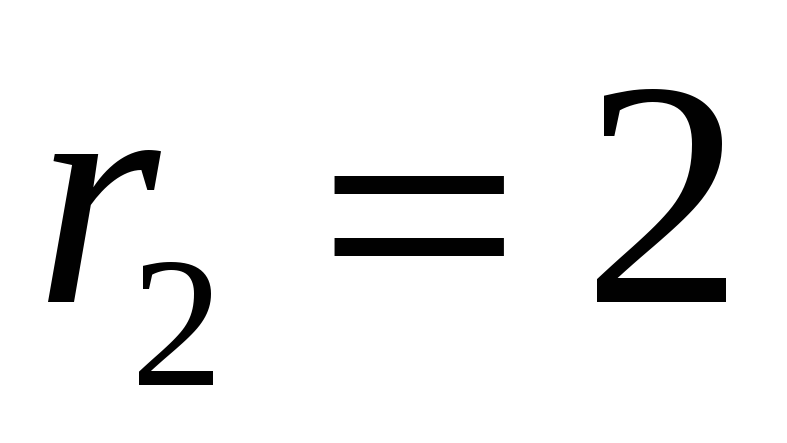 .
В цьому випадку система рівнянь (12) не
має розв’язків і тому площини
.
В цьому випадку система рівнянь (12) не
має розв’язків і тому площини
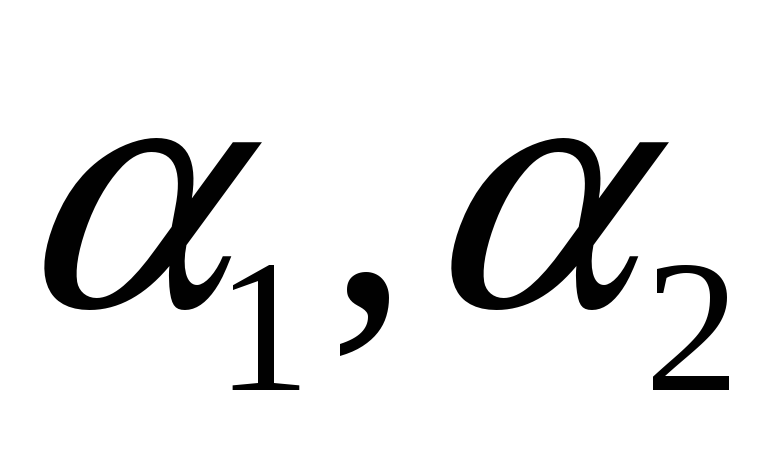 паралельні (рис. 8).
паралельні (рис. 8). -
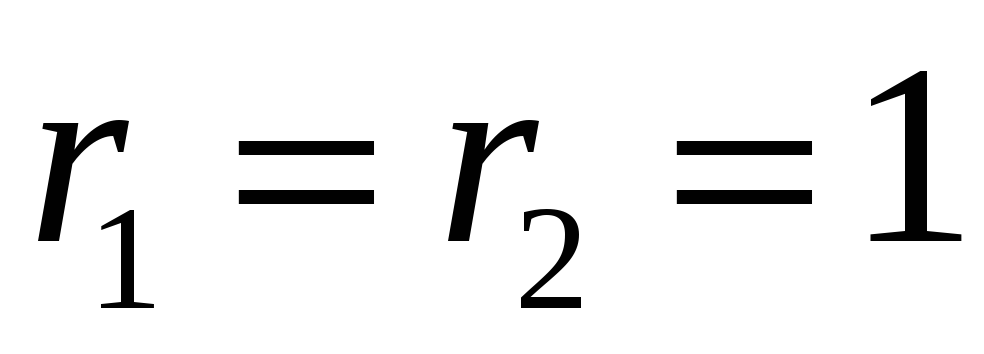 .
За цих умов рівняння (12) рівносильні і,
отже, вони є рівняннями однієї і тієї
ж площини (рис. 9).
.
За цих умов рівняння (12) рівносильні і,
отже, вони є рівняннями однієї і тієї
ж площини (рис. 9).
Взаємне розташування трьох площин в просторі
Три площини в просторі можуть бути розташовані наступним чином:
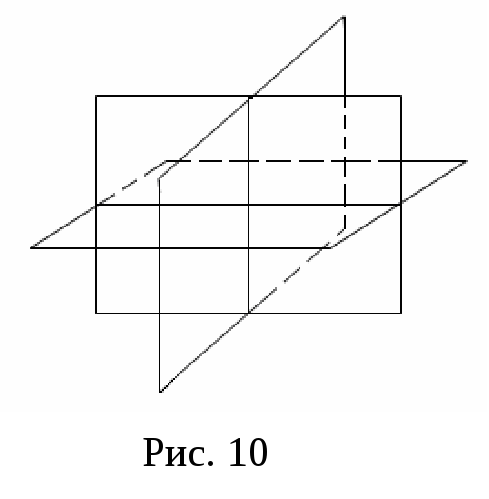
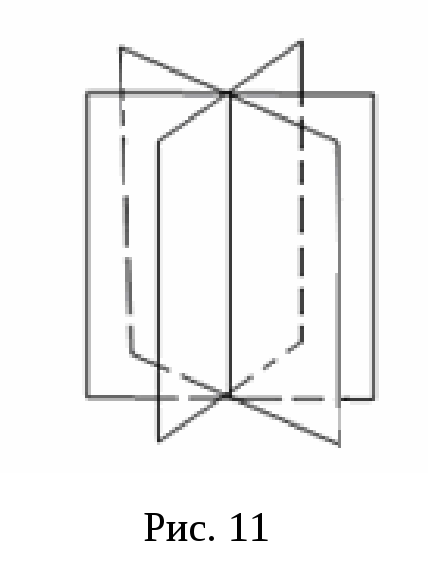
мають одну спільну точку (рис. 10) пучок площин (рис. 11)
попарний перетин по перетин по двох прямих (рис. 13)
т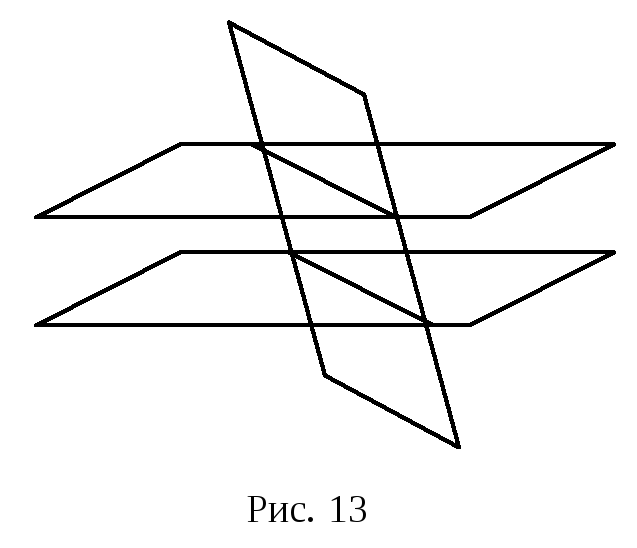 рьох
прямих (рис. 12)
рьох
прямих (рис. 12)

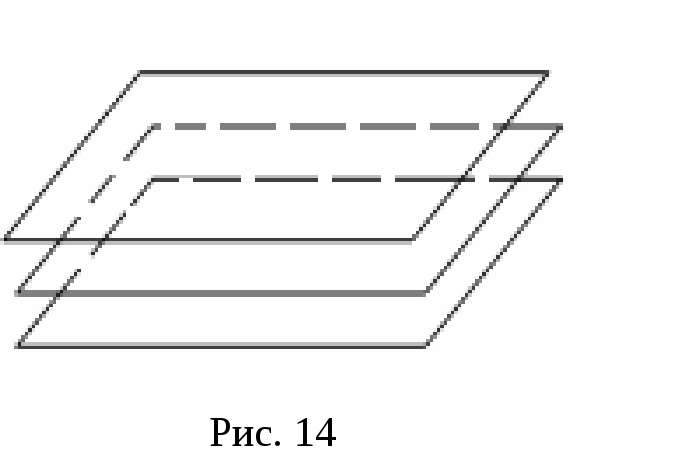
паралельні площини (рис. 14) дві співпадають, третя перетинає (рис.15)
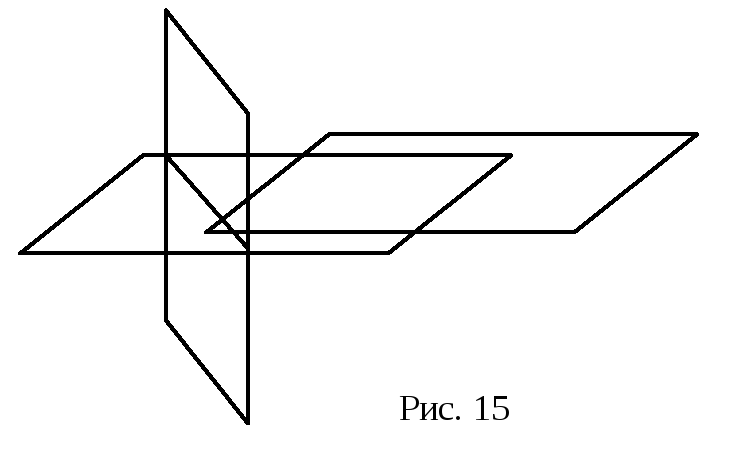
дві співпадають, третя паралельна (рис. 16) співпадають (рис. 17)
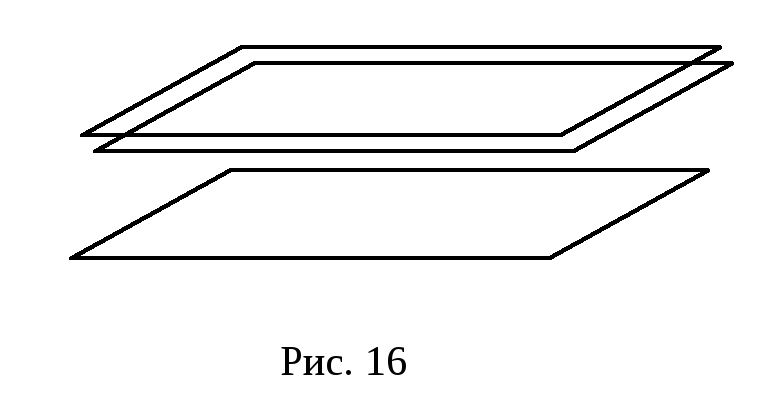
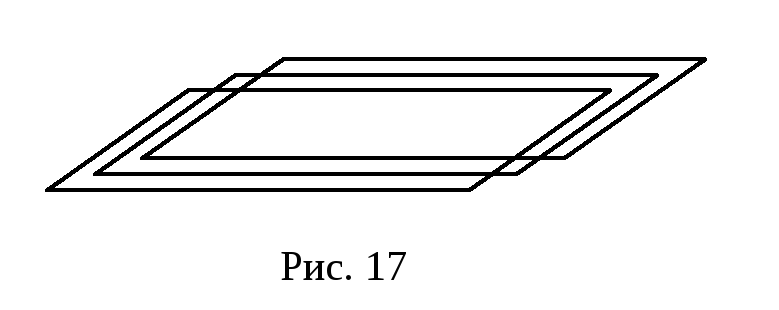
Кут між двома площинами
К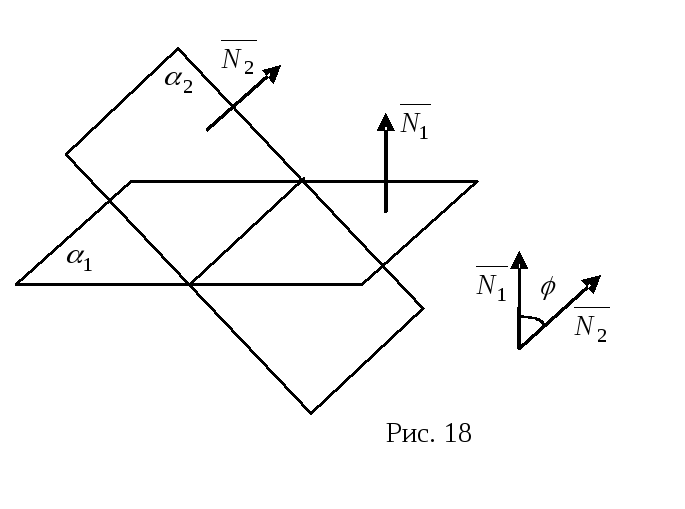 ут
між двома площинами визначається як
кут між нормальними векторами цих
площин. Нехай площини задано загальними
рівняннями
ут
між двома площинами визначається як
кут між нормальними векторами цих
площин. Нехай площини задано загальними
рівняннями
![]() і
і
![]() тоді
нормальним вектором першої площини
буде вектор
тоді
нормальним вектором першої площини
буде вектор
![]() ,
а другої –
,
а другої –
![]() .
Косинус кута між цими векторами, а
значить і між площинами, обчислюється
за формулою:
.
Косинус кута між цими векторами, а
значить і між площинами, обчислюється
за формулою:
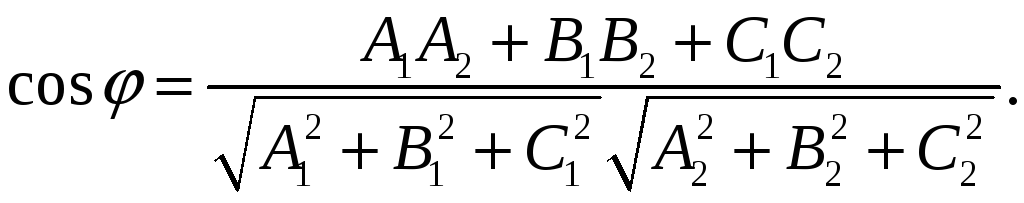 (13)
(13)
Умова
перпендикулярності
двох площин збігається з умовою
перпендикулярності векторів
![]() і
і
![]() та має вигляд:
та має вигляд:
![]() (14)
(14)
Умова
паралельності
двох площин збігається з умовою
колінеарності векторів
![]() і
і
![]() та має вигляд:
та має вигляд:
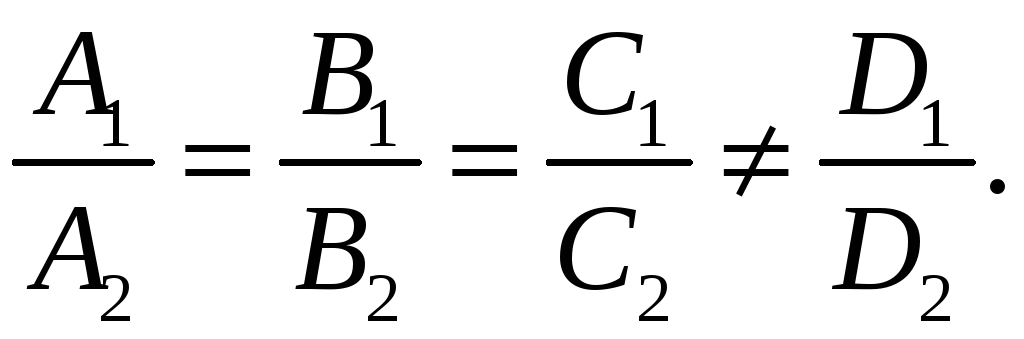 (15)
(15)
Умова співпадіння двох площин має вигляд:
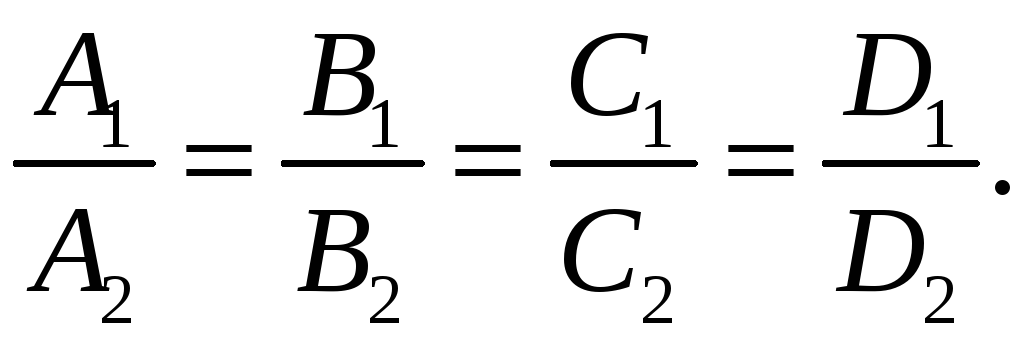
Пучок площин
Пучком площин називається сукупність площин, які проходять через спільну пряму. Ця пряма називається віссю пучка.
Нехай пряма задана двома площинами, що перетинаються:
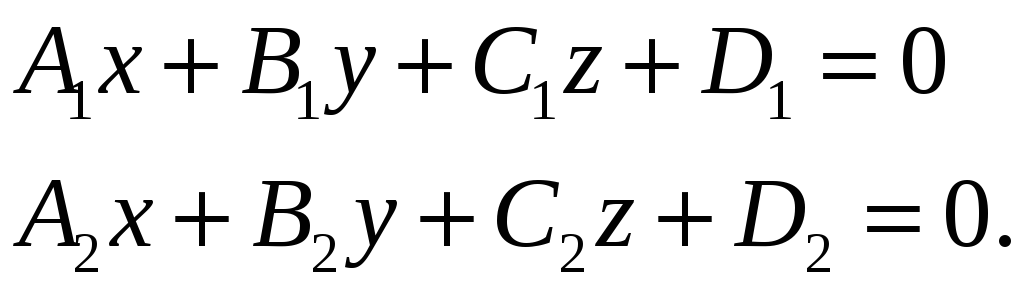 (16)
(16)
Якщо
помножити ці рівності відповідно на
числа
![]() і
і
![]() ,
які не дорівнюють нулю одночасно, а
результати додати, то отримаємо нову
рівність виду:
,
які не дорівнюють нулю одночасно, а
результати додати, то отримаємо нову
рівність виду:
![]() (17)
(17)
Перегрупувавши
члени рівняння (17) відносно
![]() ,
одержимо
,
одержимо
![]() (17’)
(17’)
В рівності
(17’)
коефіцієнти
![]() ,
,
![]() ,
,
![]() одночасно не можуть перетворюватись
на нуль, так як в протилежному випадку
було б
одночасно не можуть перетворюватись
на нуль, так як в протилежному випадку
було б
![]() тобто
тобто
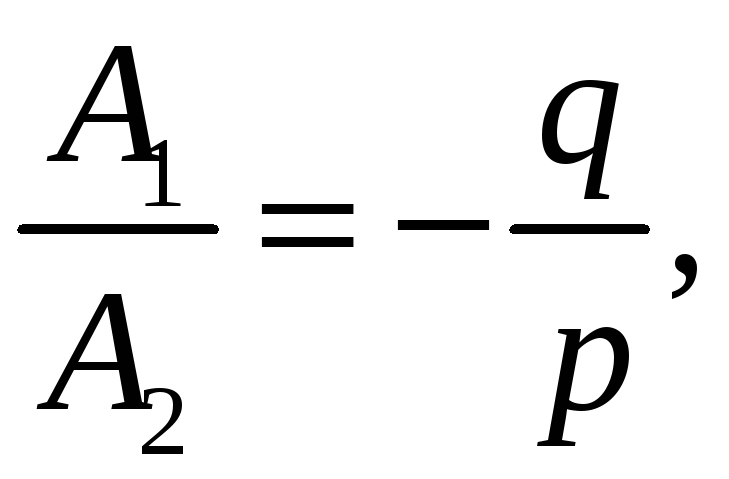
![]() тобто
тобто
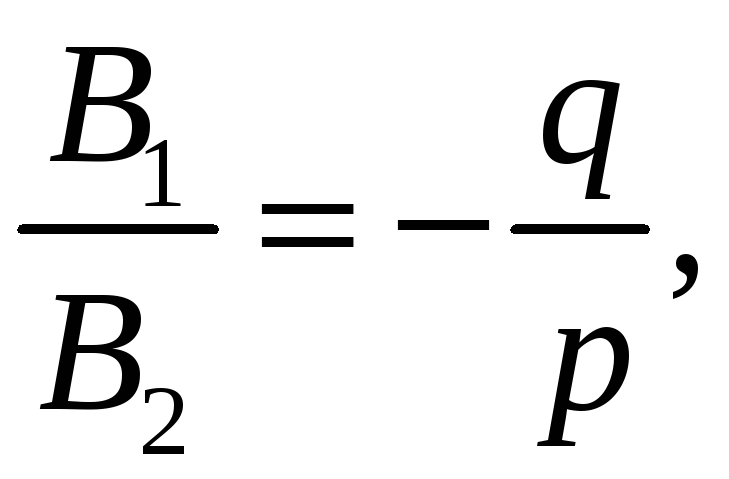
![]() тобто
тобто
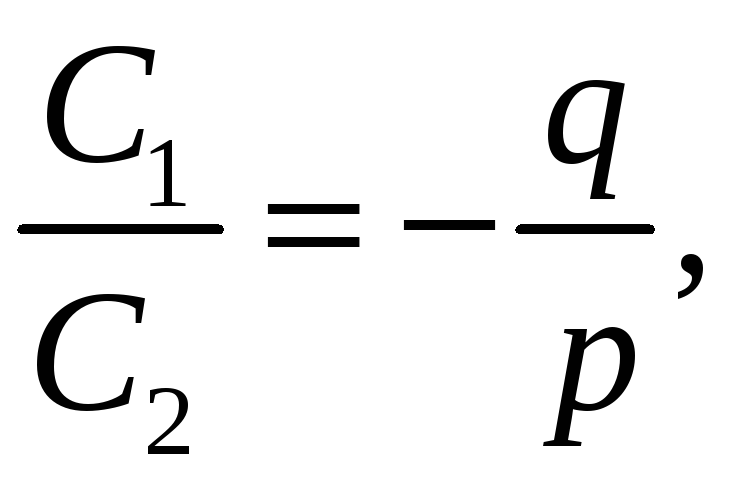
а так
як
![]() і
і
![]() одночасно
не дорівнюють нулю, то
одночасно
не дорівнюють нулю, то
![]() або
або
![]() – певне число і, отже,
– певне число і, отже,
![]()
![]()
![]()
що
суперечить умові про те, що дані площини
перетинаються. Рівняння (17) є рівнянням
деякої нової площини. Координати
будь-якої точки прямої, що одержується
при перетині площин, що задані рівняннями
(16), задовольняють також і рівнянню (17),
так як в цьому рівнянні вирази, що стоять
в дужках, при підстановці в них координат
цих точок перетворяться в нуль. Отже,
площина (17) буде проходити через пряму
перетину площин (16). При різних значеннях
![]() ми будемо отримувати різні площини, що
проходять через одну й ту ж пряму.
ми будемо отримувати різні площини, що
проходять через одну й ту ж пряму.
Розділивши
рівняння (17) на
![]() і позначивши
і позначивши
 ,
одержимо рівняння виду
,
одержимо рівняння виду
![]() (18)
(18)
Рівняння (18) є рівнянням пучка площин, що задається двома площинами цього пучка.
