Розділ 1. Теоретичні відомості до модуля «Площина в просторі» Поняття площини та її рівняння

В курсі елементарної геометрії площина не визначається, так як вона є основним, неозначуваним геометричним об’єктом. Основні властивості площини задаються аксіомами, а інші виводяться з них логічним шляхом. Однак, користуючись поняттям компланарності векторів, можна задати геометричне місце всіх точок простору, що належать площині. Дійсно, якщо М₀ — довільна точка площини , а і — неколінеарні вектори, паралельні цій площині, то точка М належить площині тоді і тільки тоді, коли вектори , і компланарні. Іншими словами, якщо — множина всіх точок, що належать площині , то –– геометричне місце точок М простору, що задовольняють умові: вектори , і компланарні. Ця властивість може бути використана для складання рівняння геометричного місця точок, тобто рівняння площини.

Способи задання площини

1. Площина задається точкою і направляючим підпростором

Вектори, які лежать в одній площині, називаються направляючим двовимірним векторним підпростором трьохвимірного векторного простору.

Н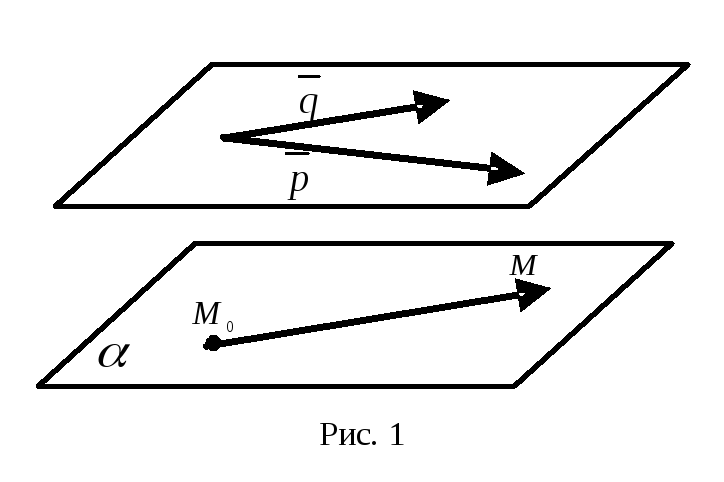ехай – довільна площина, – точка, що належить площині , а вектори і визначають направляючий підпростір даної площини (рис. 1). Візьмемо в площині довільну точку . Оскільки вектори , і компланарні, то виконується умова:

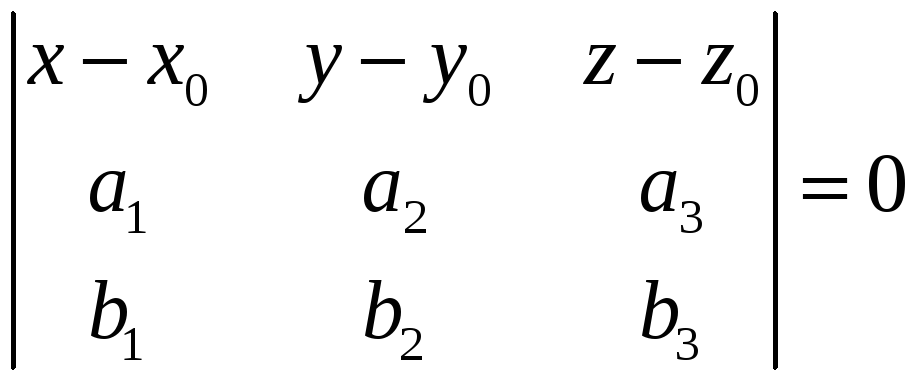(1)

Рівняння (1) є рівнянням площини, що задається точкою і направляючим підпростором.

2. Рівняння площини, що проходить через три точки, які не лежать на одній прямій

Нехай маємо три точки , , , які не лежать на одній прямій (рис. 2).

Розглянемо вектори , . Ці вектори не колінеарні, а тому довільна точка лежить на одній площині з точками , , тоді й тільки тоді, коли вектори ; ; будуть компланарними. Якщо вектори компланарні, то їх мішаний добуток дорівнює нулю:

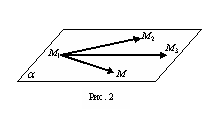
Запишемо цю умову у вигляді:

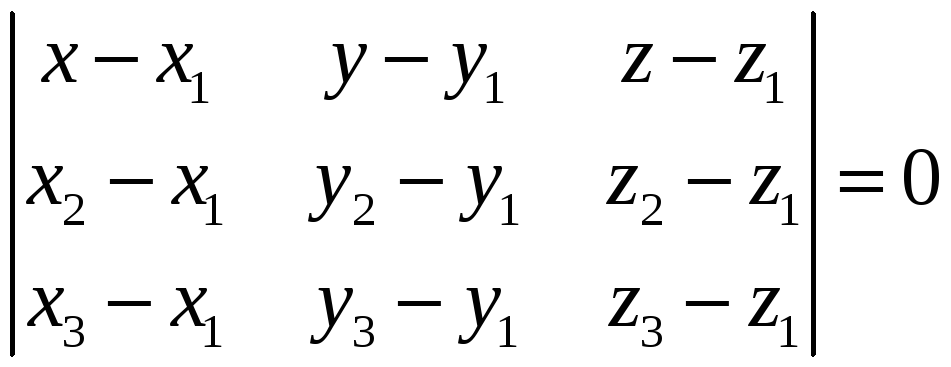(2)

Рівняння (2) називається рівнянням площини, що проходить через три дані точки.

3. Рівняння площини у відрізках

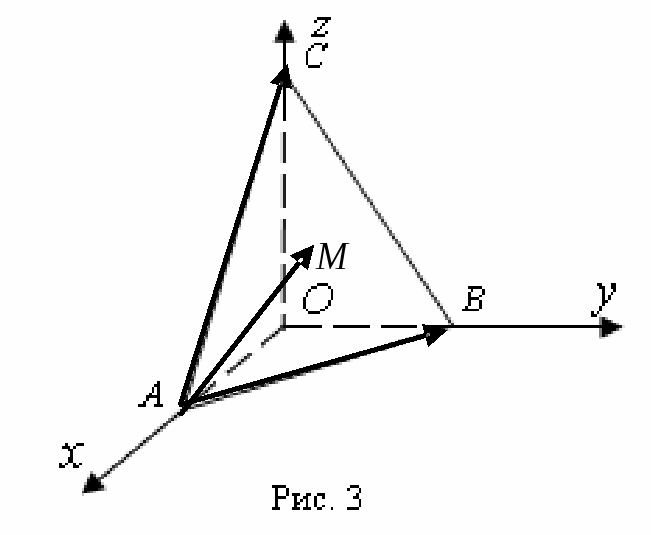
Нехай площина відтинає на осях координат відрізки Тоді , , – точки перетину площини з осями координат (рис. 3). Якщо – довільна точка даної площини, то виконується умова компланарності векторів , , :

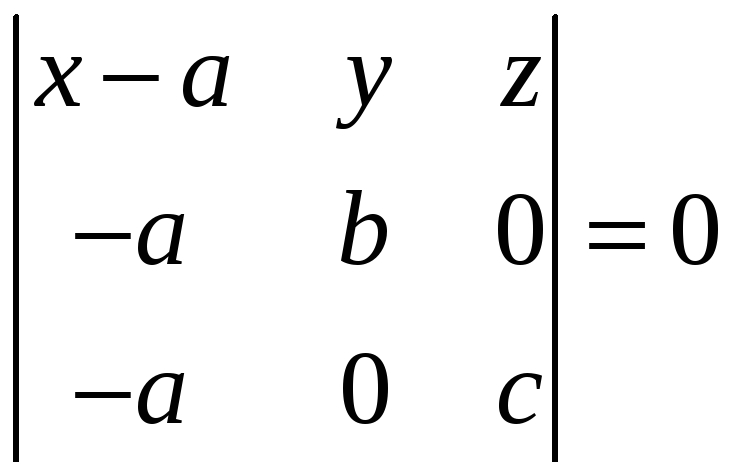
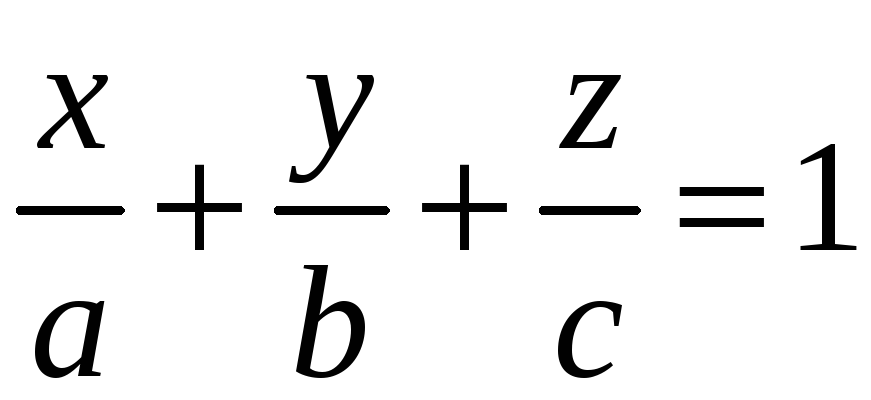(3)

Рівняння (3) називається рівнянням площини у відрізках.

4. Параметричні рівняння площини

Нехай площина задана точкою і направляючими векторами та . Оскільки вектори і не колінеарні, то вектор єдиним чином можна розкласти по векторах і , тобто для будь-якої точки площини існують числа та такі, що

(4)

Запишемо рівність (4) в координатній формі:

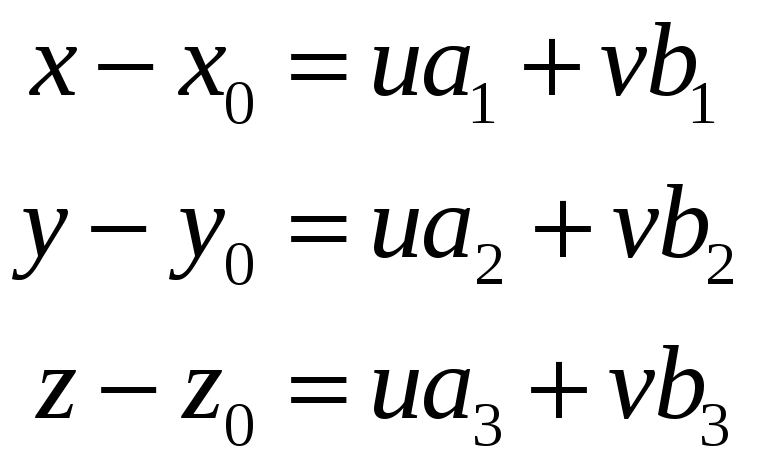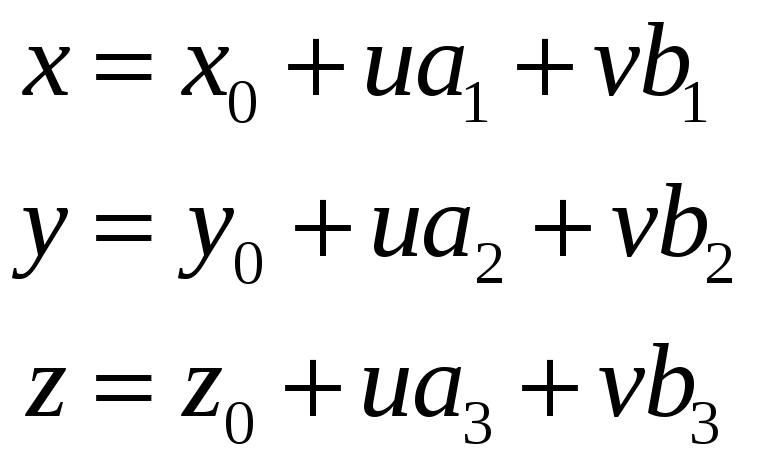або (5)

Рівняння (5) називаються параметричними рівняннями площини.

5. Загальне рівняння площини

Н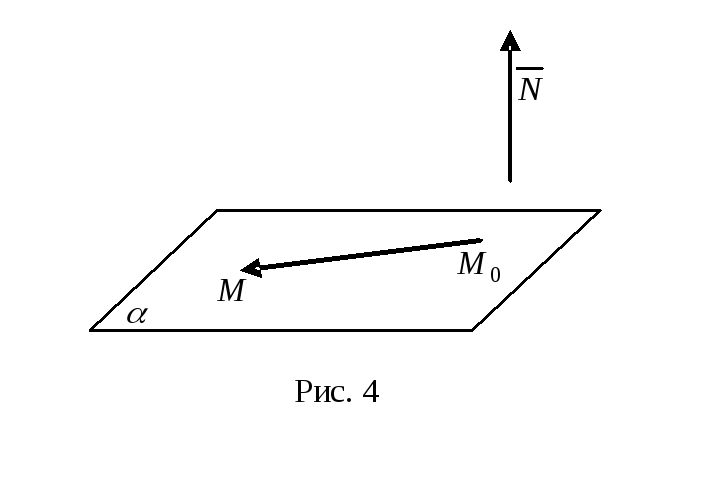ехай площина проходить через точку перпендикулярно до вектора (рис. 4).

Цими умовами визначається єдина площина у просторі. Вектор називається нормальним вектором площини . Візьмемо в площині довільну точку . Тоді вектор буде перпендикулярним до вектора . Значить, скалярний добуток цих векторів дорівнює нулю, тобто .

Одержане рівняння запишемо в координатній формі:

Рівняння площини, записане у вигляді

(6)

(де ), називається загальним рівнянням площини.