- •Введение
- •Информация и сигнал. Общая схема передачи информации
- •1.2. Основные этапы развития радиоэлектроники
- •Сигналы
- •2.1. Классификация сигналов
- •Формы представления детерминированных сигналов
- •2.2. Спектры периодических сигналов
- •Распределение мощности в спектре периодического сигнала
- •Спектры простейших периодических сигналов
- •2.3. Спектры непериодических сигналов
- •Свойства преобразования Фурье
- •Распределение энергии в спектре непериодического сигнала
- •Свойства d-функции
- •2.4. Корреляционный анализ детерминированных сигналов
- •2.5. Радиосигналы - модулированные колебания
- •Спектр амплитудно-модулированного сигнала
- •Спектр радиосигнала при угловой модуляции
- •Балансная и однополосная амплитудные модуляции
- •Импульсно-модулированные сигналы
- •Спектр амплитудно-импульсного модулированного сигнала
- •Внутриимпульсная частотная модуляция
- •2.6. Случайные сигналы Случайные величины
- •Плотность вероятности функции от случайной величины
- •Многомерная плотность вероятности
- •Случайный процесс
- •Спектральный анализ случайных сигналов
- •Примеры случайных процессов
- •1. Постоянное напряжение случайного уровня Ак
- •2. Гармоническое колебание со случайной фазой
- •3. Белый шум
- •2.7. Дискретизация непрерывных сигналов
- •Дискретизация по критерию наибольшего отклонения. Адаптивная дискретизация
- •2.8. Информация и сигнал. Информационная емкость сигналов Количественная оценка информации
- •Информационная емкость дискретного и непрерывного сигналов
- •Непрерывный сигнал
- •Вопросы для самопроверки к главе II.
- •3. Радиотехнические цепи
- •3.1. Квазистационарность тока. Законы Кирхгофа.
- •Принцип суперпозиции для линейной цепи
- •Законы Кирхгофа
- •I закон Кирхгофа
- •II Закон Кирхгофа
- •3.2. Символическая форма для синусоидальных токов, действующие значения, мгновенная, полная, активная и реактивная мощности
- •3.3. Двухполюсники. Комплексное сопротивление двухполюсника
- •Последовательное соединение двухполюсников
- •Параллельное соединение двухполюсников
- •3.4. Методы расчета сложных цепей а) Общий метод
- •Б) Метод контурных токов
- •В) Метод узловых напряжений.
- •3.5. Преобразование Лапласа
- •3.6. Расчет линейных цепей при несинусоидальных эдс и переходных процессах
- •Включение цепи r, l, c под постоянное напряжение
- •Размыкание ключом части сложной цепи
- •3.7. Четырехполюсники
- •Соединения четырехполюсников. Матричная запись уравнений
- •Каскадное соединение
- •Параллельное соединение
- •3.8. Передаточная функция и импульсная характеристика цепи
- •3.9. Передаточная функция соединений четырехполюсников. Обратная связь
- •3.10. Примеры расчета передаточных функций и импульсных
- •Скомпенсированный делитель напряжения
- •Интегрирующая цепь
- •Дифференцирующая цепь
- •Параллельный колебательный контур как четырехполюсник
- •Мост Вина
- •Тройная фазосдвигающая rc-цепь
- •Двойной т-образный мост
- •Система идентичных индуктивно-связанных контуров
- •Резистивный (апериодический) каскад усиления
- •4. Методы анализа прохождения сигналов через цепи
- •4.1. Спектральный метод
- •Условия отсутствия искажений
- •4.2. Метод интеграла наложения Дюамеля
- •4.3. Корреляция сигнала на входе и выходе четырехполюсника
- •Рассмотрим два крайних случая
- •4.4. Анализ прохождения прямоугольного импульса через интегрирующую цепь
- •4.8. Прохождение амплитудно-модулированного сигнала через колебательный контур
- •4.9. Прохождение частотно-модулированного сигнала через колебательный контур
- •4.10. Импульсный трансформатор
- •5.2. Аппроксимация нелинейных характеристик
- •Аппроксимация степенным полиномом
- •Кусочно-линейная аппроксимация
- •Аппроксимация показательной функцией
- •5.3. Воздействие гармонического сигнала на нелинейные элементы. Степенная аппроксимация.
- •Кусочно-линейная аппроксимация
- •Показательная аппроксимация
- •5.4. Воздействие суммы двух гармонических колебаний на нелинейный элемент со степенной характеристикой
- •5.5. Нелинейное резонансное усиление
- •5.6. Умножение частоты
- •5.7. Амплитудная модуляция
- •5.8. Амплитудное детектирование
- •5.9. Преобразование частоты сигнала
- •5.10. Синхронное детектирование
- •6. Линейно-параметрические цепи
- •6.1. Особенности линейно-параметрических цепей
- •6.2. Схема замещения емкости, изменяющейся по гармоническому закону
- •6.3. Одноконтурный параметрический усилитель
- •6.4. Параметрический генератор-параметрон
- •7. Неквазистационарные токи. Цепи с распределенными параметрами
- •7.1. Уравнение телеграфистов. Синусоидальный сигнал
- •7.2. Частный случай пренебрежения затуханием (короткие линии)
- •7.3. Общий случай временной зависимости входного сигнала
- •7.4. Подключение заряженной линии к активному сопротивлению
- •7.5. Волноводы
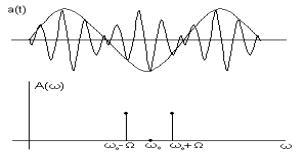
Балансная и однополосная амплитудные модуляции
В амплитудно-модулированном (АМ) сигнале:
![]()
значительная
доля мощности сосредоточена в несущем
колебании![]() Для
более эффективного использования
мощности передатчика можно формировать
АМ-сигналы с подавленным несущим
колебанием, реализуя так называемую
балансную амплитудную модуляцию.
Для
более эффективного использования
мощности передатчика можно формировать
АМ-сигналы с подавленным несущим
колебанием, реализуя так называемую
балансную амплитудную модуляцию.
|
|
Однотональный АМ-сигнал с балансной модуляцией имеет вид:
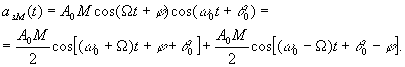
Такой
сигнал с физической точки зрения является
биением двух гармонических сигналов с
одинаковыми амплитудами ![]()
![]() и
частотами
и
частотами ![]() и
и ![]() .
При переходе огибающей биений через
нуль фаза высокочастотного заполнения
скачком изменяется на 180о,
поскольку функция
.
При переходе огибающей биений через
нуль фаза высокочастотного заполнения
скачком изменяется на 180о,
поскольку функция ![]() имеет
разные знаки справа и слева от нуля.
Осуществление балансной модуляции, как
и обратного процесса демодуляции
(детектирования), технически более
сложно, чем при обычной амплитудной
модуляции.
имеет
разные знаки справа и слева от нуля.
Осуществление балансной модуляции, как
и обратного процесса демодуляции
(детектирования), технически более
сложно, чем при обычной амплитудной
модуляции.
Другим усовершенствованием обычной амплитудной модуляции является удаление всех гармоник справа или слева от несущей частоты. При этом информация не теряется, так как содержится в оставшихся гармониках с другой стороны от несущей. Такая модуляция называетсяоднополосной и позволяет в два раза сократить полосу занимаемых частот радиоканала, при этом существенно усложняется процесс демодуляции с полным восстановлением модулирующего сигнала. Возможно устранение в однополосной модуляции и несущего колебания с частотой w0.
|
|
Обобщенное представление радиосигнала в виде высокочастотного узкополосного колебания. Аналитический сигнал
Используются
радиосигналы, получаемые в результате
одновременной модуляции амплитуды и
угла ![]() .
При этом может возникнуть неоднозначность
в выборе функций A(t), y(t) (можно A(t)представить
в виде cos, а y(t) - в
виде arccos и поменять местами). Однако
если сигнал является узкополосным
(ширина спектра модулирующих функций
много меньше центральной частоты w0),
то неопределенностейA(t) и y(t) можно
избежать с помощью следующих соотношений:
.
При этом может возникнуть неоднозначность
в выборе функций A(t), y(t) (можно A(t)представить
в виде cos, а y(t) - в
виде arccos и поменять местами). Однако
если сигнал является узкополосным
(ширина спектра модулирующих функций
много меньше центральной частоты w0),
то неопределенностейA(t) и y(t) можно
избежать с помощью следующих соотношений:
![]() ;
(1)
;
(1)
![]() (2)
(2)
где a1(t) - новая функция, связанная с исходной преобразованием Гильберта;
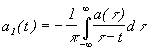 ;
(3)
;
(3)
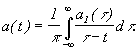 (4)
(4)
Мгновенная частота узкополосного сигнала равна:
![]() .
.
Выделив
в ![]() постоянную
часть
постоянную
часть ![]() ,
можно написать
,
можно написать![]() ,
где
,
где ![]() не
содержит слагаемого, линейно зависящего
от времени.
не
содержит слагаемого, линейно зависящего
от времени.
Из
(1) следует, что в точках, где a1(t)
= 0 имеем ![]()
![]() т.
к.
т.
к. ![]() .
.
Следовательно, в этих точках кривые a(t) и A(t) имеют общие касательные. Кроме того, преобразование Гильберта обеспечивает в точках, где a1(t)=0, значения a(t), близкие к максимальным (амплитудным). Таким образом, функция A(t) касается функции a(t) в ее амплитудных значениях и ее можно считать простейшей огибающей, если она изменяется медленно по сравнению с быстро осциллирующей функцией a(t), т. е. выполнено условие узкополосного сигнала.
Аналитическим представлением сигнала a(t) является комплексный сигнал
![]() где
где![]() - комплексная
огибающая узкополосного сигнала.
- комплексная
огибающая узкополосного сигнала.
Для
спектральных плотностей
функций a(t) и a1(t) имеют
место соотношения ![]() w
> 0,
w
> 0,
![]()
![]() w < 0,
w < 0, ![]()
Спектры аналитического сигнала имеют только положительные частоты.
Корреляционная функция аналитического сигнала
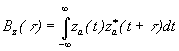 связана
с корреляционной функцией узкополосного
сигнала
связана
с корреляционной функцией узкополосного
сигнала  соотношениями
соотношениями
![]()
![]()
Пример. a(t) = cosw0t.
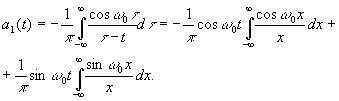
Здесь использована замена t - t = x;
![]()
Известно,
что 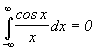 и
и 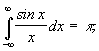 тогда
тогда
![]()
![]() при
при ![]()
![]()