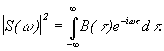- •Введение
- •Информация и сигнал. Общая схема передачи информации
- •1.2. Основные этапы развития радиоэлектроники
- •Сигналы
- •2.1. Классификация сигналов
- •Формы представления детерминированных сигналов
- •2.2. Спектры периодических сигналов
- •Распределение мощности в спектре периодического сигнала
- •Спектры простейших периодических сигналов
- •2.3. Спектры непериодических сигналов
- •Свойства преобразования Фурье
- •Распределение энергии в спектре непериодического сигнала
- •Свойства d-функции
- •2.4. Корреляционный анализ детерминированных сигналов
- •2.5. Радиосигналы - модулированные колебания
- •Спектр амплитудно-модулированного сигнала
- •Спектр радиосигнала при угловой модуляции
- •Балансная и однополосная амплитудные модуляции
- •Импульсно-модулированные сигналы
- •Спектр амплитудно-импульсного модулированного сигнала
- •Внутриимпульсная частотная модуляция
- •2.6. Случайные сигналы Случайные величины
- •Плотность вероятности функции от случайной величины
- •Многомерная плотность вероятности
- •Случайный процесс
- •Спектральный анализ случайных сигналов
- •Примеры случайных процессов
- •1. Постоянное напряжение случайного уровня Ак
- •2. Гармоническое колебание со случайной фазой
- •3. Белый шум
- •2.7. Дискретизация непрерывных сигналов
- •Дискретизация по критерию наибольшего отклонения. Адаптивная дискретизация
- •2.8. Информация и сигнал. Информационная емкость сигналов Количественная оценка информации
- •Информационная емкость дискретного и непрерывного сигналов
- •Непрерывный сигнал
- •Вопросы для самопроверки к главе II.
- •3. Радиотехнические цепи
- •3.1. Квазистационарность тока. Законы Кирхгофа.
- •Принцип суперпозиции для линейной цепи
- •Законы Кирхгофа
- •I закон Кирхгофа
- •II Закон Кирхгофа
- •3.2. Символическая форма для синусоидальных токов, действующие значения, мгновенная, полная, активная и реактивная мощности
- •3.3. Двухполюсники. Комплексное сопротивление двухполюсника
- •Последовательное соединение двухполюсников
- •Параллельное соединение двухполюсников
- •3.4. Методы расчета сложных цепей а) Общий метод
- •Б) Метод контурных токов
- •В) Метод узловых напряжений.
- •3.5. Преобразование Лапласа
- •3.6. Расчет линейных цепей при несинусоидальных эдс и переходных процессах
- •Включение цепи r, l, c под постоянное напряжение
- •Размыкание ключом части сложной цепи
- •3.7. Четырехполюсники
- •Соединения четырехполюсников. Матричная запись уравнений
- •Каскадное соединение
- •Параллельное соединение
- •3.8. Передаточная функция и импульсная характеристика цепи
- •3.9. Передаточная функция соединений четырехполюсников. Обратная связь
- •3.10. Примеры расчета передаточных функций и импульсных
- •Скомпенсированный делитель напряжения
- •Интегрирующая цепь
- •Дифференцирующая цепь
- •Параллельный колебательный контур как четырехполюсник
- •Мост Вина
- •Тройная фазосдвигающая rc-цепь
- •Двойной т-образный мост
- •Система идентичных индуктивно-связанных контуров
- •Резистивный (апериодический) каскад усиления
- •4. Методы анализа прохождения сигналов через цепи
- •4.1. Спектральный метод
- •Условия отсутствия искажений
- •4.2. Метод интеграла наложения Дюамеля
- •4.3. Корреляция сигнала на входе и выходе четырехполюсника
- •Рассмотрим два крайних случая
- •4.4. Анализ прохождения прямоугольного импульса через интегрирующую цепь
- •4.8. Прохождение амплитудно-модулированного сигнала через колебательный контур
- •4.9. Прохождение частотно-модулированного сигнала через колебательный контур
- •4.10. Импульсный трансформатор
- •5.2. Аппроксимация нелинейных характеристик
- •Аппроксимация степенным полиномом
- •Кусочно-линейная аппроксимация
- •Аппроксимация показательной функцией
- •5.3. Воздействие гармонического сигнала на нелинейные элементы. Степенная аппроксимация.
- •Кусочно-линейная аппроксимация
- •Показательная аппроксимация
- •5.4. Воздействие суммы двух гармонических колебаний на нелинейный элемент со степенной характеристикой
- •5.5. Нелинейное резонансное усиление
- •5.6. Умножение частоты
- •5.7. Амплитудная модуляция
- •5.8. Амплитудное детектирование
- •5.9. Преобразование частоты сигнала
- •5.10. Синхронное детектирование
- •6. Линейно-параметрические цепи
- •6.1. Особенности линейно-параметрических цепей
- •6.2. Схема замещения емкости, изменяющейся по гармоническому закону
- •6.3. Одноконтурный параметрический усилитель
- •6.4. Параметрический генератор-параметрон
- •7. Неквазистационарные токи. Цепи с распределенными параметрами
- •7.1. Уравнение телеграфистов. Синусоидальный сигнал
- •7.2. Частный случай пренебрежения затуханием (короткие линии)
- •7.3. Общий случай временной зависимости входного сигнала
- •7.4. Подключение заряженной линии к активному сопротивлению
- •7.5. Волноводы
Распределение энергии в спектре непериодического сигнала
Найдем спектр квадрата функции s(t).
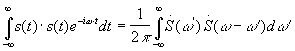 - используем
свойства преобразования Фурье для
произведения двух функций.
- используем
свойства преобразования Фурье для
произведения двух функций.
В
частном случае ( ![]() )
будем иметь:
)
будем иметь:
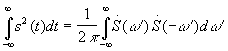 .
Переходя от
.
Переходя от ![]() к
к ![]() и
т. к.
и
т. к.![]() ,
комплексное сопряженние
,
комплексное сопряженние ![]() .
.
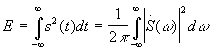 - равенство
Парсеваля.
- равенство
Парсеваля.
![]() - спектральная
плотность энергии (энергия, приходящаяся
на единицу полосы частот). Е - полная
энергия сигнала.
- спектральная
плотность энергии (энергия, приходящаяся
на единицу полосы частот). Е - полная
энергия сигнала.
Для энергии, приходящейся на конечную полосу частот, получим:
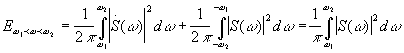 - при
симметричной
- при
симметричной ![]()
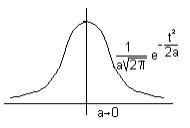
Примеры. Спектр Гауссова (колокольного) импульса
|
|
![]() ,
-¥ < t < ¥, а - условная
половина длительности на уровне 0,606.
,
-¥ < t < ¥, а - условная
половина длительности на уровне 0,606.
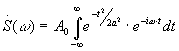 .
.
Произведем преобразование в показателях степени:
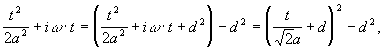
где d - определяется из условия:
![]() откуда
откуда ![]()
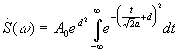 .
.
При d - конечном 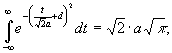 т.
к.
т.
к.  .
.
Тогда 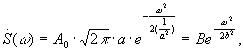 т.
е. спектр Гауссова импульса имеет
Гауссову форму:
т.
е. спектр Гауссова импульса имеет
Гауссову форму: ![]()
![]() .
.
Можно
показать, что Гауссов импульс обладает
наименьшим ![]() при
среднеквадратичном их определении.
при
среднеквадратичном их определении.
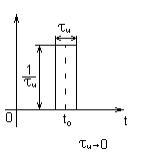
Спектр d-функции
|
|
|
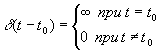 .
.
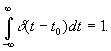
В качестве d-функции может выступать сигнал любой формы с бесконечно малой длительностью и единичной площадью.
Свойства d-функции
1) 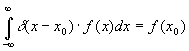 - фильтрующее
свойство.
- фильтрующее
свойство.
2) Четность ![]()
3) Нормировка ![]()
Спектральная плотность
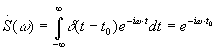 .
.
При t0 =
0, ![]() ,
,
при t0 ¹ 0, ![]() .
.
|
|
![]() - это
спектральное определение d-функции.
- это
спектральное определение d-функции.
Аналогично ![]() - определение d-функции
в частотной области.
- определение d-функции
в частотной области.
Спектральная плотность гармонического колебания
|
|
Одним
из условий применения интегрального
преобразования Фурье функцииs(t) является
ее абсолютная интегрируемость Применениеd-функции позволяет получить спектральную плотность и для неинтегрируемых функций. |
Пусть ![]() Найдем
спектральную плотность, формально не
обращая внимания, что сигнал абсолютно
не интегрируем.
Найдем
спектральную плотность, формально не
обращая внимания, что сигнал абсолютно
не интегрируем.
Произведем
замену ![]() .
.
![]()
Но ![]() тогда
тогда
![]() .
.
Гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность на дискретных частотах ±w0.
В
частности, для постоянного напряжения w0 =
0, ![]()
![]()
2.4. Корреляционный анализ детерминированных сигналов
Корреляционный анализ - это анализ временной зависимости сигналов.
Взаимно-корреляционная функция
Для
оценки степени связи во времени между
двумя различными сигналами ![]() и
и ![]() используется
взаимно-корреляционная функция ВКФ.
используется
взаимно-корреляционная функция ВКФ. 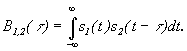
|
|
Найдем
спектральную плотность ВКФ. Для этого
рассмотрим сначала спектральную
плотность произведения двух
функций |
![]()
С
другой стороны, согласно общей формуле
определения спектральной плотности 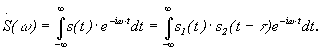
Положим в обеих формулах w = 0, получим:
![]()
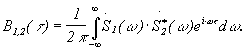
Итак, согласно общему интегральному представлению спектра сигнала спектральная плотность для ВКФ равна произведению спектральной плотности одной функции на сопряженную спектральную плотность другой.
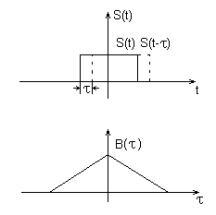
Автокорреляционная функция сигнала (АКФ)
АКФ - это степень связи сигнала s(t) с его копией, сдвинутой на величину t.
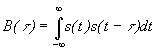 ,
при t =
0
,
при t =
0 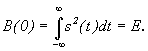
|
|
Максимальное
значение автокорреляционной функции
(при t =
0) равно
энергии сигнала, т. к. сигнал полностью
коррелирован сам с собой. Полагая в
преобразовании Фурье взаимнокорреляционной
функции
|
При t =
0 получим
равенство Парсеваля ![]() .
.
Итак, в частотной области имеется две характеристики сигнала:спектральная плотность и спектральная плотность энергии.
Спектральной
плотности ![]() ,
содержащей полную информацию о сигнале,
соответствует в преобразовании Фурье
сам сигнал s(t).
Спектральной плотности энергии
сигнала
,
содержащей полную информацию о сигнале,
соответствует в преобразовании Фурье
сам сигнал s(t).
Спектральной плотности энергии
сигнала ![]() ,
лишенной фазовой информации, в
преобразовании Фурье соответствует
автокорреляционная функция сигнала
,
лишенной фазовой информации, в
преобразовании Фурье соответствует
автокорреляционная функция сигнала ![]() .
.
Для периодических функций энергия бесконечна, поэтому автокорреляционная функция определяется путем усреднения по периоду:
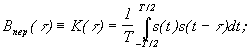
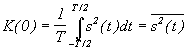 - средняя
мощность сигнала.
- средняя
мощность сигнала.
В более общем случае не обязательно периодического, но с бесконечной полной энергией сигнала принимают:
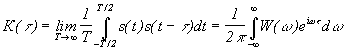 .
.
Фурье
образом такой автокорреляционной
функции будет спектральная плотность
мощности W(w),
что видно из соотношения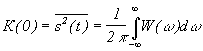 .
Формально
.
Формально ![]()
Однако
практически спектральная плотность
мощности определяется через функцию
автокорреляции 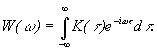
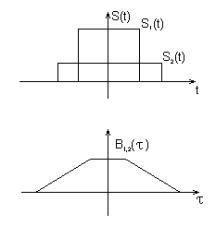
Пример. Автокорреляционная функция прямоугольного импульса
|
|
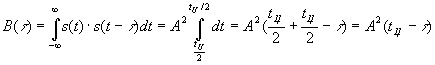 при
при![]()

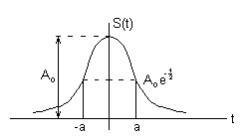
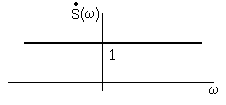
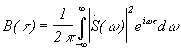 ,
,