6.4. Параметрический генератор-параметрон

     Параметрический генератор можно получить из параметрического усилителя при модуляции нелинейной емкости выше критического значения.

Пусть закон изменения емкости определяется выражением  , где ω0– резонансная частота контура при отсутствии накачки  .

     Сопротивление R включает в себя сопротивление индуктивности и сопротивление нагрузки. Запишем дифференциальное уравнение для тока в контуре:

 , или переходя к заряду:  ,

 , где  .

     При высокой добротности контура Q_экв >> 1 решение будет в виде колебания с частотой ω₀ и медленно меняющейся амплитудой: , при этом ξ = 0, либо ξ = π – два устойчивых решения, отличающихся знаком,  , что легко проверить подстановкой.

     Для нарастания амплитуды должно выполняться условие µ > 0; , что совпадает с определением m_КР.

     Со временем амплитуда колебаний ограничивается заходом амплитуды на нелинейный участок характеристики C(t), расстройкой контура относительно частоты ω₀ и ухудшением условий преобразования энергии накачки.

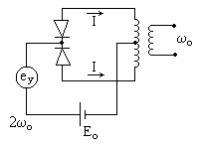
     Параметроны могут применяться в устройствах обработки дискретной информации из-за двузначности фазы генерируемых колебаний ξ = 0 и ξ = π при задании в момент запуска генератора начальной фазы с помощью специального сигнала (плюс или минус). В емкостном параметроне в качестве переменной емкости используются два полупроводниковых диода, а индуктивностью контура служит первичная обмотка трансформатора. Напряжение накачки е_у(t) подается на диоды синфазно. При этом исключается прохождение частоты накачки 2ω₀ на выход. Благодаря симметрии устраняется также прохождение колебания ω₀ из контура в цепь накачки. Положение рабочей точки на характеристике p-nпереходов задается постоянным напряжением смещения E₀.

В индуктивном параметроне контур состоит из постоянной емкости и катушек, насаженных на ферритовые сердечники, магнитная проницаемость которых периодически изменяется током накачки I_Н. Катушки включаются встречно.

7. Неквазистационарные токи. Цепи с распределенными параметрами

7.1. Уравнение телеграфистов. Синусоидальный сигнал

     Главным условием выполнения квазистационарности тока, кроме замкнутости цепи является медленность изменения тока по сравнению со скоростью распространения электромагнитного возмущения по цепи, т. е. длина волны распространяющегося электромагнитного колебания должна быть много больше общей длины цепи. В этом случае токи во всех сечениях неразветвленных участков цепи одинаковы, для анализа цепи можно использовать законы Ома и Кирхгофа и, кроме того, можно считать некоторые распределенные параметры в эквивалентной схеме локально сосредоточенными, например, активные сопротивления, индуктивности даже при их совместном распределении.

.

     Однако часто встречаются длинные цепи передач сигналов (сотни километров) или линии не очень длинные, но служащие для передачи сигналов высокой частоты. В этих цепях мгновенные значения тока в различных точках цепи различны, здесь нельзя применять законы Ома и Кирхгофа, нельзя считать распределенные параметры сосредоточенными в одном месте, кроме того, здесь становится существенной и распределенная емкость отдельных элементов цепи друг к другу. Непосредственное применение уравнений Максвелла представляет сложную задачу и выполнимо лишь в отдельных частных случаях.

В качестве примера рассмотрим коаксиальный кабель, подключенный к источнику синусоидального сигнала

     Вследствие симметрии задачи токи текут вдоль оси z, при пренебрежении сопротивлением проводников  , и остается одна составляющая электрического поля   Магнитное поле имеет одну составляющую 

Уравнения Максвелла                                                 (1)

                                                                              (2)

При заданной симметрии       Тогда

                                                                                       (3)

                                                                          (4)

Беря производные по z и заменяя потом первые производные с помощью соседних уравнений, получим уравнение только для Е и В.   

  с решением:

                                                               (5)

                                                                    (6)

где   Таким образом, получаем прямую и обратную волны, распространяющующиеся по z со скоростью

  Согласно закону полного тока  или   Т. о. волнам электромагнитного поля соответствуют волны электрического тока в проводнике.

     При учете активного сопротивления проводников анализ на основании уравнений Максвелла существенно усложняется, в результате амплитуды бегущих волн будут затухать:      где  - константа, определяемая радиусами и материалом проводников, а также зависящая от частоты из-за скин-эффекта. Фазовая скорость волны с увеличением сопротивления начнет несколько снижаться. При малой толщине скин-слоя  .

В случае более сложной цепи (двухпроводная, некоаксиальная линии) задача на основании уравнения Максвелла точно не решается.

     Поэтому в электротехнике быстрых токов прибегают к упрощению.

Распределенную линию разбивают на участки dz, меньшие длины волны, и для таких участков применяют теорию квазистационарных токов, т.е. вводят сосредоточенные      ,

где   - распределенные параметры на единицу длины, и записывают для такого элемента законы Ома и Кирхгофа:

 .                                             (7)

С другой стороны  ;

 ,                                                                                    (8)

т. к. часть тока ответвляется на емкость  .

                                                                            (9)

 .                                                                                  (10)

Условие применения принятого приближения кроме   - малое расстояние между проводниками  , чтобы не влияла взаимная индуктивность и емкость соседних элементов.

     Дифференцируя (9) по   и подставляя   из (10), получим:

Наоборот, дифференцируя (9) по  , а (10) по dz, получим  Это и есть уравнения телеграфистов.

Рассмотрим синусоидальный сигнал 

           

    

Общее решение линейного уравнения  . Имеем прямую и обратную распространяющие волны.

Положим      

отсюда      

    

 ;

Тогда   т. е. a - коэффициент затухания, k -волновой вектор, фазовая скорость волны   При малых потерях на длине волны  ,

                

     - характеристическое сопротивление линии, 

Пример коаксиального кабеля:

    

    С - скорость света.

      т. е. получаем, как и в точном решении, через уравнения Максвелла.