3.9. Передаточная функция соединений четырехполюсников. Обратная связь
|
|
|
|
|
|
При каскадном соединении, когда сигнал последовательно проходит несколько четырехполюсников, их передаточные функции перемножаются:
.
Это непосредственно следует при замене коэффициентов передачи отношением комплексных амплитуд выходных и входных напряжений каждого четырехполюсника.
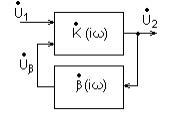
Обратная связь в четырехполюсниках заключается в том, что часть выходного сигнала подается обратно на вход и суммируется с входным сигналом.
|
|
Пусть K(iw)
– передаточная функция основного
четырехполюсника, |
-
передаточная функция четырехполюсника
обратной связи.
; 
.
Отсюда 
.
Итак, общий коэффициент передачи системы с обратной связью есть
.
Если
на заданной частоте w выполняется
неравенство
,
то введение обратной связи уменьшает
модуль общего коэффициента передачи
системы. Такую связь называют отрицательной
обратной связью. При обратном
неравенстве
в
системе реализуется положительная
обратная связь, которая увеличивает
амплитуду выходного сигнала. Положительная
обратная связь ограничена условием 
,
т.к. при переходе этого неравенства в
равенство общий коэффициент передачи
становится бесконечным, а это означает,
что система самовозбуждается, т. е.
появляется выходной сигнал в отсутствие
сигнала на входе.
3.10. Примеры расчета передаточных функций и импульсных
характеристик четырехполюсников
Скомпенсированный делитель напряжения
|
|
|
Мы
имеем последовательное соединение двух
сложных двухполюсников 
,
каждый из которых состоит из двух
параллельно соединенных элементов R и C.
; 
; 
;
; 
,
отсюда
;
при 
и
не зависит от частоты.
Интегрирующая цепь
|
|
|
.
Здесь t = RC – постоянная интегрирующей цепи.
- АЧХ
цепи.
- ФЧХ
цепи.
При 
.
Деление в спектре на “iw”
означает интегрирование сигнала.
Интегрирующая цепь является простейшим
фильтром низких частот с полосой
пропускания 
.
Импульсную
характеристику можно найти через
передаточную функцию с помощью обратного
Фурье-преобразования, но можно ее
определить и непосредственно, подавая
на вход очень короткий прямоугольный
сигнал площадью единица ( 
).
Во время действия сигнала емкость
заряжается током 
,
т. к. напряжение на емкости во время
зарядки 
.
За время импульса емкость получит
заряд 
и
зарядится до напряжения 
,
т. к. 
.
После
прохождения входного импульса емкость
разряжается через источник сигнала и
сопротивление R по
экспоненциальному закону: .
Действительно, 
с
решением 
.
Другим видом интегрирующей цепи
является L-R цепь
|
|
где |
,
.Дифференцирующая цепь
|
|
|
,
где t = RC.
;
.
Действительно,
при подаче на вход сигнала в виде
дельта-функции d(t)
она проходит через емкость на выход,
при этом емкость заряжается до
напряжения 
за
счет поступления положительного
заряда
на
противоположную пластину емкости. После
прохождения входного сигнала емкость
разряжается по экспоненциальному закону
с постоянной RC.
Последовательный колебательный контур
|
|
|
Внутреннее сопротивление источника входит в R.
.
Введем
параметры контура: 
- резонансная
частота,
- характеристическое
сопротивление, 
- добротность,
обычно Q>>1.
Тогда 
при 
,
.
,
т. к. 
.
,
где 
- полоса
пропускания контура.
Импульсную характеристику можно найти, взяв обратное преобразование Фурье от передаточной функции. Переходя к преобразованию Лапласа, будем иметь:
,
где 
- коэффициент
затухания.
Нули
знаменателя 
,
где 
,
т. к.
.
Импульсная
характеристика имеет вид затухающей
синусоиды. За время
,
т. е. амплитуда колебаний уменьшается
в двадцать раз, что близко к разрешающей
способности осциллографа. Таким образом,
видимое число колебаний равно добротности
контура.
|
|
За число периодов n = Q/pамплитуда колебаний уменьшается в е=2,72 раза. |
