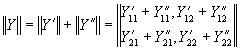- •Введение
- •Информация и сигнал. Общая схема передачи информации
- •1.2. Основные этапы развития радиоэлектроники
- •Сигналы
- •2.1. Классификация сигналов
- •Формы представления детерминированных сигналов
- •2.2. Спектры периодических сигналов
- •Распределение мощности в спектре периодического сигнала
- •Спектры простейших периодических сигналов
- •2.3. Спектры непериодических сигналов
- •Свойства преобразования Фурье
- •Распределение энергии в спектре непериодического сигнала
- •Свойства d-функции
- •2.4. Корреляционный анализ детерминированных сигналов
- •2.5. Радиосигналы - модулированные колебания
- •Спектр амплитудно-модулированного сигнала
- •Спектр радиосигнала при угловой модуляции
- •Балансная и однополосная амплитудные модуляции
- •Импульсно-модулированные сигналы
- •Спектр амплитудно-импульсного модулированного сигнала
- •Внутриимпульсная частотная модуляция
- •2.6. Случайные сигналы Случайные величины
- •Плотность вероятности функции от случайной величины
- •Многомерная плотность вероятности
- •Случайный процесс
- •Спектральный анализ случайных сигналов
- •Примеры случайных процессов
- •1. Постоянное напряжение случайного уровня Ак
- •2. Гармоническое колебание со случайной фазой
- •3. Белый шум
- •2.7. Дискретизация непрерывных сигналов
- •Дискретизация по критерию наибольшего отклонения. Адаптивная дискретизация
- •2.8. Информация и сигнал. Информационная емкость сигналов Количественная оценка информации
- •Информационная емкость дискретного и непрерывного сигналов
- •Непрерывный сигнал
- •Вопросы для самопроверки к главе II.
- •3. Радиотехнические цепи
- •3.1. Квазистационарность тока. Законы Кирхгофа.
- •Принцип суперпозиции для линейной цепи
- •Законы Кирхгофа
- •I закон Кирхгофа
- •II Закон Кирхгофа
- •3.2. Символическая форма для синусоидальных токов, действующие значения, мгновенная, полная, активная и реактивная мощности
- •3.3. Двухполюсники. Комплексное сопротивление двухполюсника
- •Последовательное соединение двухполюсников
- •Параллельное соединение двухполюсников
- •3.4. Методы расчета сложных цепей а) Общий метод
- •Б) Метод контурных токов
- •В) Метод узловых напряжений.
- •3.5. Преобразование Лапласа
- •3.6. Расчет линейных цепей при несинусоидальных эдс и переходных процессах
- •Включение цепи r, l, c под постоянное напряжение
- •Размыкание ключом части сложной цепи
- •3.7. Четырехполюсники
- •Соединения четырехполюсников. Матричная запись уравнений
- •Каскадное соединение
- •Параллельное соединение
- •3.8. Передаточная функция и импульсная характеристика цепи
- •3.9. Передаточная функция соединений четырехполюсников. Обратная связь
- •3.10. Примеры расчета передаточных функций и импульсных
- •Скомпенсированный делитель напряжения
- •Интегрирующая цепь
- •Дифференцирующая цепь
- •Параллельный колебательный контур как четырехполюсник
- •Мост Вина
- •Тройная фазосдвигающая rc-цепь
- •Двойной т-образный мост
- •Система идентичных индуктивно-связанных контуров
- •Резистивный (апериодический) каскад усиления
- •4. Методы анализа прохождения сигналов через цепи
- •4.1. Спектральный метод
- •Условия отсутствия искажений
- •4.2. Метод интеграла наложения Дюамеля
- •4.3. Корреляция сигнала на входе и выходе четырехполюсника
- •Рассмотрим два крайних случая
- •4.4. Анализ прохождения прямоугольного импульса через интегрирующую цепь
- •4.8. Прохождение амплитудно-модулированного сигнала через колебательный контур
- •4.9. Прохождение частотно-модулированного сигнала через колебательный контур
- •4.10. Импульсный трансформатор
- •5.2. Аппроксимация нелинейных характеристик
- •Аппроксимация степенным полиномом
- •Кусочно-линейная аппроксимация
- •Аппроксимация показательной функцией
- •5.3. Воздействие гармонического сигнала на нелинейные элементы. Степенная аппроксимация.
- •Кусочно-линейная аппроксимация
- •Показательная аппроксимация
- •5.4. Воздействие суммы двух гармонических колебаний на нелинейный элемент со степенной характеристикой
- •5.5. Нелинейное резонансное усиление
- •5.6. Умножение частоты
- •5.7. Амплитудная модуляция
- •5.8. Амплитудное детектирование
- •5.9. Преобразование частоты сигнала
- •5.10. Синхронное детектирование
- •6. Линейно-параметрические цепи
- •6.1. Особенности линейно-параметрических цепей
- •6.2. Схема замещения емкости, изменяющейся по гармоническому закону
- •6.3. Одноконтурный параметрический усилитель
- •6.4. Параметрический генератор-параметрон
- •7. Неквазистационарные токи. Цепи с распределенными параметрами
- •7.1. Уравнение телеграфистов. Синусоидальный сигнал
- •7.2. Частный случай пренебрежения затуханием (короткие линии)
- •7.3. Общий случай временной зависимости входного сигнала
- •7.4. Подключение заряженной линии к активному сопротивлению
- •7.5. Волноводы
Соединения четырехполюсников. Матричная запись уравнений
Уравнения четырехполюсника в матричной форме имеют вид:
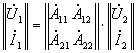 ;
; 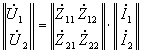 и
др.
и
др.
Матричная запись оказывается целесообразной при анализе различных соединений четырехполюсников.
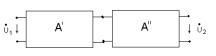
Каскадное соединение
|
|
Здесь выходные значения сигнала для первого четырехполюсника являются входными для второго. Происходит умножение матриц: |
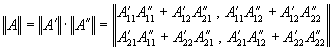 .
.
При
каскадном соединении симметричных
четырехполюсников складываются
постоянные передачи ![]() .
При одинаковых четырехполюсниках
.
При одинаковых четырехполюсниках ![]() .
.
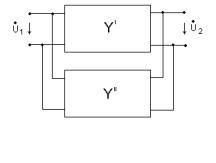
Параллельное соединение
|
|
При параллельном соединении складываются токи, следовательно, суммируются “Y”-матрицы:
|
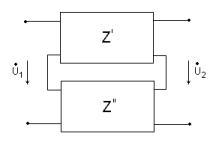
Последовательное соединение
|
|
Здесь складываются напряжения, следовательно, складываются “Z”-матрицы.
|
3.8. Передаточная функция и импульсная характеристика цепи
|
|
В радиотехнических цепях сопротивления нагрузки обычно велики и не влияют на четырехполюсник либо сопротивление нагрузки стандартно и уже учтено в схеме четырехполюсника. |
Тогда
четырехполюсник может характеризоваться
одним параметром, устанавливающим связь
между выходным и входным напряжениями
при пренебрежении током нагрузок. При
синусоидальном сигнале такой
характеристикой является передаточная
функция цепи (коэффициент передачи),
равная отношению комплексной амплитуды
сигнала на выходе к комплексной амплитуде
сигнала на входе: ![]() ,
где
,
где![]() –
фазово-частотная
характеристика,
–
фазово-частотная
характеристика, ![]() -амплитудно-частотная
характеристика цепи.
-амплитудно-частотная
характеристика цепи.
Передаточная
функция линейной цепи вследствие
справедливости принципа суперпозиции
позволяет анализировать прохождение
сложного сигнала через цепь, разлагая
его на синусоидальные составляющие.
Другой возможностью использования
принципа суперпозиции является разложение
сигнала на сумму сдвинутых во
времени d-функций d(t).
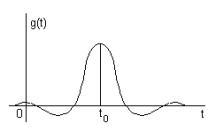
Реакцией цепи на действие сигнала в
виде d-функций
являетсяимпульсная
характеристика g(t), т.
е. это сигнал на выходе, если сигнал на
входе есть d-функция. ![]() при
при ![]() .
При этом g(t)
= 0 при t <
0 – выходной сигнал не может возникнуть
ранее момента появления входного
сигнала.
.
При этом g(t)
= 0 при t <
0 – выходной сигнал не может возникнуть
ранее момента появления входного
сигнала.
Экспериментально импульсную характеристику можно определить подавая на вход короткий импульс площадью единица и уменьшая длительность импульса при сохранении площади до тех пор, пока сигнал на выходе перестанет изменяться. Это и будет импульсная характеристика цепи.
Так как независимый параметр, связывающий напряжения на выходе и входе цепи, может быть только один, то между импульсной характеристикой и передаточной функцией имеется связь.
Пусть
на вход подается сигнал в виде d-функции ![]() со
спектральной плотностью
со
спектральной плотностью ![]() .
На выходе цепи будет импульсная
характеристика
.
На выходе цепи будет импульсная
характеристика ![]() ,
при этом все спектральные составляющие
входного сигнала умножаются на
передаточную функцию соответствующей
частоты:
,
при этом все спектральные составляющие
входного сигнала умножаются на
передаточную функцию соответствующей
частоты: ![]() .
Таким образом, импульсная характеристика
цепи и передаточная функция связаны
преобразованием Фурье:
.
Таким образом, импульсная характеристика
цепи и передаточная функция связаны
преобразованием Фурье:
![]() .
Иногда вводят так называемую переходную
характеристику цепи h(t),
являющуюся откликом на сигнал, называемый
единичным скачком:
.
Иногда вводят так называемую переходную
характеристику цепи h(t),
являющуюся откликом на сигнал, называемый
единичным скачком:
|
|
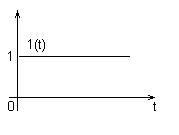
I(t) = 1 при t ³ 0 I(t) = 0 при t < 0 |
при
этом 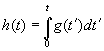 , h(t)
= 0 при t <
0.
, h(t)
= 0 при t <
0.
Ввиду связи между передаточной функцией и импульсной характеристикой, на передаточную функцию накладываются ограничения:
· Условие,
что g(t)
должна быть вещественной, приводит к
требованию, что ![]() ,
т. е. модуль передаточной функции (АЧХ)
есть четная, а фазовый угол (ФЧХ) –
нечетная функция частоты.
,
т. е. модуль передаточной функции (АЧХ)
есть четная, а фазовый угол (ФЧХ) –
нечетная функция частоты.
· Условие,
что при t <
0, g(t)
= 0 приводит к критерию Пэли-Винера: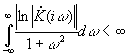 .
.
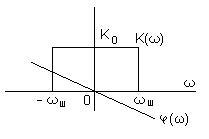
Например,
рассмотрим идеальный фильтр низких
частот ФНЧ с передаточной функцией 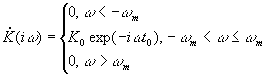 .
.
|
|
|
Здесь
интеграл в критерии Пэли-Винера
расходится, как и для любой![]() ,
обращающейся в нуль на конечном отрезке
оси частот.
,
обращающейся в нуль на конечном отрезке
оси частот.
Импульсная характеристика такого фильтра есть
![]() ,
,
g(t)
не равна нулю при t <
0, тем сильнее, чем меньше время задержки ![]() ,
которое определяет ее угол наклона
,
которое определяет ее угол наклона ![]() .
Это указывает на нереализуемость
идеального ФНЧ, имеющего близкое
приближение при достаточно больших
.
Это указывает на нереализуемость
идеального ФНЧ, имеющего близкое
приближение при достаточно больших ![]() .
.