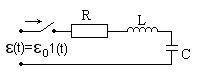
Включение цепи r, l, c под постоянное напряжение

Пусть в момент времени t = 0 включается постоянное ЭДС  на цепь R, L, C с нулевыми начальными условиями, т. е.I(0) = 0;  .

     Запишем II уравнение Кирхгофа для мгновенных значений напряжения:

 .

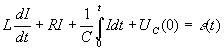Дифференцируя обе части, получим уравнение второго порядка для тока:

 .

Обозначив   для соответствующего однородного уравнения, получим  . Характеристическое уравнение   имеет корни  , решение однородного уравнения:   Общее решение неоднородного уравнения есть  , где   - ток установившегося режима (частное решение). В нашем случае  , т. к. постоянный ток через емкость пройти не может. Постоянные  найдем из начальных условий:  ;

  ,

т. к.  .

Тогда  ;     .

При  , т. е.  ,  ;  ,

 .

     Применим к этой задаче операторный метод.

При    ,    ,    ,

 .

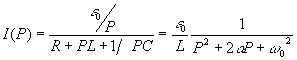Корни знаменателя  . Найдем вычеты от функции  , имеющей два полюса первого порядка:

 .

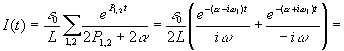
Наглядно видное преимущество операторного метода особенно проявляется при расчете сложных цепей.

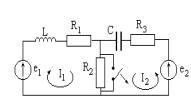
Размыкание ключом части сложной цепи

Пусть   . В момент t = 0 размыкается ключ и вместо него подключается сопротивление

     Составим уравнения для двух контуров по методу контурных токов в операторной форме.

 .

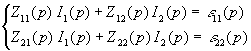Здесь  ,

 ,

 ,  ,     .

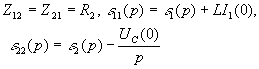Начальные значения тока  в индуктивности и напряжения на емкости

 ,         ,

        .

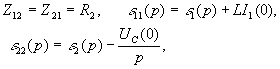
     Начальные значения тока в индуктивности и напряжения на емкости определяются при замкнутом ключе, так как при его размыкании они изменяться не могут.   определяется непосредственно. Для комплексной амплитуды напряжения на емкости можно получить:

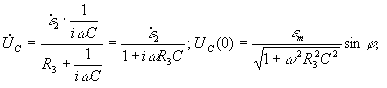  где

 ,

или  , т. к. 

Решив систему уравнений для контурных токов получим:

 ; , где .

Подставляя сюда значения операторных образов, сопротивлений и ЭДС, получим, например, следующие выражения для тока  :

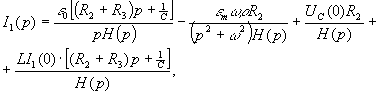
где  .

    В полученном выражении для   первые два члена определяют ток в переходном процессе при включении цепи под действием ЭДС е₁ и е_2.Последние два члена определяют ток переходного процесса, возникающего в цепи за счет ненулевых начальных значений тока в индуктивности Lи напряжения на конденсаторе С. Для перехода к временной зависимости тока с помощью вычетов необходимо найти нули знаменателей:  определяются решением уравнения .

 .

При вычислении вычетов от рациональных дробей выражения  значения нулей знаменателя  поочередно подставляются в числители и производные знаменателей:

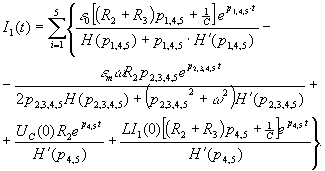
3.7. Четырехполюсники

Четырехполюсником называют электрическую цепь, имеющую два ввода и два вывода.

     Четырехполюсники и цепи, состоящие из нескольких четырехполюсников, являются основой тракта передачи и преобразования сигналов, несущих информацию. Теория четырехполюсников дает возможность единым методом анализировать системы, самые различные по структуре и принципу действия.

     Четырехполюсники называются активными, если внутри них содержатся источники энергии, и пассивными, если в них нет источников энергии. Активный четырехполюсник может быть заменен эквивалентным ему пассивным и вынесенными за зажимы последнего эквивалентными ЭДС. Рассмотрим параметры четырехполюсников при установившихся синусоидальных токах. Несинусоидальные токи могут быть разложены с помощью преобразования Фурье на гармонические составляющие. Установим зависимости, связывающие между собой входные и выходные напряжения и токи:  В зависимости от того, какая пара из них будет заданной, можно записать шесть различных по форме, но эквивалентных по существу пар уравнений, связывающих эти четыре величины. Более всего распространены 4 системы уравнений четырехполюсника, в каждой из которых используются четыре параметра. При указанных на схеме направлениях токов эти системы будут иметь вид:

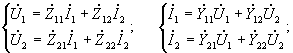
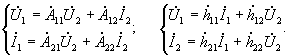
Все системы параметров выражаются друг через друга, например: ;  ;  ;  .

     Иногда направление тока   при рассмотрении четырехполюсника не как части тракта передачи сигнала, а как самостоятельной части сложной цепи меняют на противоположное к четырехполюснику. При этом параметры четырехполюсника     , стоящие коэффициентами при токе  , меняют знак.

     Заметим, что параметры   имеют размерность сопротивления, параметры   - размерность проводимости, параметры   - различные размерности:   - сопротивления,   - проводимости,  - безразмерные.

     Для пассивных четырехполюсников выполняется принцип взаимности, устанавливающий связь между входными и выходными напряжениями и токами, а следовательно и между параметрами четырехполюсника:

  либо  либо  .

Таким образом, независимыми остаются только три компонента. Докажем записанное соотношение для параметров  . Замкнем накоротко выход, и для тока на выходе получим:  , т. к.  , теперь перенесем источник питания из входной цепи, закоротив ее, в выходную цепь. Получим из системы уравнений  , т. к.  . Но, согласно принципу взаимности, эти токи должны быть равны по величине и направлению, а с учетом указанных на схеме направлений  , что и приводит к соотношению  , т. к. источник тот же самый.

     Другим упрощением является симметричный четырехполюсник, одинаковый по отношению к входным и выходным выводам. Перенося источник при разомкнутых противоположных выводах и меняя направления токов, из уравнений для Z-параметров можно получить , при этом  .

     Симметричный пассивный четырехполюсник имеет независимыми всего два параметра.

    Входные сопротивления четырехполюсника – это отношение   при заданном сопротивлении нагрузки   легко определяемые экспериментально. В качестве таких параметров применяют:

     1) сопротивление холостого хода   при разомкнутой выходной цепи. Разделив уравнения для параметров А первое на второе при  , получим  ;

     2) сопротивление короткого замыкания   при замкнутой выходной цепи, т. е. при  . Тогда  .

     Для симметричного пассивного четырехполюсника этих двух параметров достаточно, т. к. существуют соотношения     .

     Для несимметричного пассивного четырехполюсника необходимы дополнительные измерения, например, отношение напряжений  при разомкнутой выходной цепи  , либо отношение  также при  , либо оба эти измерения, если четырехполюсник активный.

     Интересным параметром симметричного четырехполюсника является характеристическое сопротивление  , обладающее свойством повторности, т. е. если его включить на выход в качестве нагрузки, то входное сопротивление также окажется равным характеристическому. Полагая  , можно получить:   и при        .

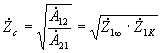     Совместным с характеристическим сопротивлением параметром симметричного четырехполюсника является постоянная передачи, равная логарифму отношений входного и выходного напряжений при сопротивлении нагрузки, равном характеристическому:

 ,    , где

 (непер) - коэффициент затухания,   (децибел);

  - коэффициент фазы.

     Можно показать, что 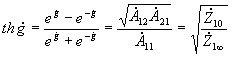 .