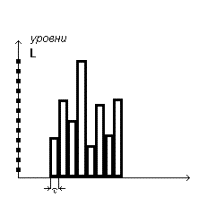
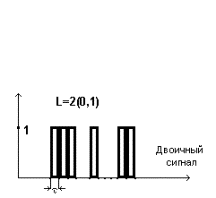
Информационная емкость дискретного и непрерывного сигналов

     Для двоичного сигнала имеем два равновероятных состояния  бит-информации при получении одного импульса. Количество полной информации в сообщении при длительности сигналаt_c (длительности передачи сообщения):   бит. Предельная скорость передачи информации, считая, что уровень сигнала существенно превышает уровень помех,  бит/сек. При числе возможных равновероятных уровней L:      бит, а предельная скорость передачи информации  , если разница между уровнями больше помехи.

Непрерывный сигнал

     Заменяем непрерывный сигнал дискретным с интервалом между выборками по Котельникову:  . При полной длительности сигнала   число выборок   Найдем максимально возможное число выборок L при наличии шума. Пусть  - средняя мощность сигнала,   - средняя мощность помехи (шума). Тогда 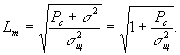  В этом случае информационная емкость сигнала

Разделив последнее выражение на  , получим предельную скорость передачи информации по Шеннону  Информационные возможности сигнала возрастают с расширением его спектра и превышением его уровня над уровнем помех.

Вопросы для самопроверки к главе II.

1. Покажите формы представления детерминированных сигналов.

2. Что представляет собой спектр периодического сигнала?

3. Чему равны комплексные амплитуды гармонических составляющих ряда Фурье?

4. Укажите характерные особенности АЧХ спектра периодической последовательности импульсов.

5. Напишите спектральную плотность прямоугольного импульса.

6. Как изобразить спектр видеоимпульса при амплитудной модуляции?

7. Какова связь между длительностью импульса и шириной его спектра?

8. Дайте определение девиации частоты и индекса угловой модуляции.

9. Характеризуйте спектр ЧМ сигнала при малых и больших индексах одноканальной модуляции.

10. Как определяется автокорреляционная функция сигнала и как она связана с его энергетическим спектром?

11. Как определяется амплитуда, угол и частота радиосигнала при одновременной, амплитудной и частотной модуляции?

12. Укажите типы импульсно-модулированных сигналов.

13. Покажите структуру спектра амплитудно-импульсного модулированного сигнала при однотональной модуляции.

14. Чему равен интервал дискретизации сигналов по Котельникову и как восстанавливается непрерывный сигнал по его отсчетам?

15. Напишите формулу Шеннона для предельной скорости передачи информации сигнала с шириной спектра f_max .

Задачи

1. Покажите, что ряд Фурье пилообразного колебания имеет вид: , где  .

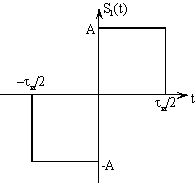
2. Найти спектральную плотность сигнала:

  при 

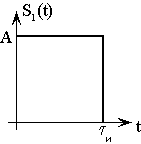
Ответ:  .

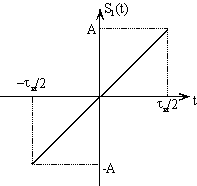
3. Найти спектральную плотность сигнала:

при  .   при  .

Ответ:  .

4. Найти спектральную плотность сигнала   при  .

Использовать формулу:  .

Ответ:  .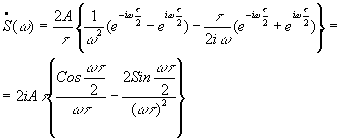

5. Найти спектральную плотность сигнала и его форму на выходе интегрирующей цепи:   при  .

Ответ:  .

6. Найти спектральную плотность сигнала:  при  .

Ответ:  .

7. Найти спектральную плотность сигнала   при  .

Указание: Использовать формулу:  .

Ответ:  .

8. Использовать ответы задач 1 и 7 подтвердите, что если периодическая последовательность образована повторением импульса s(t) с известной спектральной плотностью  , то комплексная амплитуда n-го члена ряда Фурье  , где Т – период последовательности,  - основная частота.

9. Найти спектральную плотность сигнала   при t>0.

Указание: Использовать формулу:  .

Ответ:  .

10. Имеется группа, состоящая из n одинаковых импульсов. Покажите, что спектральная плотность этой группы 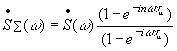 ,   -спектр одиночного импульса с длительностью  .

Указание: Воспользуйтесь свойством преобразования Фурье при сдвиге сигнала во времени и формулой суммирования геометрической прогрессии  .