2.8. Информация и сигнал. Информационная емкость сигналов Количественная оценка информации

     Получение информации всегда приводит к уменьшению неопределенности. Рассмотрим дискретный источник информации, характери-

зуемый дискретным набором (ансамблем) состояний с заданной вероятностью их появления: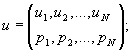    

     Меру неопределенности выбора состояния источника можно рассматривать как меру количества информации, получаемой при полном устранении неопределенности (т. е. содержащейся в источнике). Эта мера должна удовлетворять ряду естественных условий.

     1. Монотонное возрастание с увеличением возможности выбора(оценка по пятибалльной системе более полная, чем по двухбалльной).

     2. Аддитивность количества информации - неопределенность объединенного источника информации должна равняться сумме неопределенностей (а следовательно, и количества информации) исходных источников. Так, два независимых источника с числомравновероятных состояний n и m можно рассматривать как один источник, реализуемый пары состояний n_im_j с общим числом состояний N=mn, тогда   Это соотношение выполняется, если в качестве меры неопределенности источника с равновероятными состояниями принять логарифм числа состояний      Для другого примера аналогично: если каждое сообщение состоит из n символов, выбираемых из объема m, то число всех возможных сообщений   и, следовательно, , т. е. информация, полученная при выборке каждого из n символов, складывается.

     Основание логарифма определяет только масштаб или единицу количества информации, т. к. при N = 1   (одно состояние не имеет неопределенности), то минимальное количество информации будет при N = 2. Чтобы получить при этом единицу информации, основание логарифма приравнивают к 2 и такую единицу информации называют «бит» - информацию получаем при осуществлении одного из двух возможных состояний H = 1 бит при   N = 2 (Хартли, 1928). Предложенная мера количества информации применима только для равновероятных состояний:   тогда   информация, полученная при осуществлении i-го состояния.

     При неравновероятных состояниях свобода выбора источника ограничена, что должно привести к уменьшению неопределенности (и количества информации). Так, если источник информации имеет два состояния с вероятностями 0,99 и 0,01, то неопределенность здесь значительно меньше, чем при равновероятных состояниях с вероятностями 0,5 и 0,5. Значит мера неопределенности должна зависеть от функции распределения вероятности случайной величины. Еще одно условие состоит в том, что мера неопределенности не должна зависеть от пути выбора состояния в ансамбле, в том числе и многоступенчатом по группам состояний. К. Шенноном высказано утверждение, а Л. Я. Хинчиным математически доказано, что единственный функционал, удовлетворяющий сформулированным условиям, есть  (Шеннон, 1946 г). Сравнивая это выражение с выражением Хартли   для равновероятных состояний, видим, что при разных вероятностях происходит усреднение количества информации по всем возможным состояниям.

     Выражение Шеннона совпадает с выражением Больцмана для энтропии физической системы. В частности, по второму закону термодинамики энтропия замкнутой системы молекул  , где m_N - общее число молекул, m_i - количество молекул со скоростями в интервале  , т. к.  - вероятность такого состояния. В обоих случаях величина H характеризует степень разнообразия состояний системы. Максимальное значение энтропии при равновероятных состояниях растет с ростом числа этих состояний. Энтропия объединения нескольких статистически независимых источников равна сумме энтропии исходных источников:

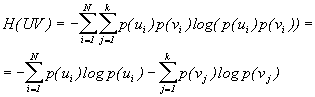
т. к. 

    

Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля.

     Для статистически зависимых ансамблей UV, описываемых совместной вероятностью,  где   - условная вероятность.

  где

 , 

  - условная энтропия.

     Энтропия объединения двух статистически связанных ансамблей U и  V равна безусловной энтропии одного ансамбля плюс условная энтропия другого относительно первого.

     Энтропия непрерывного источника информации бесконечна, т. к. неопределенность выбора из бесконечно большого числа возможных состояний бесконечно велика.

     Производя предельный переход в формуле Шеннона

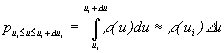 , получим

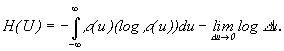
Вторая часть бесконечна, но она не зависит от плотности вероятности. Первая часть называется дифференциальной энтропией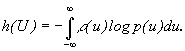  Ее можно трактовать как среднюю неопределенность выбора случайной величины U по сравнению со средней неопределенностью выбора случайной величины, изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение.

     При статистически связанных непрерывных источниках, дифференциальная условная энтропия

  

Дифференциальная энтропия зависит от масштаба (единицы измерения). Для непрерывного источника информации, ввиду бесконечности его меры неопределенности, понятие количества информации имеет несколько подходов. Наиболее простой из них - замена непрерывного сообщения дискретным с интервалом дискретизации по Котельникову  что позволяет полностью восстановить непрерывное сообщение, а следовательно, не потерять информацию.

     Прямой же подход определяет количество информации как разность априорной и апостериорной дифференциальной энтропии, последняя не равна нулю из-за некоторой неопределенности, оставшейся после регистрации события вследствие помех и конечной величины точности регистрации. При таком определении количества информации исчезает бесконечность после вычитания постоянного бесконечного члена.