
Бесконечно малая величина
Последовательность
an
называется бесконечно
малой, если
![]() .
Например, последовательность чисел
.
Например, последовательность чисел
![]() —
бесконечно малая.
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки
x0,
если
![]() .
.
Функция
называется бесконечно
малой на бесконечности,
если
![]() либо
либо
![]() .
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
![]() ,
то f(x)
− a
= α(x),
,
то f(x)
− a
= α(x),
![]() .
.
Бесконечно большая величина
Во всех
приведённых ниже формулах бесконечность
справа от равенства подразумевается
определённого знака (либо «плюс», либо
«минус»). То есть, например, функция
xsinx,
неограниченная с обеих сторон, не
является бесконечно большой при
![]() .
.
Последовательность
an
называется бесконечно
большой, если
![]() .
.
Функция
называется бесконечно
большой в окрестности точки
x0,
если
![]() .
.
Функция
называется бесконечно
большой на бесконечности,
если
![]() либо
либо
![]() .
.
19
Основные правила дифференцирования. Сумма.
Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х0 обозначаются для краткости так: u(х0) = u, v(х0) = v, u'(х0) = u', v'(х0)=v`. Если функции u и v дифференцируемы в точке х0, то их сумма дифференцируема в этой точке и
(u+v)' = u' + v'.
Коротко говорят: производная суммы равна сумме производных. 1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х0+Δx)+ v(х0+Δx) – (u(х0)+v(х0)) = (u(х0+Δx)-u(х0)) + (v(х0+Δx)-v(х0)) = Δu + Δv 2)
![]()
3) Функции u и v дифференцируемы в точке х0, т. е. при Δх→0
![]()
Тогда
![]()
при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’ Лемма. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е.
f(х0 + Δх)→f (х0) при Δx→0
. Действительно,

при Δх→0, так как
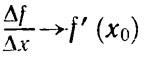
Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х0 + Δx)→f (х0) при Δх→0.
|
20
Пусть функция
![]() задана
на некотором интервале
задана
на некотором интервале
![]() .
Если найдётся такая функция
.
Если найдётся такая функция
![]() ,
что при всех
,
что при всех
![]() имеет
место равенство
имеет
место равенство
![]()
то функция
![]() называется
первообразной
для функции
называется
первообразной
для функции
![]() .
.
Пример
1.1
Рассмотрим функцию
![]() на
всей числовой оси
на
всей числовой оси
![]() --
на интервале
--
на интервале
![]() .
Тогда функция
.
Тогда функция
![]() --
это первообразная для
--
это первообразная для
![]() на
на
![]() .
.
Для
доказательства найдём производную от
![]() :
:

Поскольку равенство
верно при всех
![]() ,
то
,
то
![]() --
первообразная для
--
первообразная для
![]() на
на
![]() .
.
Аналогичное
определение дадим и для случая, когда
функция
![]() задана
не на одном интервале, а на объединении
нескольких непересекающихся интервалов:
задана
не на одном интервале, а на объединении
нескольких непересекающихся интервалов:

Назовём
функцию
![]() первообразной
для
первообразной
для
![]() ,
если при всех
,
если при всех
![]() выполнено
равенство
выполнено
равенство
![]() .При
изучении первообразной будем опираться
на следующее утверждение. Признак
постоянства функции: Если на промежутке
J производная Ψ(х) функции равна 0, то на
этом промежутке функция Ψ(х) постоянна.
.При
изучении первообразной будем опираться
на следующее утверждение. Признак
постоянства функции: Если на промежутке
J производная Ψ(х) функции равна 0, то на
этом промежутке функция Ψ(х) постоянна.
Это утверждение можно продемонстрировать геометрически.
Известно, что Ψ`(х)=tgα, γде α-угол наклона касательной к графику функции Ψ(х) в точке с абсциссой х0. Если Ψ`(υ)=0 в любой точке промежутка J, то tgα=0 δля любой касательной к графику функции Ψ(х). Это означает, что касательная к графику функции в любой его точке параллельна оси абсцисс. Поэтому на указанном промежутке график функции Ψ(х) совпадает с отрезком прямой у=С.
Итак, функция f(х)=с постоянна на промежутке J, если f`(х)=0 на этом промежутке.
Действительно, для произвольного х1 и х2 из промежутка J по теореме о среднем значении функции можно записать: f(х2)- f(х1)=f`(с) (х2- х1), т.к. f`(с)=0, то f(х2)= f(х1)
21
Опр.10.2.
Множество первообразных функции f(x)
называется неопределённым интегралом
от этой функции и обозначается символом
![]() .
.
![]() Как
следует из изложенного выше, если F(x)
- некоторая первообразная функции f(x),
то
Как
следует из изложенного выше, если F(x)
- некоторая первообразная функции f(x),
то
![]() ,
где C
- произвольная постоянная. Функцию f(x)
принято называть подынтегральной
функцией, произведение f(x)
dx
- подынтегральным выражением.
,
где C
- произвольная постоянная. Функцию f(x)
принято называть подынтегральной
функцией, произведение f(x)
dx
- подынтегральным выражением.
![]() Свойства
неопределённого интеграла,
непосредственно следующие из определения:
Свойства
неопределённого интеграла,
непосредственно следующие из определения:
-
 .
. -
 (или
(или
 ).
).
