53 Какие двойственные задачи линейного программирования назы-

ваются несимметричными? Как осуществляется сведение несимметричной

пары задач к симметричной?

Несимметричные двойственные задачи линейного программирования:

Задача L	Задача M

или

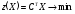
Они отличаются от симметричных тем, что:

1. Все ограничения в задаче L имеют вид уравнений, в то время как в симметричной паре в 1-й задаче это неравенства;

2. В задаче M отсутствуют условия неотрицательности неизвестных; таким образом неизвестные могут быть любого знака

Ответ на второй вопрос м.б. на Стр. 347 оранжевого учебника

54. Какова общая постановка взаимно двойственных задач? Сформулируйте основную теорему о взаимно двойственных задачах.

Рассмотрим на примере Двойственной задачи к задаче оптимального использования ресурсов.

Математическая модель ЗЛП

II производитель хочет перекупить сырье. Каковы оптимальные условия продажи сырья?

II выгодно минимизировать затраты на покупку сырья.

I выгодно продавать сырье, если общая стоимость сырья, расходуемого на каждое изделие не меньше прибыли от продажи этого изделия.

55. Постановка транспортной задачи как задачи линейного программирования. Закрытая и открытая модель транспортной задачи. Приведите примеры.

Классическая транспортная задача ЛП формулируется следующим образом.

            Имеется  m  пунктов производства (поставщиков) и n  пунктов

потребления (потребителей) однородного продукта. Заданы величины:

 - объем производства (запас) i-го поставщика,  i=1, m  ;

 - объем потребления   (спрос) j-го потребителя, i=1, n ;

  - стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к  j-му потребителю.

            Требуется составить такой план перевозок, при котором спрос

всех потребителей был бы выполнен и при этом общая стоимость всех

перевозок была бы минимальна.

            Математическая модель транспортной задачи имеет вид

                       

Обычно исходные данные записываются в виде таблицы:

Модель транспортной задачи называется закрытой, если , то есть

суммарные запасы поставщиков равны суммарным запросам потребителей.

Если ,то такая модель транспортной задачи называется открытой.

Открытая модель решается приведением к закрытой.

            В случае, когда суммарные запасы превышают суммарные

потребности, т.е.

                                              

вводится фиктивный n+1 потребитель, потребности которого

                                              

В случае, когда суммарные потребности превышают суммарные

запасы,  т.е.

                                              

, вводится фиктивный m+1 поставщик, запасы которого

                                              

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика

полагают равными нулю, так как груз в обоих случаях не перевозится.

Пример закрытой модели:

Поставщики	Потребители				Запасы
	2	4	5	40
	3	5	8	60
Потребности	20	30	50	100

Пример открытой модели:

Поставщики	Потребители				Запасы
	2	4	5	70
	3	5	8	60
Потребности	70	60	50	130 180

56. Докажите, что ранг системы нетривиальных ограничений транспортной задачи m ╳ n равен m + n –1.

Ранг матрицы системы ограничений транспортной задачи равен

Доказательство. Если к последней строке матрицы прибавить (n-1) строк, начиная с (m+1) ‑й, и вычесть первые m строк, то получится строка, состоящая из нулей. Следовательно, ранг матрицы ограничений