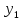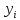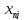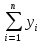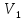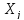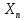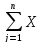- •4. Запишите структурную таблицу и поясните уравнение межотраслевого баланса для межотраслевой экономики; укажите экономический смысл входящих в уравнение величин.
- •6. Дайте определение и приведите пример продуктивной матрицы, обоснуйте продуктивность приведённой матрицы.
- •14. Задача о диете.
- •15. Задача об использовании ресурсов
- •Транспортная задача
- •21. Сформулируйте и докажите теорему о существовании решения задачи линейного программирования в случае ограниченной целевой функции
- •23. Сформулируйте и докажите теорему о достижимости оптимального решения на выпуклой линейной комбинации оптимальных угловых точек.
- •24. В чем состоит графический метод решения задачи лп в случае
- •30. Опираясь на алгоритм графического метода, постройте злп с
- •31.Опираясь на алгоритм графического метода, постройте злп на
- •32. Каковы основные предпосылки для применения симплекс-
- •33. 34. Изложите и обоснуйте алгоритм решения задачи линейного программирования симплекс-методом.
- •35. Как по симпплекс-таблице можно сказать:
- •36. Как по симплекс-таблице задачи линейного программирования можно сказать: а) допустимое решение оптимально; б) есть альтернативное решение. Приведите примеры.
- •37. Является ли симплекс-таблица для злп на минимум окончательной? Ответ обоснуйте. Найдите решение злп или сделайте вывод о неразрешимости задачи.
- •38. Является ли симплекс-таблица для злп на минимум окончательной? Ответ обоснуйте. Найдите решение злп или сделайте вывод о неразрешимости задачи.
- •42. Является ли симплекс-таблица для злп на максимум окончательной? Ответ обоснуйте. Найдите решение злп или сделайте вывод о неразрешимости задачи.
- •43. Является ли симплекс-таблица для злп на максимум окончательной? Ответ обоснуйте. Найдите решение злп или сделайте вывод о неразрешимости задачи.
- •44. Является ли симплекс-таблица для злп на максимум окончательной? Ответ обоснуйте. Найдите решение злп или сделайте вывод о неразрешимости задачи.
- •45. Как найти допустимый базис в злп? Алгоритм метода искусственного базиса.
- •46. Всегда ли можно найти допустимый базис в задаче линейного программирования?
- •47. Теорема о конечности симплекс-метода для невырожденной задачи лп.
- •49. Постановка взаимно-двойственных задач. Поясните (можно на примере) экономическую суть понятия двойственности.
- •51. Сформулируйте основную теорему двойственности для симметричных задач. Какой критерий оптимальности решения вытекает из этой теоремы?
- •52. Сформулируйте и докажите теорему равновесия для двойственных задач.
- •53 Какие двойственные задачи линейного программирования назы-
- •57. Сформулируйте и докажите критерий разрешимости транспортной задачи.
- •59. Опишите схему решения транспортной задачи методом потенциалов. Приведите пример.
- •60. Сформулируйте определения следующих понятий: свободная
- •Обоснуйте метод потенциалов с помощью основных теорем двойственности.
- •Постановка задачи о кратчайшем пути. Приведите пример.
- •63)Алгоритм Дейкстры поиска кратчайшего маршрута на графе.
- •64)Применим ли алгоритм Дейкстры поиска кратчайшего пути в
- •65.Постановка задачи о максимальном потоке в сети.
- •66.Алгоритм Форда-Фалкерсона решения задачи о максимальном потоке в сети. Приведите пример.
-
Числом Фробениуса неотрицательной матрицы называется наибольшее собственное значение этой матрицы. Он удолетворяет условию:

Вектором Фробениуса называется собственный вектор, соответствующий числу Фробениуса. Ищем из условия:

2)
Теорема
(Фробениуса-Перрона).
У "
матрицы А³0
$
собственное значение (называемое
числом Фробениуса)
такое, что

-
вектор
Фробениуса.


Причем, если А>0, то и
Теорема:
есть
вектор Фробениуса A.

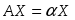
Доказательство: пусть
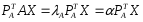

3) Теорема
Число Фробениуса A ³ 0 удовлетворяет
Условию: m
≤
 ≤ M
≤ M
Доказательство:
Пусть
 :
:
 =
1.
=
1.


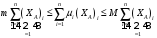
 m
≤
m
≤
 ≤ M
≤ M
4. Запишите структурную таблицу и поясните уравнение межотраслевого баланса для межотраслевой экономики; укажите экономический смысл входящих в уравнение величин.
|
Отрасли |
1 |
2 |
… |
j |
… |
n |
Итого |
Конечная продукция |
Валовая продукция |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
|
|
|
|
Условно чистая продукция |
|
|
|
|
|
|
|
|
|
|
Валовая продукция |
|
|
|
|
|
|
|
|
|
X = АX + Y, (1)

 ,
≥0
,
≥0
 ≥0
≥0
Вектор X называется вектором валового выпуска, вектор Y – вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (1) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов X и Y это соотношение называют также моделью Леонтьева.
5. В чем заключается гипотеза линейности для переменных структурной таблицы межотраслевой экономики? Запишите формулу вычисления элементов матрицы Леонтьева и уравнение линейного межотраслевого баланса (модель Леонтьева).
В. Леонтьев
рассматривая развитие американской
экономики в 30-е годы ХХ века, обратил
внимание на важное обстоятельство. А
именно величины
 ij
=
ij
=
 остаются постоянными в течение ряда
лет. В соответствии со сказанным сделаем
такое допущение: для выпуска любого
объема хj продукции отрасли j необходимо
затратить продукцию отрасли i в количестве
аij хj, где аij – постоянный коэффициент.
Проще говоря, материальные издержки
пропорциональны объему производимой
продукции. Это допущение постулирует
линейность существующей технологии.
Принцип линейности распространяют и
на другие виды издержек (например, на
оплату труда), а также на нормативную
прибыль.
остаются постоянными в течение ряда
лет. В соответствии со сказанным сделаем
такое допущение: для выпуска любого
объема хj продукции отрасли j необходимо
затратить продукцию отрасли i в количестве
аij хj, где аij – постоянный коэффициент.
Проще говоря, материальные издержки
пропорциональны объему производимой
продукции. Это допущение постулирует
линейность существующей технологии.
Принцип линейности распространяют и
на другие виды издержек (например, на
оплату труда), а также на нормативную
прибыль.
Итак, согласно гипотезе линейности имеем
хij = аijхi (i, j = 1, …, n). (1)
Коэффициенты аij называют коэффициентами прямых затрат (коэффициентами материалоемкости).
Подставляя соотношения (1) в уравнение баланса хi = хi1 + хi2 + … + хin + уi, получаем систему n линейных уравнений относительно переменных х1, х2,…, хn:
х1 = а11х1 + а12х2 + … а1nхn + у1,
х2 = а21х1 + а22х2 + … а2nхn + у2,
…………………………………..
хn = аn1х1 + аn2х2 + … аnnхn + уn,
или, в матричной записи,
X = АX + Y, (2)

 ,
≥0
,
≥0
 ≥0
≥0
Вектор X называется вектором валового выпуска, вектор Y – вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (2) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов X и Y это соотношение называют также моделью Леонтьева.