Міністерство освіти і науки України

Національний університет водного господарства та природокористування

Кафедра електротехніки і автоматики

ЗВІТ

навчальної практики

з програмування і комп’ютерної техніки

Варіант 11

Виконав:

студент I курсу

групи АУТП-13

Михайлюк Дмитро

Перевірив:

Клепач М. М .

Рівне-2010

Зміст

1. Повне дослідження функції та побудова її графіка.

2. Розв‘язування задачі для обчислення матриць засобами мови програмування С++ та засобами Microsoft Excel.

3. Створення бази даних засобами MS Access.

4. Розробка програми для роботи зі структурами та файлами даних засобами мови програмування С++.

5. Сканування та розпізнавання документів.

6. Використана література.

Мета:

Метою практики є засвоєння студентами навиків практичного використання знань, набутих при вивченні навчальних дисциплін “Алгоритмізація і програмування” та “Комп’ютерна техніка і організація обчислювальних робіт”.

Завданням практики є рішення задач зв’язаних з комплексним використанням персонального комп’ютера, включаючи створення програм на одній з мов програмування, роботу з електронними таблицями, текстовими редакторами, системами управління базами даних, роботу у всесвітній комп’ютерній мережі Internet.

Програма роботи:

І Повне дослідження функції та побудова її графіка.

ІІ. Розв‘язування задачі для обчислення матриць засобами мови програмування С++ та засобами Microsoft Excel.

ІІІ. Створення бази даних засобами MS Access.

IV. Розробка програми для роботи зі структурами та файлами даних засобами мови програмування С++.

V. Сканування та розпізнавання документів.

Завдання №1 Повне дослідженя функції

1. Аналітично провести повне дослідження функції.

2. Побудувати графік функції засобами програми Microsoft Excel. На графіку вказати характерні точки для функції (максимуму, мінімуму, перегину, перетину з осями координат), зобразити асимптоти функції (якщо вони є).

3. Написати програму мовою С++ для побудови графіка функції. На графіку вказати характерні точки для функції (максимуму, мінімуму, перегину, перетину з осями координат), зобразити асимптоти функції (якщо вони є).

4. Порівняти отримані результати у п. 1, п. 2 та п. 3. Зробити висновки.

5. В редакторі Microsoft Word описати проведені дослідження, вставити графіки функції, побудовані засобами Microsoft Excel та засобами мови програмування С++, виконати їх порівняльний аналіз.

Хід роботи:

1.Визначення області допустимих значень

0

2.Точки перетину з осями

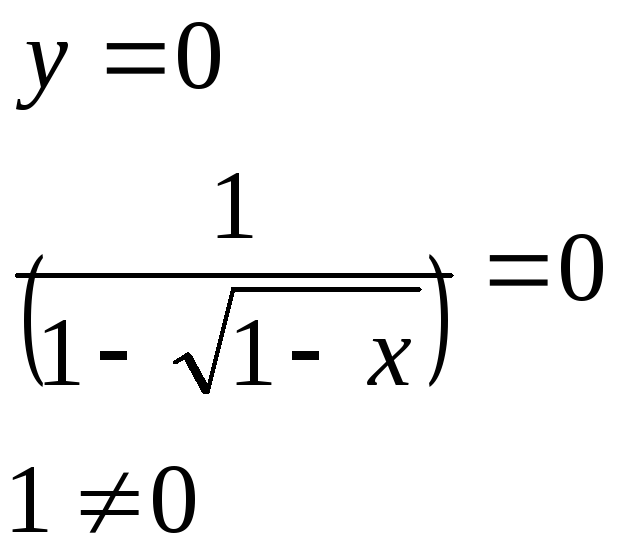
Графік не перетинає вісь Ох.

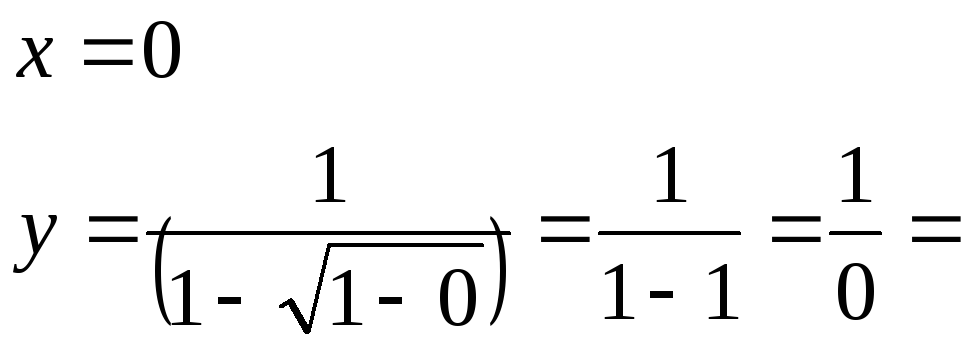
Графік не перетинає вісь Оу.

3. Функція неперіодична.

Функція періодична, якщо при будь-яких

, де - період функції.

Нехай , а , тоді

Отже, функція неперіодична.

4. Парність (непарність)

Функція називається парною, якщо

Отже, функція ні парна, ні непарна.

5. Точки розриву функції

Оскільки в т не визначені границі, то дана точка є точкою розриву 2 роду.

6.Проміжки зростання і спадання

Відрізок [-12;-0,5]

З графіка видно, що більшим значенням х відповідає менше значення у, отже цей відрізок є спадаючим.

Доведення:

Якщо функція спадає на [-12;-0,5], то її похідна

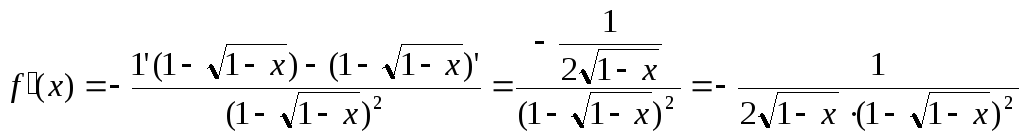
, те що і потрібно було довести.

Відрізок [0;1]

Доводиться аналогічно.

7.

, отже функція не має точок екстремуму.

8. Проміжки опуклості та ввігнутості, точки перегину графіка функції.

Графік функції на інтервалі ввігнутий, якщо він лежить вище будь-якої дотичної, проведеної до графіка функції на інтервалі . З Графіка видно що обидві частини графіка є увігнутими.

9. Будуємо графік

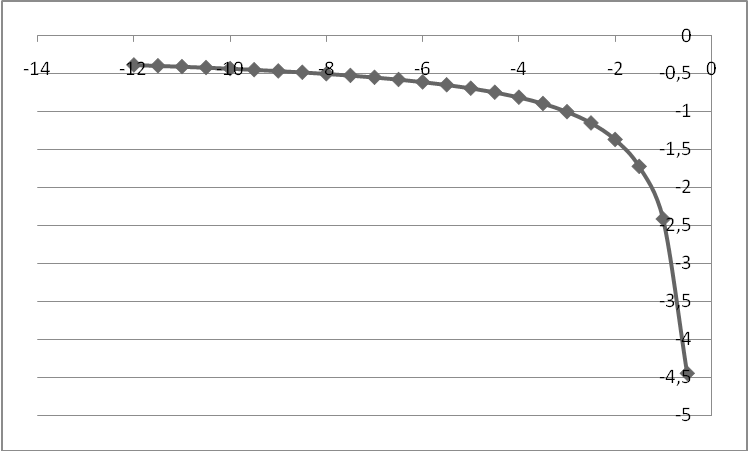
Результат в Excel

f(x)	x	∆x
-0,3838	-12	0,5
-0,39439	-11,5
-0,40583	-11
-0,41821	-10,5
-0,43166	-10
-0,44635	-9,5
-0,46248	-9
-0,48026	-8,5
-0,5	-8
-0,52206	-7,5
-0,54692	-7
-0,57517	-6,5
-0,60763	-6
-0,64537	-5,5
-0,6899	-5
-0,74338	-4,5
-0,80902	-4
-0,89181	-3,5
-1	-3
-1,14833	-2,5
-1,36603	-2
-1,72076	-1,5
-2,41421	-1
-4,44949	-0,5

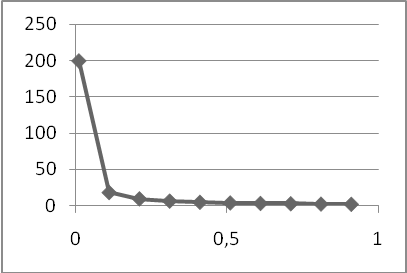
f(x)	x	∆x
199,4987	0,01	0,1
17,66726	0,11
8,994378	0,21
5,905363	0,31
4,312475	0,41
3,333333	0,51
2,663114	0,61
2,166925	0,71
1,772704	0,81
1,428571	0,91

Результат в Borland C++

//---------------------------------------------------------------------------

#include <vcl.h>

#pragma hdrstop

#include <math.h>

#include "Unit1.h"

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//---------------------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Button1Click(TObject *Sender)

{ float tum1=StrToFloat(Edit1->Text);

float tum2=StrToFloat(Edit2->Text);

float y;

for(float t=tum1; t<tum2; t++ )

{

Series1->Add(1/(1-sqrt(1-t)),t,clRed);}

Button1->Enabled=false;

Button2->Enabled=true;

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Button2Click(TObject *Sender)

{

exit(1);

}

//---------------------------------------------------------------------------

Результат скопійований з монітора

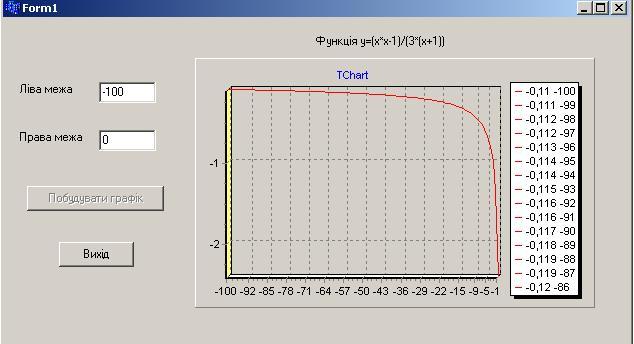
Висновок: Провівши повне дослідження функції, побудувавши графік функції засобами програми Microsoft Excel та C++ Builder я дійшов висновку, що аналіз функцій був проведений правильно і графіки повністю співпадають.