4. 1.2.Шифраторы.

Шифраторы – устройства, определяющие адрес направления, по которому поступил запрос.

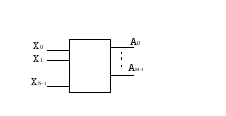
Рис.1.6.

Такое устройство имеет N входов (x₀ x_N-1 и M выходов (A₀ A_M-1). В каждый момент времени активным может быть только один вход. На выходах при этом появляется двоичная комбинация, соответствующая адресу активного входа. Очевидно, что M=log₂N –для полнодоступного шифратора и Mlog₂N - для неполнодоступного. Неполнодоступным шифратором называется устройство, имеющее количество входов не кратное степени двух.

В качестве примера построим шифратор на 4 входа.

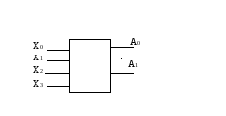
Рис.1.7.

Таблица функционирования такого устройства при условии активного уровня «1»

X3	X2	X1	X0	A1	A0
0	0	0	1	0	0
0	0	1	0	0	1
0	1	0	0	1	0
1	0	0	0	1	1

Табл.1.2.

Из таблицы выводим выражения для A₀ и A₁

A₀ =x₀  x₁x₂x₃  x_0 x₁x₂ x₃ =x₀x₂(x₁x₃);

A₁ = x₀ x₁ x₂x₃  x_0 x₁x₂ x₃ =x₀x₁(x₂x₃);

Строим схему

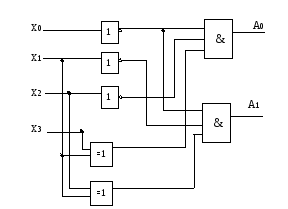
Рис.1.8.

5. 1.3.Дешифраторы.

Дешифратор – устройство, посылающее запрос по направлению, адрес которого установлен на входах. Такое устройство имеет N адресных входов (A₀A_N-1) и M выходов (y₀y_M-1).

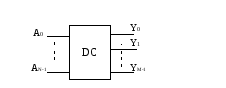
Рис.1.9.

В каждый момент времени активный уровень может появиться только на одном выходе, адрес которого в виде двоичной комбинации установлен на адресных входах. Для полного дешифратора количество выходов M=2^N , для неполного - M2^N .

В качестве примера рассмотрим синтез дешифратора на два адресных входа.

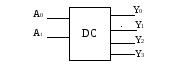
Рис.1.10.

Таблица функционирования при активном уровне «1».

A1	A0	Y3	Y2	Y1	Y0
0	0	0	0	0	1
0	1	0	0	1	0
1	0	0	1	0	0
1	1	1	0	0	0

Табл.1.3.

Из таблицы очевидно, что

y₀=A₀ A₁;

y₁= A₀ A₁

y₂=A₀  A₁;

y₃= A₀  A₁;

Построим схему.

Р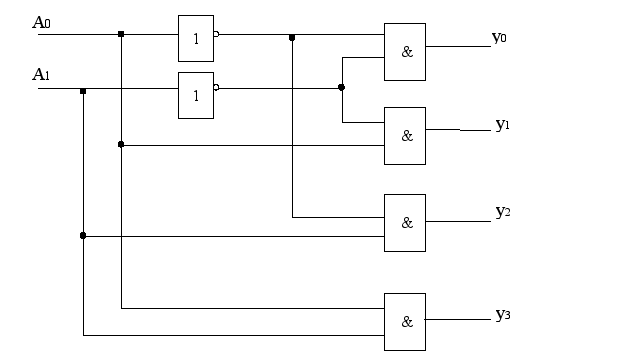ис.1.11.

6. 1.4. Кодопреобразователь.

К этому классу можно отнести все вышеперечисленные устройства, т.к. код на выходе этих устройств по определенному закону зависит от кода на входе. Но это специализированные кодопреобразователи. Если же мы хотим расширить возможности для функций преобразования необходимо синтезировать кодопреобразователи общего класса. В таком устройстве также задается таблица функционирования, записываются выражения для каждого выхода и по ним строится схема.

В качестве примера рассмотрим устройство на 4 входа, выдающее положительный результат при появлении не менее 3-х входных «1». Такой кодопреобразователь имеет только один выход. Таблица функционирования

X3	X2	X1	X0	Y
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

Табл.1.4.

Функция выхода

Y= x₀ x₁ x₂ x₃x₀ x₁ x₂ x₃  x₀x₁ x₂ x₃  x₀ x₁x₂ x₃  x₀ x₁ x₂x₃ = x₁ x₂ x₃ (x₀x₀)  x₀x₃(x₁x₂x₁x₂)  x₀x₁x₂x₃ = x₁x₂x₃x₀x₃(x₁x₂)x₀x₁x₂x₃ = x₁x₂(x₃x₀x₃)x₀x₃(x₁x₂) = x₁x₂(x₃x₀)x₀x₃(x₁x₂) (1.5)

При выводе выражения 1.5. учитываем, что x₀x₀ = 1, x₁x₂x₁x₂=x₁x₂, x₃x₀x₃=x₃x₀

Построим схему.

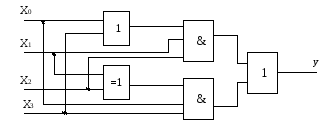
Рис.1.12.