2. Кусочно-постоянный оператор

Одномерный случай:

Исходные данные: координаты разбиения по X, значение параметра M в каждой области разбиения:

Рис 5.2.1 Исходные данные одномерного случая

Как видно, вычисление производится в два этапа – вычисление коэффициентов и вычисление функции, которая зависит от одного параметра. В N-мерных случаях, число коэффициентов и функций будет равно N.

подбирается таким образом, чтобы знаменатель не превращался в ноль, значение этой переменной никак не меняет результат.

Двумерный случай:

Рис 5.2.2 Исходные данные двумерного случая

Аналогично с одномерным случаем, исходными данными являются разбиение по осям, значение параметра в каждой области.

Коэффициент нужен только для расчета , и в дальнейших вычислениях он не используется.

В двумерном случае используются уже две матрицы параметров и две функции, одна зависит от обеих координат, другая вызывается в первой, и зависит от одной координаты.

Трехмерный случай:

Рис. 5.2.3. Исходные данные трехмерного случая

Следуя аналогиям с двумерным оператором, вычислим три - матрицы, первая из которых зависит от матрицы M, следующие зависят только от предыдущих.

Построим функции:

N-мерный случай,

Рассчитываем первую матрицу, использую значения исходной матрицы M:

Вторая матрица коэффициентов рассчитывается на основании первой.

Получили набор массивов коэффициентов, из которых нам потребуется только последний, .

Первая функция использует все координаты.

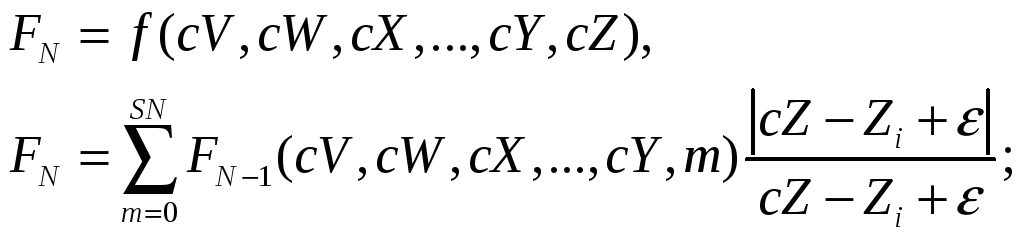
подбирается таким образом, чтобы знаменатель не превращался в ноль, значение этой переменной никак не меняет результат.

3. Реализация математической модели на языке C/C++

Поскольку созданный N-мерный оператор является сложным для вычисления даже простейших задач, целью этой работы также являлось создание программного комплекса, позволяющего решать поставленные задачи.

В качестве среды разработки был выбран язык c/c++, в силу некоторых причин, таких как работа с текстовыми файлами, возможность использования подключаемых модулей (dll), возможность создания собственного интерфейса взаимодействия между программой и пользователей.

Структура программы выглядит следующим образом:

Рис 4.3.1. Структурная схема программы

В качестве исходных данных выступают:

• Файлы с таблицами разбиения объекта по осям X,Y,Z.

• Файл с таблицей индексов материалов в каждом секторе разбиения.

• Файл с таблицей шкал температур

• Файл с таблицей коэффициентов каждого материала

После обработки данных в dll, высчитываются две главные переменные – матрица коэффициентов кусочно-линейного оператора:

И матрица для расчета значений кусочно-постоянного оператора.

Данные считываются в графический модуль программы, в котором происходят дальнейшие вычисления для отображения данных.

Создается сетка узлов, в которых будет высчитываться значение коэффициента теплопроводности в зависимости от температуры.

Программа имеет два режима отрисовки. В первом режиме для каждого видимого узла, показывается индекс его материала. В таком режиме можно проверить, насколько точно было проведено разбиение по координатам.

Второй режим предназначен для вывода информации о значении коэффициента теплопроводности. С помощью цветовой палитры для каждого узла обозначается его значение теплопроводности – чем темнее цвет, тем больше значение коэффициента теплопроводности.

Результаты программы отображены в главе «проведение эксперимента». Код кусочно-линейного и кусочно-постоянного операторов представлен в приложениях 1 и 2.