Закон Фарадея. Согласно закону электромагнитной индукции Фарадея (в системе си): где — электродвижущая сила, действующая вдоль произвольно выбранного контура,

  — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где  — электродвижущая сила, N — число витков, — магнитный поток через один виток,  — потокосцепление катушки.

Векторная форма. В дифференциальной форме закон Фарадея можно записать в следующем виде: (в системе си)

или с помощью простейшей эквивалентной формулы:

Здесь  — напряжённость электрического поля,  — магнитная индукция, C — произвольная площадка,  — её граница.

Следует отметить, что закон Фарадея в такой форме описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт вариации самого поля без изменения границ контура. Если магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС описывается силой Лоренца, хотя равенство  продолжает соблюдаться.

Закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля.

Потенциальная форма. При выражении магнитного поля через векторный потенциал, закон Фарадея принимает форму: (в отсутствие электростатического поля)

При учёте электростатического поля имеем:

48. Вихревые токи, токи Фуко (в честь Фуко, Жан Бернар Леон) — вихревые индукционные токи, возникающие в массивных проводниках при изменении пронизывающего их магнитного потока.

Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленцаони выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и др.

Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечниковтрансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.

49. Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления —электромагнитной индукции.При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока, созданного током первого проводника и проходящего через контур второго, что по закону электромагнитной индукциивызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью. Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.

Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении тока, протекающего через контур.

При изменении тока в контуре меняется магнитный поток через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи ЭДС препятствует возрастанию тока, а при уменьшении тока — убыванию.

Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L: .

За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажиганияавтомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25 кВ. Что не совсем верно: бросок тока в первичной обмотке, вызванный самоиндукцией, создаёт ЭМ-импульс, который и создаёт высокое напряжение на вторичной обмотке. Также это явление применяется для поджига люминесцентных ламп в стандартной схеме. Индукти́вность — коэффициент пропорциональности между магнитным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величиной этого тока.

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле. Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом: где L — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду: где  — сумма магнитных потоков через все витки, а L — уже индуктивность многовитковой катушки. Ψ называют потокосцеплением или полным магнитным потоком. Коэффициент пропорциональности L иначе называется коэффициентом самоиндукции контура или просто индуктивностью.

Если поток, пронизывающий каждый из витков одинаков, то Ψ = NΦ. Соответственно, LN = L1N2 (суммарный магнитный поток увеличивается в N раз и потокосцепление еще в N раз). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.

В системе единиц СИ индуктивность измеряется в генри, сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109 см). Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ L, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом  в феврале 1886 года[источник не указан 521 день].

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:.

При заданной силе тока индуктивность определяет энергию магнитного поля тока:.

Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности.

50. энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить: где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величинаравная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей. 

51. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Причина возникновения электрического тока в неподвижном проводнике - электрическое поле. Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток. Индукционное электрическое поле является вихревым. 

Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

электростатическое поле	индукционное электрическое поле ( вихревое электр. поле )
1. создается неподвижными электр. зарядами	1. вызывается изменениями магнитного поля
2. силовые линии поля разомкнуты - -потенциальное поле	2. силовые линии замкнуты - - вихревое поле
3. источниками поля являются электр. заряды	3. источники поля указать нельзя
4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0.	4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции

1)Электрический заряд и его свойства. Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е = 1,6×10-19 Кл). Электрон (me=9,11×10-31 кг), и протон(mp= 1,67×10 –27) являются соответственно носителями элементарных отрицательного и положительного зарядов. Одноименные заряды друг от друга отталкиваются, разноименные – притягиваются. Фарадей 1843г. установлен з-н сохранения электрического заряда:- алгебраическая сумма электрического заряда любой замкнутой системы остается неизменной, какие бы процессы  не происходили внутри этой системы. Электрический заряд – величина релятивистская инвариантная, т.е. не зависит от системы отсчета, а значит не зависит от того движется ли этот заряд или покоится. В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники. Проводники – тела, в которых электрический заряд может перемещаться по всему объему. Проводники делятся на 2 подгруппы: 1)проводники I-го рода (металлы) перенос в них зарядов не сопровождается химическими превращениями. 2)проводники II-го рода – перенос в них зарядов ведет к химическим изменениям(кислоты). Диэлектрики (стекло, пластмассы) – тела, в которых практически отсутствуют свободные заряды . Полупроводники – занимают промежуточное положение между проводниками и диэлектриками(кремний, германий). единица эл. заряда – Кл, производная единица, т.к. определяется через ток. 1 Кл – эл. заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1с. З-н Кулона. Точечным наз-ся заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заря-женных тел, с которыми он взаимодействует. сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам q1 и  q2 и обратно пропорциональна  квадрату расстояния r между ними: k – коэффициент пропорциональности, зависящий от выбора системы единиц.

2)Кулона закон, один из основных законов электростатики, определяющий силу взаимодействия между двумя покоящимися точечными электрическими зарядами, т. е. между двумя электрически заряженными телами, размеры которых малы по сравнению с расстоянием между ними. Установлен Ш. Кулоном в 1785 опытным путём с помощью изобретённых им крутильных весов. Согласно К. з., два точечных заряда взаимодействуют друг с другом в вакууме с силой F, величина которой пропорциональна произведению зарядов e1 и e2 и обратно пропорциональна квадрату расстояния r между ними:  (1)

Здесь k — коэффициент пропорциональности, зависящий от выбранной системы единиц; в абсолютной (гауссовой) системе единиц (СГС системе единиц)k = 1; в Международной системе единиц (СИ) k = 1/4pe0, где e0 —электрическая постоянная. Сила F направлена по прямой, соединяющей заряды, и соответствует притяжению для разноимённых зарядов (F << 0) и отталкиванию для одноимённых (F > 0).

Если взаимодействующие заряды находятся в однородном диэлектрике с диэлектрической проницаемостью е, то сила взаимодействия уменьшается в e раз:

 (2)

К. з. служит одним из экспериментальных оснований классической элетродинамики; его обобщение приводит, в частности, к т. Гаусса

К. з. называется также закон, определяющий силу взаимодействия двух магнитных полюсов:  (3)

Здесь f — коэффициент пропорциональности (в общем случае не совпадающий с k; в абсолютной системе единиц f = 1), m1, m 2 —магнитные заряды, m —магнитная проницаемость среды, окружающей взаимодействующие полюса. В вакууме  

3) Электрическое поле. Напряженность электрического поля.Закон Кулона не объясняет механизм передачи электромагнитного взаимодействия: близкодействие (непосредственный контакт) или дальнодействие? Если заряды действуют друг на друга на расстоянии, то скорость передачи взаимодействия должна быть бесконечно большой, взаимодействие должно распространяться мгновенно. На опыте скорость конечна (скорость света с=3.108м/с).

Для объяснения вводится понятие электрического поля (впервые - М. Фарадей) - особый вид материи, существующий вокруг любого электрического заряда и проявляющий себя в действии на другие заряды.  Напряженность - силовая характеристика электрического поля. 

Пусть заряд q0 создает поле, в произвольную точку которого мы помещаем положительный заряд q. Во сколько бы раз мы не изменяли заряд q в этой точке, сила взаимодействия изменится во столько же раз (з-н Кулона). Следовательно: - величина постоянная в данной точке данного поля.  Напряженность - векторная физическая величина, численно равная отношению силы, действующей на заряд, помещенный в данную точку данного поля, к величине этого заряда. Напряженность не зависит от величины заряда, помещенного в поле.

, если q>0. , если q<0. Т.е. вектор напряженности направлен от положительного заряда и к отрицательному. Напряженность в данной точке поля равна 1, если на заряд в 1 Кл, помещенный в эту точку, действует сила в 1 Н. (Напряженность равна 1 , если между точками электростатического поля, находящимися на расстоянии 1 м друг от друга, существует разность потенциалов 1 В).

Принцип суперпозиции полей: напряженность поля, созданного системой зарядов равна геометрической сумме напряженностей полей, созданных каждым зарядом. Т.е. напряженности складываются геометрически:  

Пример:

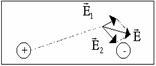
Графическое представление электростатического поля.Силовые линии (линии напряженности) - непрерывные (воображаемые) линии вектор напряженности касателен к каждой точке которых. Способ описания с помощью силовых линий введен Фарадеем. 

 

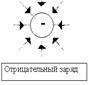
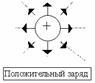
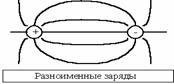
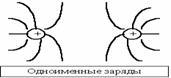
Свойства:  1. Начинаются на положительных и заканчиваются на отрицательных зарядах. 2. Не пересекаются.

3. Густота линий тем больше, чем больше напряженность. Т.е. напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности. Можно договориться изображать поля так, что количество проведенных линий пропорционально величине заряда.

4) Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:,

где Wп1 и Wп2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно

При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r1 и r2 от заряда Q,.

Если поле создано системой точечных зарядов Q1, Q2,, Qn, то изменение потенциальной энергии заряда q в этом поле:.

Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим,

где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r  ), тогда постоянная C = 0 и предыдущее выражение принимает вид

.При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:.

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением,

где rij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

5) Для установления связи между силовой характеристикой электрического поля  напряжённостью и его энергетической характеристикой  потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA =  dWп =  q d, где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl  d или в декартовой системе координат Ex dx + Ey dy + Ez dz = d,      (1.8)

где Ex, Ey, Ez - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда .

Стоящее в скобках выражение является градиентом потенциала , т. е.E =  grad = .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 40r. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

.Проекция же градиента потенциала на направление вектора , перпендикулярного вектору r, равна , т. е. в этом направлении потенциал электрического поля является постоянной величиной (  const). В рассмотренном случае направление вектора r совпадает с направлением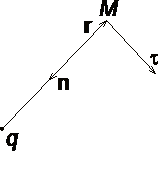рис. 1.6 силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

рис. 1.7

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали  штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.

6) Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.

Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга

Произведение вектора проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов называется дипольным моментом

Во внешнем электрическом поле на электрический диполь действует момент сил который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.

Потенциальная энергия электрического диполя в электрическом поле равна

Вдали от электрического диполя напряжённость его электрического поля убывает с расстоянием как R − 3, то есть быстрее, чем у точечного заряда (E˜R − 2).

Любая в целом электронейтральная система, содержащая электрические заряды, в некотором приближении может рассматриваться как электрический диполь с моментом где  — заряд i-го элемента,  — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.

Вычислим потенциал j поля в произвольной точке оси х. По принципу суперпозиции, он равен сумме потенциалов и  созданных положительным и отрицательным зарядами.                         Пусть х > 0, тогда: 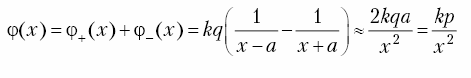                    (3) (выражение для (х) для х < 0 будет c другим знаком). 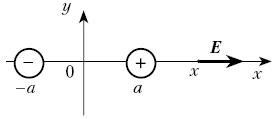Из симметрии задачи ясно, что на оси х вектор напряжённости поля E имеет только составляющую Ех. Её можно вычислить, исходя из известной формулы, связывающей напряжённость поля и потенциал: (4) но в школьном курсе формулу (4) обычно обходят стороной, поэтому вычислим Ех непосредственно: или Итак, при удалении от диполя по оси х или по оси y поле спадает как r–3. Можно доказать, что так же ведёт себя поле по любому направлению. Выражение для потенциала в произвольной точке приведём без вывода:   (т.е. при удалении по любому направлению, кроме оси Y, потенциал спадает как r–2). Убедитесь, что в частных случаях эта формула приводит к уже известным нам результатам.

55.Решение волнового уравнения. Плоская электромагнитная волна.

(2) Плоская электромагнитная волна - электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют одинаковые напряженности электрических или магнитных полей.

56.Опыты по получению электромагнитного излучения. Опыты Лебедева. Теория Максвелла не только предсказала существование электромагнитных волн, но и указала условия, необходимые для успеха опытов: достаточно высокая частота электрических колебаний и открытая форма цепи. Герц, предпринимая в 1888 г. свои известные опыты, постарался выполнить эти условия: он заменил колебательный контур прямолинейным вибратором. Для возбуждения электрических колебаний в то время был известен только один способ — искровой разряд. На рис. 122 изображена схема соответствующего устройства (вибратор Герца). Вибратор 1 имеет посередине разрыв 2 — искровой промежуток, к концам которого подводится напряжение от повышающего трансформатора. Указанная схема вполне аналогична схеме на рис. 51, рассмотренной в § 28, только вместо замкнутого контура с конденсатором и катушкой здесь применена открытая цепь, обеспечивающая хорошее излучение. Возбуждение же колебаний в этой цепи происходит совершенно так же, как описано в § 28, так что в вибраторе возникают регулярно повторяющиеся вспышки высокочастотных затухающих колебаний (рис. 52). Период этих колебаний и, следовательно, длина излучаемых электромагнитных волн задаются размерами вибратора (§ 56) Рис. 123. Приемные вибратор и виток для опытов Герца Для обнаружения волн Герц использовал второй вибратор с гораздо меньшей длиной искрового промежутка (доли миллиметра вместо 7,5 мм в излучающем вибраторе). Кроме такого приемного вибратора, применялся и Приемный виток, согнутый из проволоки в виде прямоугольника и тоже прерванный очень малым искровым промежутком (рис. 123). Под действием электромагнитной волны в этих приемниках возникают вынужденные колебания. Если приемники (вибратор или виток) настроены в резонанс на частоту излучателя, то при определенных условиях, которые мы рассмотрим дальше (§ 59), в их Искровых промежутках проскакивают очень маленькие и слабые искорки. Наблюдая появление или отсутствие таких искорок при различных условиях излучения и распространения волн, а также при различных расположениях приемников, можно было судить о свойствах наблюдаемых волн. О трудности этих опытов говорит, например, то, что искорки в приемниках большей частью можно было видеть только В темноте и неутомленным глазом. В своих опытах Герц осуществил получение электромагнитных волн и сумел воспроизвести с этими волнами все явления, типичные для любых волн: образование «тени» позади хорошо отражающих (металлических) предметов, Отражение от металлических листов, преломление в большой призме, сделанной из асфальта, образование стоячей волны в результате интерференции волны, падающей отвесно на металлический лист, со встречной волной, отраженной этим листом. Было исследовано также направление векторов Е и В электрического и магнитного полей б электромагнитных волнах; оказалось, что электромагнитные волны имеют такие же свойства, какие были известны у световых волн (поляризация, § 59). Таким образом, опыты Герца подвели прочную основу под теорию Максвелла: электромагнитные волны, предсказанные максвелловской теорией (§ 55), оказались реализованными на опыте. Выдающегося успеха в исследовании электромагнитных волн достиг русский физик Петр Николаевич Лебедев (1866—1912). В 1895 г. он получил с помощью вибраторов миллиметровых размеров волны длиной 6 мм, которые, как сам он писал, «...были ближе к более длинным волнам теплового спектра, чем к электрическим волнам, которыми вначале пользовался Герц...». Вся аппаратура, собственноручно сделанная Лебедевым для этих опытов, в особенности приемный вибратор, состоящий из двух кусочков проволоки длиной 3 мм с микроскопическим термоэлементом, впаянным между ними, представляет собой замечательный образец экспериментального искусства. Некоторые . оригинальные приборы Лебедева изображены на рис. 124.

59.Свойства световой волны. Явление дисперсии. Поляризация.

Поляризация.

Поляризация — для электромагнитных волн это явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H. Когерентное[источник не указан 328 дней] электромагнитное излучение может иметь:

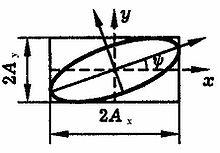
Эллипс поляризацииЛинейную поляризацию — в направлении, перпендикулярном направлению распространения волны; Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции; Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.

Некогерентное излучение может быть не поляризованным, либо быть полностью или частично поляризованным.При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. Тогда можно говорить о вертикальной и горизонтальной линейных поляризациях волны.