8. Задачи восстановления зависимостей [5]

При восстановлении функциональной зависимости могут быть выделены различные постановки задачи, которые сходятся к одной и той же математической схеме – минимизация среднеквадратичного риска по эмпирическим данным. Эти постановки различаются тем, в каком классе функций ведётся восстановление искомой зависимости: в классе индикаторных функций (в классе распознавания образов), в классе интегрируемых с квадратом функций (задача восстановления регрессии), в классе функций, являющихся образом некоторого другого класса функций (задача интерпретации результатов косвенного эксперимента).

8.1. Задача восстановления регрессии

Два множества связаны функциональной зависимостью, если х может быть поставлен в соответствие некоторый элемент у.

Если х определяет у однозначно, то это функция.

Если х определяет у через некоторую условную плотность P(y|x), то такая зависимость называется стохастической.

На практике часто достаточно знать функцию условного математического ожидания:

.

Функция у называется функцией регрессии или просто регрессией.

8.1.1. Постановка задачи

Пусть случайная величина х, характеризующаяся плотностью Р(х), имеет реализации х₁, …, х_l, и пусть имеется преобразование, которое каждому вектору х_i ставит в соответствие число у_i , полученное в результате реализации случайного испытания по закону P(y|x), и пусть свойства P(x) и P(y|x) нам неизвестны. Требуется по известной выборке x₁,…x_l; y₁, …, y_L восстановить регрессию, то есть в классе функций F(x, ) отыскать функцию F(x, ^*), наиболее близкую к регрессии y(x).

Если говорим о классе функции, значит мы себя ограничиваем этим классом (например классом линейных функций). Если этот класс не удовлетворяет нас по точности восстановления зависимости, то следует выбрать другой класс и найти новые значения коэффициентов ^*.

Эта задача обычно решается только при выполнении некоторых допущений:

1. Систематическая ошибка х равна нулю.

2. Случайные величины y(x_i) и y(x_j) при i  j независимы.

При выполнении этих условий задача сводится к минимизации следующего функционала:

(8.1)

на множестве ,

где – класс функций, интегрируемых с квадратом по мере P(x);

у(х) – уравнение регрессии.

В работе [5], используя зависимость , доказано, что (8.1) можно привести к виду

, если . (8.2)

Величина I() называется качеством функции (I() – дисперсия ошибки).

8.1.2. Восстановление регрессии функции одной переменной

Воспользуемся методом минимизации функционала (8.2), приведенном в работе [2]. Для этого рассмотрим гильбертово пространство L₂ действительных функций, интегрируемых с квадратом на отрезке [a, b]. Норма в L₂ задана следующим образом:

,

а скалярное произведение функций задано как

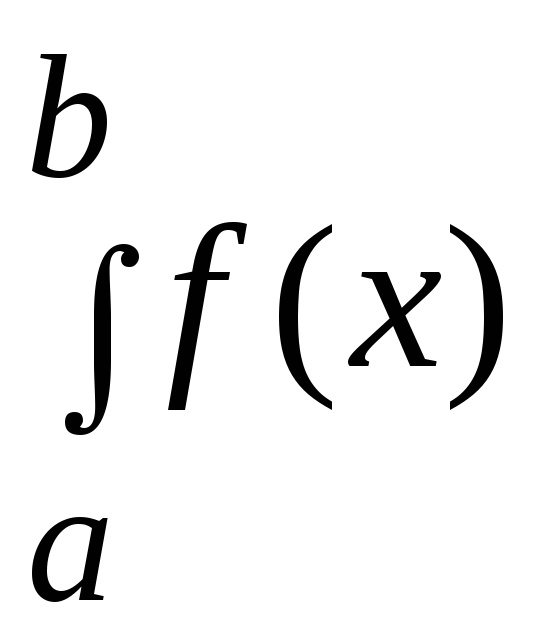
(f, ) = (x) dx. (8.3)

Регрессию будем искать в виде

 (x) =  _k(x), (8.4)

где  (x) – линейная функция от _k(x), в которой _k(x) линейно-независимы между собой.

Условие (8.2) в этих переменных может быть записано следующим образом:

|| y - 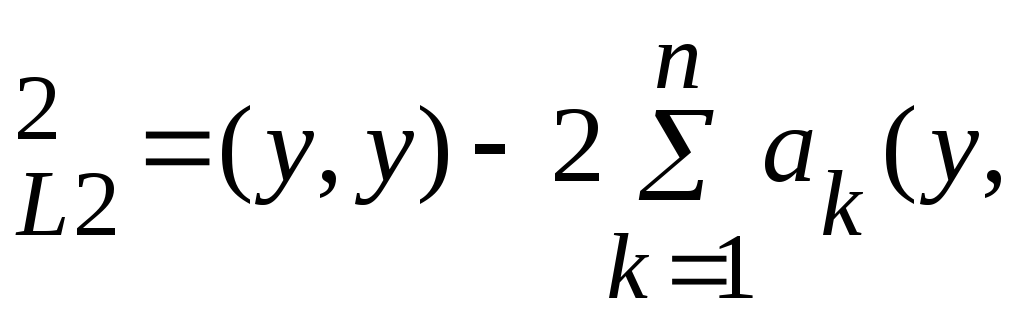 ||_k)(_k, _m). (8.5)

Сравним (8.2) и (8.5). Уравнение (8.2) определяет математическое ожидание от квадрата разности (y - )².

Уравнение (8.5) определяет интеграл от квадрата разности (y - )² на интервале [a, b], но согласно теореме Чебышева [6]

,

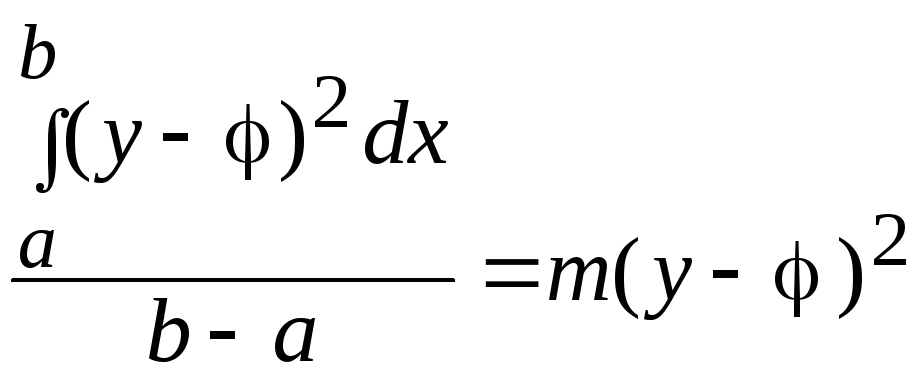уравнения (8.2) и (8.5) эквивалентны, так как при минимизации коэффициент (b - a) на положение минимума не влияет.

Найдем условие минимизации уравнения (8.5), приравнивая нулю производную по коэффициентам а_k. Получаем систему уравнений:

_k, _m) a_m = (y, _k), . (8.6)

Определитель этой системы есть определитель Грамма функции _k(x), так как функции _k линейно-независимы, то определитель отличен от нуля.

Для случая полиномиальной аппроксимации (х) = х^k уравнение (8.6) принимает вид

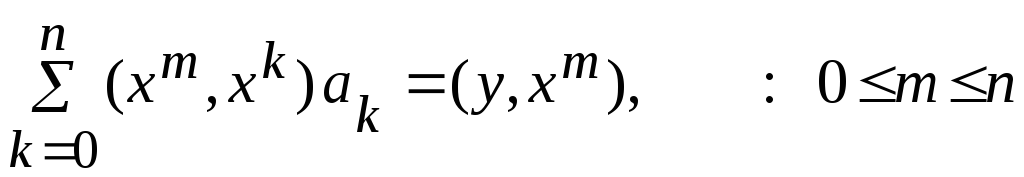, (8.7)

где ,

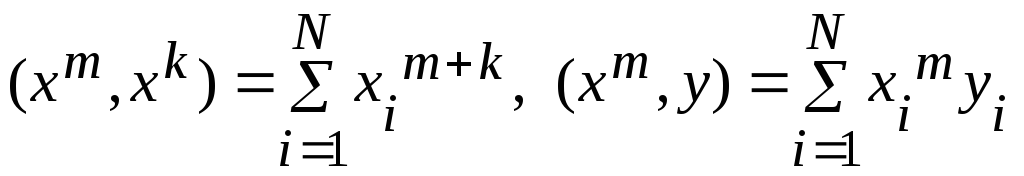N – размер статистики (нумерация экспериментов).

Система уравнений (8.7) является линейной относительно неизвестных коэффициентов , поэтому её легко решить каким-либо из известных методов (например, методом Гаусса).