
- •7.2. Моделирование непрерывных случайных величин
- •8. Задачи восстановления зависимостей [5]
- •8.1. Задача восстановления регрессии
- •8.1.1. Постановка задачи
- •8.1.2. Восстановление регрессии функции одной переменной
- •8.1.3 Восстановление регрессии функции нескольких переменных
- •8.1.4. Восстановление зависимости самообучающейся модели
- •9. Методы обучения распознаванию образов
- •9.1. Постановка задачи
- •9.2. Построение обобщенного портрета
- •9.3. Метод приближенного определения положения разделяющей плоскости
- •Нормаль
- •Нахождение векторов, образующих конус
- •9.4. Пример реализации
- •10. Основные принципы реализации иерархических моделей
7.2. Моделирование непрерывных случайных величин
Пусть непрерывная случайная величина, заданная интегральной функцией распределения.
![]() ,
,
где
![]()
плотность вероятности распределения
случайной величины .
плотность вероятности распределения
случайной величины .
Для получения непрерывной случайной величины c заданным законом распределения воспользуемся методом обратной функции
![]() (),
(),
полученной решением уравнения
![]() .
.
Преобразуем
равномерно распределенную на интервале
(0, 1) величину
в
с требуемой плотностью вероятности
![]() ,
имеющей интегральную функцию
,
имеющей интегральную функцию
![]() .
Поясним данный метод. Допустим, нам
задан закон распределения случайной
величины ,
изображенный на рис. 7.1. Вероятность
того, что реализация случайной величины
будет меньше y,
равна .
На рис. 7.2 изображена функция, об-
.
Поясним данный метод. Допустим, нам
задан закон распределения случайной
величины ,
изображенный на рис. 7.1. Вероятность
того, что реализация случайной величины
будет меньше y,
равна .
На рис. 7.2 изображена функция, об-






 y
y
 1
1
F
(y)



0 y 0 1
Рис. 7.1. График функции распре- Рис. 7.2. График функции


 деления
деления
![]() .
.
![]() ().
().
ратная
F().
Если случайная переменная
равномерно распределена на интервале
(0,1), то вероятность того, что реализация
функции
![]() ()
будет меньше y,
будет равна .
Таким образом, используя обратную
функцию и датчик случайных чисел,
равномерно распределённых на интервале
(0,1) , можно смоделировать случайный
процесс, распределённый по любому
закону.
()
будет меньше y,
будет равна .
Таким образом, используя обратную
функцию и датчик случайных чисел,
равномерно распределённых на интервале
(0,1) , можно смоделировать случайный
процесс, распределённый по любому
закону.
Моделирование случайной величины , распределённой по нормальному закону распределения, осуществляется следующим образом. Задаются параметры случайного процесса: m математическое ожидание и среднеквадратичное ожидание, тогда плотность вероятности запишется следующим образом:
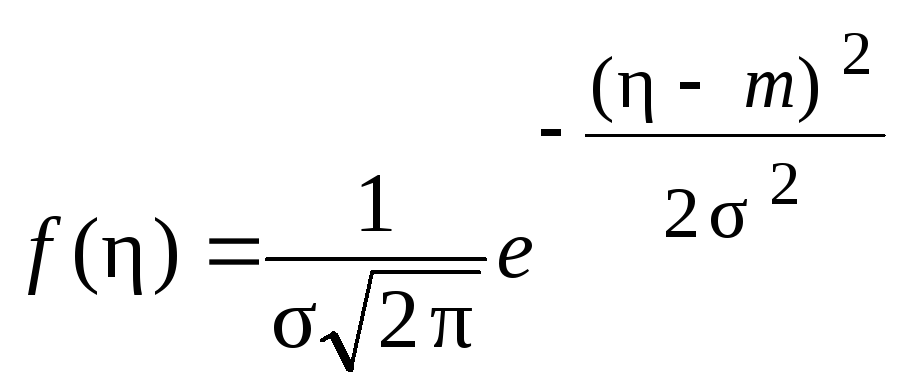 .
(7.1)
.
(7.1)
Для
определения интегральной функции F()
численно проинтегрируем уравнение
(7.1) , но плотность вероятности задана в
интервале
![]() ,
поэтому для практической реализации
этой задачи диапазон должен быть
сокращён. Воспользуемся для этого
неравенством Чебышева.
,
поэтому для практической реализации
этой задачи диапазон должен быть
сокращён. Воспользуемся для этого
неравенством Чебышева.
P(|X
- mx|
> n x)
<
![]() ,
(7.2)
,
(7.2)
где n число, определяющее диапазон значений случайной переменной x в частях среднеквадратичного отклонения.
Если мы хотим получить модель случайного процесса с точностью 4%, то n следует выбрать равным пяти. Тогда пределы интегрирования следует задавать m 5, m + 5. При интегрировании функции f() начальное значение F(m 5) следует принять равным 0,02 (2%), так как функция f() симметрична относительно математического ожидания.
Получить функцию F-1() можно, воспользовавшись методом интерполяции сплайнами. Для этого функцию F() задают таблично в диапазоне [m 5, m + 5] и по значениям этой таблицы методом интерполяции строят функцию F-1(.). Если в качестве аргумента этой функции использовать значения, полученные от генератора случайных чисел, то мы получим модель случайного процесса с заданными значениями m и .
