
- •Что называют электрическим током?
- •Зависимость сопротивления от температуры
- •Вольтамперная характеристика разряда
- •Электрический Ток в Вакууме
- •Электронно-дырочный переход
- •История открытия
- •Электромагнитная теория света
- •Вихревое электрическое поле
- •Классификация
- •Характеристики
- •Свойства электромагнитной волны.
- •Свойства электромагнитных волн
- •Закон Ома для переменного тока
- •3.6. Развитие представлений о природе света
- •Законы теплового излучения.
- •Законы внешнего фотоэффекта
- •Химическое действие света
Электронно-дырочный переход
При непосредственном соединении п-полупроводника с р-полупроводником в месте контакта (границы) этих полупроводников сформируется п – р-переход или электронно-дырочный.
Объясняется это способностью электронов из п-полупроводника переходить в р-полупроводник. Как следствие уменьшается число электронов и образовывается область с положительным зарядом в п-полупроводнике недалеко от пограничной области с р-полупроводником. В свою очередь также перемещаются и дырки, что становится ещё большим усилителем избыточности положительного заряда на границе п-полупроводника. Таким образом в месте пересечения двух полупроводников, которые обладают различной проводимостью, формируется разность потенциалов, препятствующая последующим переходам электронов и перемещению дырок. Вследствие этого пограничный слой называется запирающим слоем.
Существенным изменениям под воздействием внешнего электрического поля подвергается сопротивление запирающего слоя.
Например: если положительный полюс источника тока соединить с р-полупроводником, а отрицательный – с п-полупроводником, то под воздействием электрического поля, которое создаётся этим источником тока, электроны и дырки, являющиеся носителями зарядов, не встречая заметного сопротивления, перейдут через запирающий слой. Электрический ток, который образующийся в результате такого процесса называют прямым током, его сила при этом может быть значительной.
И, наоборот, при соединении положительного полюса источника тока с п-полупроводником, а отрицательного – с р-полупроводником, сопротивление запирающего слоя проходя через него будет довольно большим. В таком случае электронно-дырочный переход заперт. Тем не менее, реальные полупроводники всегда обладают небольшим количеством электронов проводимости, которые и создадут электрический ток в рассматриваемом случае. Такой ток называется обратным, его сила незначительна.
На основании изложенного несложно понять: полупроводник с электронно-дырочным переходом – обладатель вентильного свойства. То есть ток через п – р-переход имеет способность проходить только в одном направлении. Основа применения полупроводников для выпрямления переменного тока заключается именно на данном явлении.
21.открытие магнитного поля
История открытия
До начала XIX в. электричество и магнетизм считались явлениями, не связанными друг с другом, и рассматривались в разных разделах физики.
В 1819 г. датский физик Г. Х. Эрстед обнаружил, что проводник, по которому течёт электрический ток, вызывает отклонение стрелки магнитного компаса, из чего следовало, что электрические и магнитные явления взаимосвязаны.
Французский физик и математик А. Ампер в 1824 г. дал математическое описание взаимодействия проводника тока с магнитным полем (см. Закон Ампера).
В 1831 г. английский физик М. Фарадей экспериментально обнаружил и дал математическое описание явления электромагнитной индукции — возникновения электродвижущей силы в проводнике, находящемся под действием изменяющегося магнитного поля.
В 1864 г. Дж. Максвелл создаёт теорию электромагнитного поля, согласно которой электрическое и магнитное поля существуют как взаимосвязанные составляющие единого целого — электромагнитного поля. Эта теория с единой точки зрения объясняла результаты всех предшествующих исследований в области электродинамики, и, кроме того, из неё вытекало, что любые изменения электромагнитного поля должны порождать электромагнитные волны, распространяющиеся в диэлектрической среде (в том числе в пустоте) с конечной скоростью, зависящей от диэлектрической и магнитной проницаемости этой среды. Для вакуума теоретическое значение этой скорости было близко к экспериментальным измерениям скорости света, полученным на тот момент, что позволило Максвеллу высказать предположение (впоследствии подтвердившееся), что свет является одним из проявлений электромагнитных волн.
Теория Максвелла уже при своем возникновении разрешила ряд принципиальных проблем электромагнитной теории, предсказав новые эффекты и дав надежную и эффективную математическую основу описанию электромагнитных явлений. Однако при жизни Максвелла наиболее яркое предсказание его теории — предсказание существования электромагнитных волн — не получило прямых экспериментальных подтверждений.
В 1887 г. немецкий физик Г. Герц поставил эксперимент, полностью подтвердивший теоретические выводы Максвелла. Его экспериментальная установка состояла из находящихся на некотором расстоянии друг от друга передатчика и приёмника электромагнитных волн, и фактически представляла собой исторически первую систему радиосвязи, хотя сам Герц не видел никакого практического применения своего открытия, и рассматривал его исключительно как экспериментальное подтверждение теории Максвелла.
В XX в. развитие представлений об электромагнитном поле и электромагнитном излучении продолжилось в рамках квантовой теории поля, основы которой были заложены великим немецким физиком Максом Планком. Эта теория, в целом завершенная рядом физиков около середины XX века, оказалась одной из наиболее точных физических теорий, существующих на сегодняшний день.
Во второй половине XX века (квантовая) теория электромагнитного поля и его взаимодействия была включена в единую теорию электрослабого взаимодействия и ныне входит в так называемую стандартную модель в рамках концепциикалибровочных полей (электромагнитное поле является с этой точки зрения простейшим из калибровочных полей — абелевым калибровочным полем).
22.силовые линии магнитного поля
Силовые линии
линии, проведённые в каком-либо силовом поле (электрическом, магнитном, гравитационном), касательные к которым в каждой точке пространства совпадают по направлению с вектором, характеризующим данное поле (напряжённостью электрического или гравитационного полей, магнитной индукцией). Изображение силовых полей с помощью С. л. — частный случай изображения любых векторных полей (См. Векторное поле) с помощью линий тока (См. Линии тока). Т. к. напряжённости полей и магнитная индукция — однозначные функции точки, то через каждую точку пространства может проходить только одна С. л. Густота С. л. обычно выбирается так, чтобы через единичную площадку, перпендикулярную к С. л., проходило число С. л., пропорциональное напряжённости поля (или магнитной индукции) на этой площадке. Т. о., С. л. дают наглядную картину распределения поля в пространстве: густота С. л. и их направление характеризуют величину и направление напряжённости поля. С. л. электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). С. л. вектора магнитной индукции всегда замкнуты, т. е. магнитное поле является вихревым. Железные опилки, помещенные в магнитное поле, выстраиваются вдоль С. л.; благодаря этому можно экспериментально определять вид С. л. магнитной индукции. Вихревое электрическое поле, порождаемое изменяющимся магнитным полем, также имеет замкнутые С. л.
23.магнитные поля прямолинейного проводника с током, кругового тока и соленоида
24.взаимодействие параллельных токов
Как
нам уже известно, магнитное поле оказывает
на рамку с током ориентирующее действие.
Значит, вращающий момент, который
испытывает рамка, является результатом
действия сил на отдельные ее элементы.
Сравнивая и обобщая результаты
исследования действия магнитного поля
на различные проводники с током, Ампер
открыл, что сила dF,
с которой магнитное поле действует на
элемент проводника dl с
током, который находится в магнитном
поле, равна
![]() (1)
где
dl -
вектор, по модулю равный dl и
совпадающий по направлению с током, В -
вектор магнитной индукции.
Направление
вектора dF может
быть определено, используя (1), по правилу
векторного произведения, откуда
следует правило
левой руки:
если ладонь левой руки расположить так,
чтобы в нее входил вектор В,
а четыре вытянутых пальца расположить
по направлению тока в проводнике, то
отогнутый большой палец покажет
направление силы, которая действуюет
на ток.
Модуль
силы Ампера (см. (1)) равен
(1)
где
dl -
вектор, по модулю равный dl и
совпадающий по направлению с током, В -
вектор магнитной индукции.
Направление
вектора dF может
быть определено, используя (1), по правилу
векторного произведения, откуда
следует правило
левой руки:
если ладонь левой руки расположить так,
чтобы в нее входил вектор В,
а четыре вытянутых пальца расположить
по направлению тока в проводнике, то
отогнутый большой палец покажет
направление силы, которая действуюет
на ток.
Модуль
силы Ампера (см. (1)) равен
![]() (2)
где
α — угол между векторами dl и В.
Закон
Ампера используется при нахождении
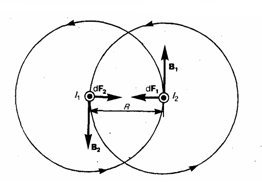
силы взаимодействия двух токов. Рассмотрим
два бесконечных прямолинейных параллельных
тока I1 и
I2;
(направления токов даны на рис. 1),
расстояние между которыми R. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на соседний проводник с током. Найдем,
с какой силой действует магнитное поле
тока I1 на
элемент dl второго
проводника с током I2.
Магнитное поле тока I1 есть
линии магнитной индукции, представляющие
собой концентрические окружности.
Направление вектора B1 задается
правилом правого винта, его модуль по
формуле (5) есть
(2)
где
α — угол между векторами dl и В.
Закон
Ампера используется при нахождении
силы взаимодействия двух токов. Рассмотрим
два бесконечных прямолинейных параллельных
тока I1 и
I2;
(направления токов даны на рис. 1),
расстояние между которыми R. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на соседний проводник с током. Найдем,
с какой силой действует магнитное поле
тока I1 на
элемент dl второго
проводника с током I2.
Магнитное поле тока I1 есть
линии магнитной индукции, представляющие
собой концентрические окружности.
Направление вектора B1 задается
правилом правого винта, его модуль по
формуле (5) есть
![]() Направление
силы dF1,
с которой поле B1 действует
на участок dl второго
тока, находится по правилу левой руки
и указано на рисунке. Модуль силы,
используя (2), с учетом того, что угол α
между элементами тока I2 и
вектором B1 прямой,
будет равен
Направление
силы dF1,
с которой поле B1 действует
на участок dl второго
тока, находится по правилу левой руки
и указано на рисунке. Модуль силы,
используя (2), с учетом того, что угол α
между элементами тока I2 и
вектором B1 прямой,
будет равен
![]() подставляя
значение для В1,
найдем
подставляя
значение для В1,
найдем
![]() (3)
Аналогично
рассуждая, можно показать, что сила
dF2 с
которой магнитное поле тока I2 действует
на элемент dl первого
проводника с током I1,
направлена в противоположную сторону
и по модулю равна
(3)
Аналогично
рассуждая, можно показать, что сила
dF2 с
которой магнитное поле тока I2 действует
на элемент dl первого
проводника с током I1,
направлена в противоположную сторону
и по модулю равна
![]() (4)
Сопоставление
выражений (3) и (4) дает, что
(4)
Сопоставление
выражений (3) и (4) дает, что
![]() т.
е. два
параллельных тока одинакового направления
притягиваются друг к другу с
силой, равной
т.
е. два
параллельных тока одинакового направления
притягиваются друг к другу с
силой, равной
![]() (5)
Если токи
имеют противоположные направления,
то, используя правило левой руки,
определим, что между
ними действует сила отталкивания,
определяемая выражением (5).
(5)
Если токи
имеют противоположные направления,
то, используя правило левой руки,
определим, что между
ними действует сила отталкивания,
определяемая выражением (5).
25.действие магнитного поля на проводник с током
ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ПРОВОДНИК С ТОКОМ
Магнитное поле действует с некоторой силой на любой проводник с током, находящийся в нем. Если проводник, по которому протекает электрический ток подвесить в магнитном поле, например, между полюсами магнита, то магнитное поле будет действовать на проводник с некоторой силой и отклонять его.
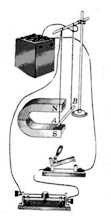
Направление движения проводника зависит от направления тока в проводнике и от расположения полюсов магнита.
26.магнитный поток.Работа при перемещении проводника с током в магнитном поле
МАГНИТНЫЙ ПОТОК (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m - магнитная ПРОНИЦАЕМОСТЬ среды, а Н - интенсивность магнитного поля. Плотность магнитного потока - это поток на единицу площади (символ В), который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим
прямоугольный контур с током 1-2-3-4-1 (рис.
2.18). Магнитное поле направлено от нас
перпендикулярно плоскости контура.
Магнитный поток ![]() ,
пронизывающий контур, направлен по
нормали
,
пронизывающий контур, направлен по
нормали ![]() к
контуру, поэтому
к
контуру, поэтому ![]() .
.
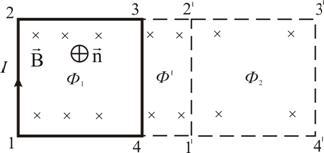
Рис. 2.18
Переместим
этот контур параллельно самому себе в
новое положение 1'-2'-3'-4'-1'. Магнитное поле
в общем случае может быть неоднородным
и новый контур будет пронизан
магнитным потоком ![]() .
.
Площадка
4-3-2'-1'-4, расположенная между старым и
новым контуром, пронизывается потоком ![]() .
.
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
![]()
где ![]() ,
, ![]() равны
нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку).
равны
нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку).
![]() .
.
Провод
1–2 перерезает поток ( ![]() ),
но движется против сил действия магнитного
поля.
),
но движется против сил действия магнитного
поля.
![]() .
.
Тогда общая работа по перемещению контура
![]() или
или
|
|
|
(2.9.2) |
|
здесь ![]() –
это изменение
магнитного потока, сцепленного с
контуром.
–
это изменение
магнитного потока, сцепленного с
контуром.
Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.
Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
|
|
|
(2.9.5) |
|
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен.
Соотношение
(2.9.5), выведенное нами для простейшего
случая, остаётся справедливым для
контура любой формы в произвольном
магнитном поле. Более того, если контур
неподвижен, а меняется ![]() ,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу
,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу ![]()
27.действие магнитного поля на движущийся заряд.Сила лоренца
ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД
Сила Лоренца
- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
![]()
где q - заряд частицы; V - скорость заряда; B - индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.
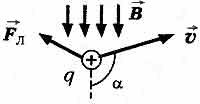
Направление силы Лоренца определяется по правилу левой руки:
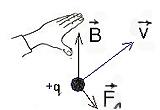
Если
поставить левую руку так, чтобы
перпендикулярная скорости составляющая
вектора индукции входила в ладонь, а
четыре пальца были бы расположены по
направлению скорости движения
положительного заряда (или против
направления скорости отрицательного
заряда), то отогнутый большой палец
укажет направление силы Лоренца
. 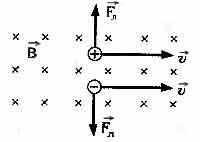
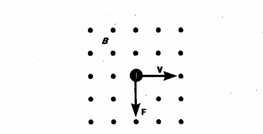
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно. Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной
![]() и
создает центростремительное ускорение
равное
и
создает центростремительное ускорение
равное
![]()
В этом случае частица движется по окружности.
.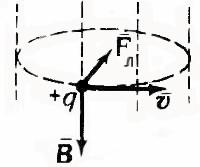 Согласно
второму закону Ньютона: сила Лоренца
равнв произведению массы частицы на
центростремительное ускорение
Согласно
второму закону Ньютона: сила Лоренца
равнв произведению массы частицы на
центростремительное ускорение
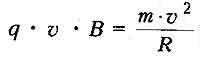 тогда радиус
окружности
тогда радиус
окружности
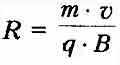 а период
обращения заряда в
магнитном поле
а период
обращения заряда в
магнитном поле
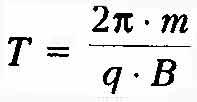
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные
28.движение заряженной частицы в магнитном поле
Формула
силы Лоренца дает возможность найти
ряд закономерностей движения заряженных
частиц в магнитном поле. Зная направление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле можно найти знак заряда
частиц, которые движутся в магнитных
полях.
Для
вывода общих закономерностей будем
полагать, что магнитное поле однородно
и на частицы не действуют электрические
поля. Если заряженная частица в магнитном
поле движется со скоростью v вдоль
линий магнитной индукции, то угол α
между векторами v и Вравен
0 или π. Тогда сила Лоренца равна нулю,
т. е. магнитное поле на частицу не
действует и она движется равномерно и
прямолинейно.
В
случае, если заряженная частица движется
в магнитном поле со скоростью v,
которая перпендикулярна вектору В,
то сила ЛоренцаF=Q[vB]
постоянна по модулю и перпендикулярна
к траектории частицы. По второму закону
Ньютона, сила Лоренца создает
центростремительное ускорение. Значит,
что частица будет двигаться по окружности,
радиус r которой находится из условия
QvB=mv2/r
, следовательно
![]() (1)
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
(1)
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
![]() Подствавив
(1), получим
Подствавив
(1), получим
![]() (2)
т.
е. период вращения частицы в однородном
магнитном поле задается только величиной,
которая обратна удельному заряду (Q/m)
частицы, и магнитной индукцией поля, но
при этом не зависит от ее скорости (при
v<<c). На этом соображении основано
действие циклических ускорителей
заряженных частиц.
В
случае, если скорость v заряженной
частицы направлена под углом α к
вектору В (рис.
170), то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v подставить
vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
(2)
т.
е. период вращения частицы в однородном
магнитном поле задается только величиной,
которая обратна удельному заряду (Q/m)
частицы, и магнитной индукцией поля, но
при этом не зависит от ее скорости (при
v<<c). На этом соображении основано
действие циклических ускорителей
заряженных частиц.
В
случае, если скорость v заряженной
частицы направлена под углом α к
вектору В (рис.
170), то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v подставить
vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
![]() Подставив
в данное выражение (2), найдем
Подставив
в данное выражение (2), найдем
![]() Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если
скорость v заряженной
частицы составляет угол α с направлением
вектора В неоднородного
магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличением В.
На этом основана фокусировка заряженных
частиц в магнитном поле.
Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если
скорость v заряженной
частицы составляет угол α с направлением
вектора В неоднородного
магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличением В.
На этом основана фокусировка заряженных
частиц в магнитном поле.
29.опыты Фарадея.Электромагнитная индукция
Опыт?1 Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонения стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изменится. Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид. Опыт?2 Концы одной из катушек, вставленных одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблюдается в моменты включения или выключения тока, в моменты его увеличения или уменьшения или при перемещении катушек относительно друг друга. Направления отклонений стрелки гальванометра также противоположны при включении и выключении тока, его увеличении и уменьшении, сближении и удалении катушек. Выводы: 1. индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции. 2. сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения. Обобщая результаты опытов, Фарадей показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы электромагнитной индукции. Правило Ленца: Индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток. При приближении магнита к замкнутому проводнику ΔФ/Δt>0. Вi ? магнитная индукция поля индукционного тока Ii, прич?м направления Вi и индукционного тока подчиняются правилу правого винта. Закон Фарадея: ЭДС εi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: εi=-ΔФ/Δt. Единица ? вольт. Этот закон является универсальным: ЭДС не зависит от способа изменения магнитного потока. Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Вихревое электрическое поле ? электрическое поле, порождаемое переменным магнитным полем. Силовые линии вихревого электрического поля всегда замкнуты. В отличие от электростатического поля работа вихревого электрического поля на замкнутом пути не равна 0. Работа вихревого электрического поля по перемещению единичного ?+? заряда вдоль замкнутого неподвижного проводника равна ЭДС индукции в этом проводнике. εi=BVLsinA. Самоиндукция ? возникновение ЭДС индукции в проводящем контуре при изменении в н?м силы тока. Взаимная индукция ? возникновение ЭДС в одном их контуров при изменении силы тока в другом.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем в 1831 году. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
30.закон электромагнитной индукции.Правило Ленца
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ, закон Фарадея – закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Пусть в однородном магнитном поле В помещен прямолинейный отрезок проводника. При передвижении его перпендикулярно силовым линиям (рис.1) заряды под действием магнитной силы начнут передвигаться вдоль проводника перпендикулярно к направлению и к вектору поля В. Направление тока легко установить по правилу правой руки. Ток будет течь до тех пор, пока на концах проводника не образуются заряды противоположного знака, которые создадут электрическое поле Е, направленное против силы, действующей на заряд. Электрические и магнитные силы уравновесят друг друга, и движение зарядов прекратится. Заряды накапливаются на концах проводника. Если поместить в магнитное поле замкнутый контур и двигать его так, чтобы плоскость рамки была перпендикулярна линиям однородного магнитного поля В, то ток потечет по стороне ab от a к b, и по dc от d к c (рис.2). Две другие стороны можно не рассматривать, так как сила, действующая на заряды, расположенные в проводнике, перпендикулярна к проводу, и движение зарядов прекращается. Если токи в сторонах ab и dc текут навстречу друг другу, что приводит к накоплению заряда, замкнутый ток по рамке не пойдет. Величина ЭДС вдоль рамки равна нулю (E + 0 – E + 0) Δ l = 0.
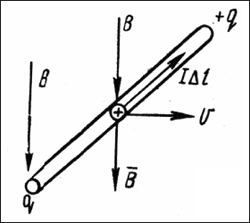
Рисунок 1.
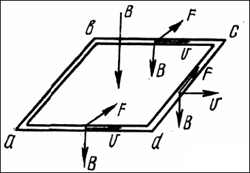
Рисунок 2.
При движении рамки в том же направлении dc выйдет из области, занимаемой магнитным полем, и поток магнитного поля через плоскость рамки начнет уменьшаться. В этом случае сила, действовавшая на заряды, принадлежащие стороне dc, исчезнет, и заряды, движущиеся от a к b, ничто уравновешивать не будет. По рамке пойдет замкнутый ток. То же самое будет наблюдаться при движении, например, соленоида относительно неподвижно лежащей рамки.
Наведенная в проводе ЭДС электромагнитной индукции пропорциональна величине магнитной индукции поля, в котором движется проводник, длине провода и скорости его движения в направлении, перпендикулярном к магнитным силовым линиям.
При изменении магнитного потока через контур начинает идти ток (индукционный или наведенный), который обязан своим возникновением электрическому полю. Величина ЭДС поля зависит от скорости изменения магнитного потока.
Правило Ленца, правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток. Сформулировано в 1833 г. Э. Х. Ленцем.
Если ток увеличивается, то и магнитный поток увеличивается.
Если ![]() индукционный
ток направлен против основного тока.
индукционный
ток направлен против основного тока.
Если ![]() индукционный
ток направлен в том же направлении, что
и основной ток.
индукционный
ток направлен в том же направлении, что
и основной ток.
Индукционный ток всегда направлен так, чтобы уменьшить действие причины его вызывающей.
В обобщенной формулировке правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его первопричине.
31.понятие об электромагнитной теории максвелла
