
- •2. Структура регістра eflags
- •3. Організація оперативної пам’яті. Сегментована модель оперативної пам’яті. Формування адреси в реальному режимі
- •4. Формати і типи даних. Формат машинних команд. Система переривань
- •5. Десяткова арифметика. Форми зображення десяткових чисел
- •7. Ділення ascii-чисел.
- •6. Директиви сегментації. Директиви proc і endp
- •7. Опис простих типів мовою асемблера
- •10. Синтаксис команд мовою асемблера
- •11. Команди передач даних
- •Xchg ax, data1; (data2) в data1, (ax) – початковий стан
- •12. Стекові передачі даних
- •13. Передачі адресних об’єктів, команди введення-виведення і передачі прапорців
- •14. Команди передачі даних movXx. Команда setCc. Команда xlat
- •15. Команди додавання, віднімання і порівняння
- •Inc reg/mem; Розмір 8/16/32.
- •16. Команди множення і ділення
- •20. Команди логічних операцій. Команди зсувів
- •22. Команди операцій з двійковими ланцюжками
- •23. Команди передачі керування (безумовні переходи)
- •24. Команди умовних переходів і команди керування циклами
- •26. Команди переривань і повернення з переривань
- •Загальні поняття.
- •Використання префіксів в ланцюжкових командах.
- •Команда movs.
- •Команда cmps.
- •Команда scas.
- •Команда lods.
- •Команда stos.
- •Команди введення/виведення ланцюжків.
- •29. Команди керування процесором
- •Команди, які впливають на прапорці.
- •Команди синхронізації.
- •Системні команди
- •31. Формати даних, які підтримуються fpu
- •Параметри для трьох форматів в таблиці
- •32. Програмна модель fpu
- •33. Слово стану sw і слово керування cw пристрою fpu.
- •Відповідність між кодом умови і прапорцями
- •34. Команди передач даних fpu: завантаження, збереження, збереження з вибором зі стека, обміну, завантаження сталих.
- •35. Арифметичні команди fpu: додавання, віднімання, множення, ділення.
- •36. Додаткові арифметичні команди fpu.
- •37. Команди порівняння fpu
- •38. Команди трансцендентних функцій. Алгоритми обчислення значень функцій і та логарифмів за будь-якою основою.
- •39. Команди керування пристроєм fpu
- •40. Спеціальні числові значення та особливі обчислювальні ситуації
38. Команди трансцендентних функцій. Алгоритми обчислення значень функцій і та логарифмів за будь-якою основою.
Команда
 – обчислення часткового тангенса. Вона
сприймає в
– обчислення часткового тангенса. Вона
сприймає в
 число з діапазону від
число з діапазону від
 до
до
 ,
яке вважається аргументом в радіанах.
Повертає результат у двох верхніх
регістрах стека: значення тангенса
заданого кута
,
яке вважається аргументом в радіанах.
Повертає результат у двох верхніх
регістрах стека: значення тангенса
заданого кута
 заміщує аргумент і в стек записується
1.0. Такі дії пояснюються сумісністю зі
співпроцесорами 8087 і 80287, в яких команда
заміщує аргумент і в стек записується
1.0. Такі дії пояснюються сумісністю зі
співпроцесорами 8087 і 80287, в яких команда
 дає тангенс, який дорівнює
дає тангенс, який дорівнює
 і значення в
і значення в
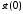 не дорівнює 1.0. Отже в цих співпроцесорах
для одержання тангенса потрібна ще одна
дія ділення (це й пояснює появу терміну
“частковий тангенс”). Крім того запис
у стек 1.0 спрощує обчислення інших
тригонометричних функцій. Наприклад,
котангенс можна обчислити, виконавши
після
не дорівнює 1.0. Отже в цих співпроцесорах
для одержання тангенса потрібна ще одна
дія ділення (це й пояснює появу терміну
“частковий тангенс”). Крім того запис
у стек 1.0 спрощує обчислення інших
тригонометричних функцій. Наприклад,
котангенс можна обчислити, виконавши
після
 команду
команду
 (
( ).
).
Якщо операнд не
припустимий, біт с2 коду умови установлюється
в 1 і
 залишається незмінним. Програмно
потрібно операнд звести до значення,
яке повинно знаходитися в діапазоні
від
залишається незмінним. Програмно
потрібно операнд звести до значення,
яке повинно знаходитися в діапазоні
від
 до
до
 ,
віднімаючи відповідне число, кратне
,
віднімаючи відповідне число, кратне
 .
Щоб не виникло особливого випадку
“недійсна операція”, регістр
.
Щоб не виникло особливого випадку
“недійсна операція”, регістр
 повинен бути порожнім.
повинен бути порожнім.
Команда
 – обчислення часткового арктангенса:
обчислює
– обчислення часткового арктангенса:
обчислює
 .
Після цього вилучення зі стека і кут
заміщує два операнди у вершині стека.
Результат має той же знак, що й операнд
в
.
Після цього вилучення зі стека і кут
заміщує два операнди у вершині стека.
Результат має той же знак, що й операнд
в
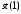 і величину
і величину
 .
Термін “частковий арктангенс”
успадкований від процесорів 8087 і 80287, в
яких були обмеження на значення в
.
Термін “частковий арктангенс”
успадкований від процесорів 8087 і 80287, в
яких були обмеження на значення в
 і
і
 .
У 80387 і FPU
обмежень на діапазон припустимих
аргументів команди
.
У 80387 і FPU
обмежень на діапазон припустимих
аргументів команди
 немає.
немає.
Те, що
 сприймає два аргументи і обчислює
сприймає два аргументи і обчислює
 їх відношення, спрощує обчислення інших
тригонометричних функцій. Наприклад,
їх відношення, спрощує обчислення інших
тригонометричних функцій. Наприклад,
 , (38.1)
, (38.1)
 . (38.2)
. (38.2)
Зрозуміло, що в
обох цих співвідношеннях
 .
.
Покажемо, що формули
(38.1) і (38.2) справджуються. Для доведення
формули (38.1) застосуємо до обох частин
цієї формули функцію
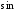


 .
.
Знайдемо
 .
Маємо
.
Маємо
 .
.
Оскільки
 ,
то одержуємо
,
то одержуємо
що
 .
Одержана рівність підтверджує правильність
співвідношення (38.1).
.
Одержана рівність підтверджує правильність
співвідношення (38.1).
Для доведення
(38.2) застосуємо до обох частин функцію




 .
.
Одержана рівність завершує доведення формули (38.2).
Для обчислення за формулою (38.1) потрібно виконати наступні кроки.
-
Якщо
 є мірою кута в градусах, то потрібно
виконати потрібні перетворення: число
градусів помножити на
є мірою кута в градусах, то потрібно
виконати потрібні перетворення: число
градусів помножити на
 ,
число мінут – на
,
число мінут – на
 ,
число секунд – на
,
число секунд – на
 і знайдені добутки додати.
і знайдені добутки додати. -
Записати
 в стек.
в стек. -
Обчислити значення виразу
 і записати його в стек.
і записати його в стек. -
Виконати команду
 (в
(в
 повинно бути значення виразу
повинно бути значення виразу
 ,
а в
,
а в
 –
–
 .
.
Як
результат цих дій в регістрі
 сформується значення виразу
сформується значення виразу
 .
Для виконання обчислень за формулою
(38.2) потрібно виконати дії:
.
Для виконання обчислень за формулою
(38.2) потрібно виконати дії:
-
Якщо
 є мірою кута в градусах, то потрібно
виконати потрібні перетворення: число
градусів помножити на
є мірою кута в градусах, то потрібно
виконати потрібні перетворення: число
градусів помножити на
 ,
число мінут – на
,
число мінут – на
 ,
число секунд – на
,
число секунд – на
 і знайдені добутки додати.
і знайдені добутки додати. -
Обчислити значення виразу
 і записати його в стек.
і записати його в стек. -
Обчислити значення виразу
 і записати його в стек.
і записати його в стек. -
Виконати команду
 (в
(в
 повинно бути значення виразу
повинно бути значення виразу
 ,
а в
,
а в
 –
–
 ).
).
Як
результат цих дій в регістрі
 сформується значення виразу
сформується значення виразу
 .
.
Виконуючи
команди
 і
і
 ,
процесор i486,
слідкує
за перериваннями.
Він може відмінити виконання цих команд
для обслуговування переривань. Обидві
команди дуже точні і виконуються швидко
(біля трьох разів повільніше, ніж команда
ділення).
,
процесор i486,
слідкує
за перериваннями.
Він може відмінити виконання цих команд
для обслуговування переривань. Обидві
команди дуже точні і виконуються швидко
(біля трьох разів повільніше, ніж команда
ділення).
Новими для 80387 і
FPU
є команди: обчислення синуса
 ,
косинуса –
,
косинуса –
 ,
а також синуса косинуса –
,
а також синуса косинуса –
 .
Для цих команд
.
Для цих команд
 - початковий кут в радіанах в діапазоні
– від
- початковий кут в радіанах в діапазоні
– від
 до
до
 .
Якщо кут за межами діапазону, команди
не виконуються, біт с2 установлюється
в 1 і
.
Якщо кут за межами діапазону, команди
не виконуються, біт с2 установлюється
в 1 і
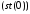 не змінюється.
Забезпечити допустимий діапазон для
початкового кута зобов’язаний програміст,
віднімаючи відповідне кратне
не змінюється.
Забезпечити допустимий діапазон для
початкового кута зобов’язаний програміст,
віднімаючи відповідне кратне
 .
.
Команди
 і
і
 повертають результат на місці аргументу,
а
повертають результат на місці аргументу,
а
 значення синуса на місці аргументу і
значення косинуса записується в стек.
значення синуса на місці аргументу і
значення косинуса записується в стек.
Команда
 використовується для обчислення виразу
використовується для обчислення виразу
 .
Значення
.
Значення
 береться з
береться з
 і повинно бути з діапазону
і повинно бути з діапазону
 .
Якщо операнд поза припустимим діапазоном,
результат невизначений. Віднімання 1
пов’язано з точністю обчислень, коли
значення
.
Якщо операнд поза припустимим діапазоном,
результат невизначений. Віднімання 1
пов’язано з точністю обчислень, коли
значення
 близьке до 0. Результат записується в
близьке до 0. Результат записується в
 замість операнда
замість операнда
 .
.
Якщо потрібно
обчислити значення виразу
 ,
то це можна зробити за формулою
,
то це можна зробити за формулою
 . (38.3)
. (38.3)
Вираз
 можна обчислити за допомогою команди
можна обчислити за допомогою команди
 ,
яка обчислює двійковий логарифм числа
,
яка обчислює двійковий логарифм числа
 і множить на
і множить на
 .
Аргумент
.
Аргумент
 повинен бути в регістрі
повинен бути в регістрі
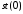 ,
а
,
а
 – в регістрі
– в регістрі
 ,
,
 – будь-яке додатне число, а
– будь-яке додатне число, а
 – будь-яке. Команда
– будь-яке. Команда
 обчислює логарифм числа з регістра
обчислює логарифм числа з регістра
 ,
множить його на
,
множить його на
 і повертає результат в
і повертає результат в
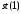 ,
,
 .
.
Якщо операнд в
 від’ємний, виникає особлива ситуація
“недійсна операція”.
від’ємний, виникає особлива ситуація
“недійсна операція”.
Отже, у виразі
(38.3) легко обчислити показник степеня,
тобто
 .
Якщо
.
Якщо
 ,
то далі легко обчислити
,
то далі легко обчислити
 ,
застосувавши команду
,
застосувавши команду
 .
Однак, якщо
.
Однак, якщо
 не з даного діапазону, потрібно виконати
додаткові обчислення за наступним
алгоритмом:
не з даного діапазону, потрібно виконати
додаткові обчислення за наступним
алгоритмом:
-
спочатку запишемо
 в
в
 ;
; -
застосуємо команду
 і одержимо в
і одержимо в
 мантису числа у форматі числа РТ з
характеристикою
мантису числа у форматі числа РТ з
характеристикою
 ,
а порядок числа в форматі числа РТ в
регістрі
,
а порядок числа в форматі числа РТ в
регістрі
 ;
; -
оскільки мантиса подана в нормалізованому вигляді, то вона за модулем більша або рівна 1. Тому для зведення мантиси до потрібного діапазону, якщо вона додатна, то від неї потрібно відняти 1 і до
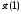 додати 1, а якщо вона від’ємна, то додати
1 і від
додати 1, а якщо вона від’ємна, то додати
1 і від
 відняти 1 (тепер
відняти 1 (тепер
 ,
де
,
де
 – вміст регістра
– вміст регістра
 ,
а
,
а
 ,
де
,
де
 – істинний порядок
– істинний порядок
 ;
; -
Застосуємо команду
 .
В
.
В
 одержимо
одержимо
 ;
; -
Виконаємо команду
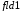 ;
; -
Виконаємо команду
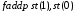 ,
в
,
в
 одержимо
одержимо
 ;
; -
Застосуємо тепер команду
 ,
в
,
в
 одержимо
одержимо
 .
.
Для обчислення логарифма за будь-якою основою можна використати формулу
 .
.
Команда
 – обчислює значення виразу:
– обчислює значення виразу:
 .
Значення
.
Значення
 вибирається з
вибирається з
 ,
причому
,
причому
 ,
значення
,
значення
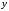 з регістра
з регістра
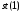 і може набувати будь-яких значень
і може набувати будь-яких значень
 .
Результат на місці
.
Результат на місці
 і
і
 .
Команда забезпечує більшу точність для
обчислення логарифмів чисел, близьких
до 1. Якщо
.
Команда забезпечує більшу точність для
обчислення логарифмів чисел, близьких
до 1. Якщо
 не з допустимого діапазону, то результат
команди
не з допустимого діапазону, то результат
команди
 невизначений. Команди
невизначений. Команди
 і
і
 можуть бути призупинені і відмінені в
зв’язку з обробкою переривання.
можуть бути призупинені і відмінені в
зв’язку з обробкою переривання.
