Параллелепипед

Теорема 4.8. 

Каждый параллелепипед имеет центр симметрии.

Следствие 4.1. 

Противоположные грани любого параллелепипеда равны и параллельны.

Определение 4.8. 

Прямоугольным называется параллелепипед, все грани которого прямоугольники.

Прямоугольный параллелепипед с равными ребрами называется кубом.

Три ребра, выходящие из одной вершины прямоугольного параллелепипеда называются его измерениями (длиной, шириной, высотой).

Теорема 4.9. 

Квадрат диагонали прямоугольного параллелепипеда равняется сумме квадратов его измерений: 

Заметим, что если ребро куба равно a, а его диагональ равна d, то  и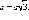 

Легко заметить, что все диагонали прямоугольного параллелепипеда равны.

Пирамида

Определение 4.9. 

Многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой.

Грани, отличные от основания, называются боковыми. Общая вершина боковых граней называется вершиной пирамиды.

Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания.

Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. В зависимости от числа сторон основания пирамида называется треугольной, четырехугольной, пятиугольной и т. д.

Определение 4.10. 

Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.

Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением.

Теорема 4.10. 

Если все боковые ребра пирамиды равны, то ее высота проходит через центр круга, описанного вокруг основания.

Теорема 4.11. 

Если все боковые грани пирамиды одинаково наклонены к плоскости основания, а высота проходит внутри пирамиды, то высота проходит через центр вписанного в основание пирамиды круга.

Теорема 4.12. 

Если все боковые грани наклонены к плоскости основания под одинаковым углом φ, то 

Эта формула справедлива, в частности, для правильной пирамиды.

Определение 4.11. 

Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.

Теорема 4.13. 

Для правильной пирамиды справедливы формулы:

•  где a – апофема боковой грани, P – периметр основания.

•  где n – число сторон основания, b – боковое ребро, α – плоский угол при вершине пирамиды.

Теорема 4.14. 

Если пирамиду пересечь плоскостью, параллельной плоскости основания, (чертеж 4.7.3), то:

Чертеж 4.7.3.

• боковые ребра и высота делятся этой плоскостью на пропорциональные отрезки в отношении 

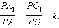
• площади сечения и основания пирамиды относятся как квадраты их расстояний до вершины пирамиды: