Параллельность прямых

Определение 2.1. 

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

Если две прямые a и b параллельны, то, как и в планиметрии, пишут a || b. В пространстве прямые могут быть размещены так, что они не пересекаются и не параллельны. Этот случай является особым для стереометрии.

Определение 2.2. 

Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.

Теорема 2.1. 

Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.

Замечание. Согласно определению, две параллельные прямые лежат в одной плоскости. Легко заметить, что через две параллельные прямые можно провести только одну плоскость.

Теорема 2.2. Признак скрещивающихся прямых.

Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещиваются.

Лемма 2.1. 

Если одна из двух параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.

Чертеж 2.1.3.

Теорема 2.3. Транзитивность параллельности.

Две прямые, параллельные третьей, параллельны между собой. Другими словами, если a || c и b || c, то a || b.

Параллельность прямой и плоскости

Определение 2.3. 

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Если прямая a параллельна плоскости α, то пишут a || α.

Теорема 2.4. Признак параллельности прямой и плоскости.

Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.

Теорема 2.5. Теорема о следе.

Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.

Определение 2.4. 

Прямую b иногда называют следом плоскости β на плоскости α.

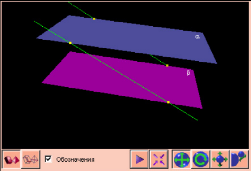
Параллельность двух плоскостей

Определение 2.5. 

Две плоскости называются параллельными, если они не имеют общих точек.

Теорема 2.6. Признак параллельности плоскостей.

Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.

Теорема 2.7. 

Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы.

Чертеж 2.3.2.

Теорема 2.8. 

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

Теорема 2.9. 

Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны.

Чертеж 2.3.3.

Теорема 2.10. 

Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.

Угол между двумя скрещивающимися прямыми

Определение 3.1. 

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

Определение 3.2. 

Две прямые в пространстве называются перпендикулярными, если они образуют прямой угол. На чертеже 3.1.2 изображен куб ABCDA₁B₁C₁D₁. Скрещивающиеся прямые A₁D₁ и CD перпендикулярны. Действительно, A₁D₁  C₁D₁, а C₁D₁ || CD.

Назовем еще несколько пар скрещивающихся перпендикулярных прямых: A₁D₁ и AB, A₁B₁ и BC, A₁B₁ и AD, B₁C₁ и AB.