Связь между векторами напряженности и индукции электрического поля

25) Если I = const то работа сил Ампера равна:

А=I*(Ф(1)-Ф(2))

где Ф(1) и Ф(2) - магнитные потоки сквозь контур в начальном и конечном положениях контура

Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.

Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле

,

26) Работа тока - работа электрического поля по переносу электрических зарядов вдоль проводника;

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.

Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:

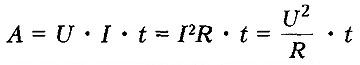
МОЩНОСТЬ ПОСТОЯННОГО ТОКА - отношение работы тока за время t к этому интервалу времени

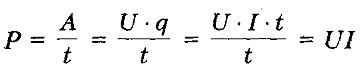
27) Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:

Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью каждая, расположенных на расстоянии друг от друга, в системе СИ выражается формулой:

Энергия W(е) конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

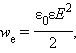
2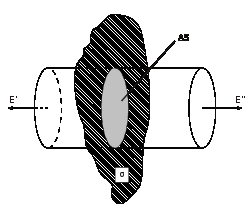8) Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим:

из которого

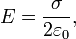
29) Постоянный ток — ток, направление и величина которого слабо меняется во времени.

Закон Ома: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна электрическому сопротивлению этого участка.

Закон Джоуля — Ленца: Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

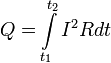
де dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления: