Задача нахождения кратчайшего пути

Постановка задачи:

Дан орграф G = (V, E), у которого все дуги имеют неотрицательные стоимости и вершина, определенная, как источник.

Задача состоит в нахождении стоимости кратчайших путей от источника ко всем другим вершинам графа G.

Длина пути определяется как сумма стоимостей дуг, составляющих путь.

Можно представить орграф G в виде карты маршрутов рейсовых полетов из одного города в другой, где каждая вершина соответствует городу, а дуга v–>w – рейсовому маршруту из города v в город w.

Метка этой дуги – это время перелета.

В этом случае решение задачи нахождения кратчайшего пути с одним источником для орграфа трактуется как минимальное время перелетов между различными городами.

Для решения поставленной задачи будем использовать «жадный» алгоритм, который часто называют алгоритмом Дейкстры. Алгоритм строит множество вершин S, для которых кратчайшие пути от источника уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от источника меньше, чем для других оставшихся вершин.

На каждом шаге алгоритма также используется массив D, в который записываются длины кратчайших путей для каждой вершины.

Когда множество S будет содержать все вершины орграфа, тогда массив D будет содержать длины кратчайших путей от источника к каждой вершине.

Пусть вершины в орграфе поименованы целыми числами, причем вершина 1 является источником.

Массив С – двумерный массив стоимостей, где элемент C[i][j] равен стоимости дуги ij. Если дуги не существует, то C[i][j] = .

Одномерный массив S, где S[i]=0, если вершина не принадлежит множеству S и 1 в противном случае.

void dijkstra(int n, int *s,

// n - число вершин графа

Int **c, // массив стоимостей

Int *d) // массив кратчайших

// путей

{

int i, j, min, k = 0;

s[0] = 1;

d[0] = 0;

for(i=1; i<n; i++)

// инициализация s и d

{

s[i] = 0;

d[i] = c[0][i];

}

for(i = 0; i < n; i++)

{

min = 32767;

for( j = 0; j < n; j++)

if(s[j]==0

&& d[j] < min)

{

min = d[j];

k = j;

}

s[k] = 1;

for(j = 0; j < n; j++)

if(s[j]==0)

d[j]= min(d[j],

d[k]+c[k][j]);

} // for i

} // djj

Пример.

Вначале S={1}, D[2]=10, D[3]=,

D[4]=30, D[5]=100.

На первом шаге цикла вершина 2 имеет минимальное значение в массиве D. Затем вычисляем D[3]=min(,10+50)=60. Остальные не изменяются так как нет дуг, исходящих из вершины 2 и ведущих к вершинам 4 и 5.

Остовные деревья минимальной стоимости

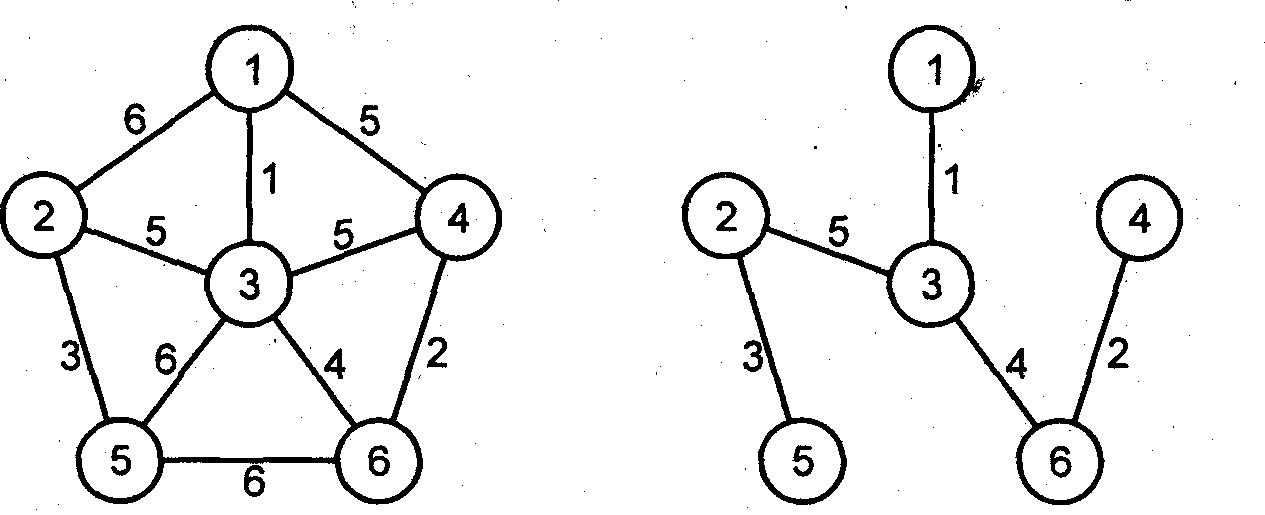
Пусть G = (V, Е) — связный граф, в котором каждое ребро (v, w) помечено числом с(v, w), которое называется стоимостью ребра.

Остовным деревом графа G называется свободное дерево, содержащее все вершины V графа G. Стоимость остовного дерева вычисляется как сумма стоимостей всех ребер, входящих в это дерево.

Неориентированный граф	Остовное дерево минимальной стоимости

Типичное применение остовных деревьев минимальной стоимости можно найти при разработке коммуникационных сетей. Здесь вершины графа представляют города, ребра – возможные коммуникационные линии между городами, а стоимость ребер соответствует стоимости коммуникационных линий. В этом случае остовное дерево минимальной стоимости представляет коммуникационную сеть, объединяющую все города коммуникационными линиями минимальной стоимости.

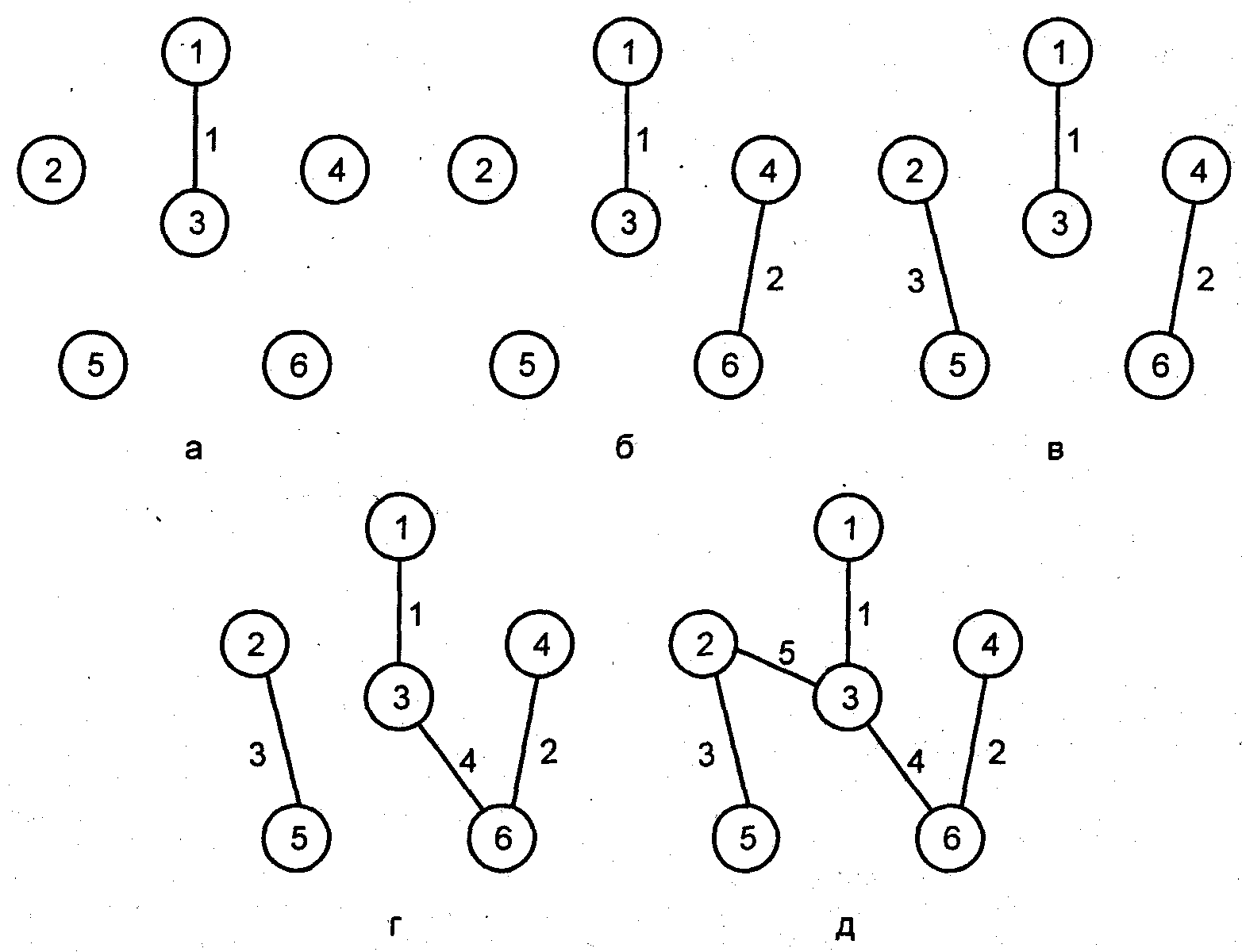
1. Построение остовного дерева минимальной стоимости (алгоритм Прима):

В этом алгоритме строится множество вершин U, из которого "вырастает" остовное дерево. Пусть V= {1, 2, ..., n}.

Сначала U = {1}. На каждом шаге алгоритма находится ребро наименьшей стоимости (u, v) такое, что u U и v V\U, затем вершина v переносится из множества V \ U в множество U. Этот процесс продолжается до тех пор, пока множество U не станет равным множеству V.

Последовательность построения остовного дерева приведена ниже.

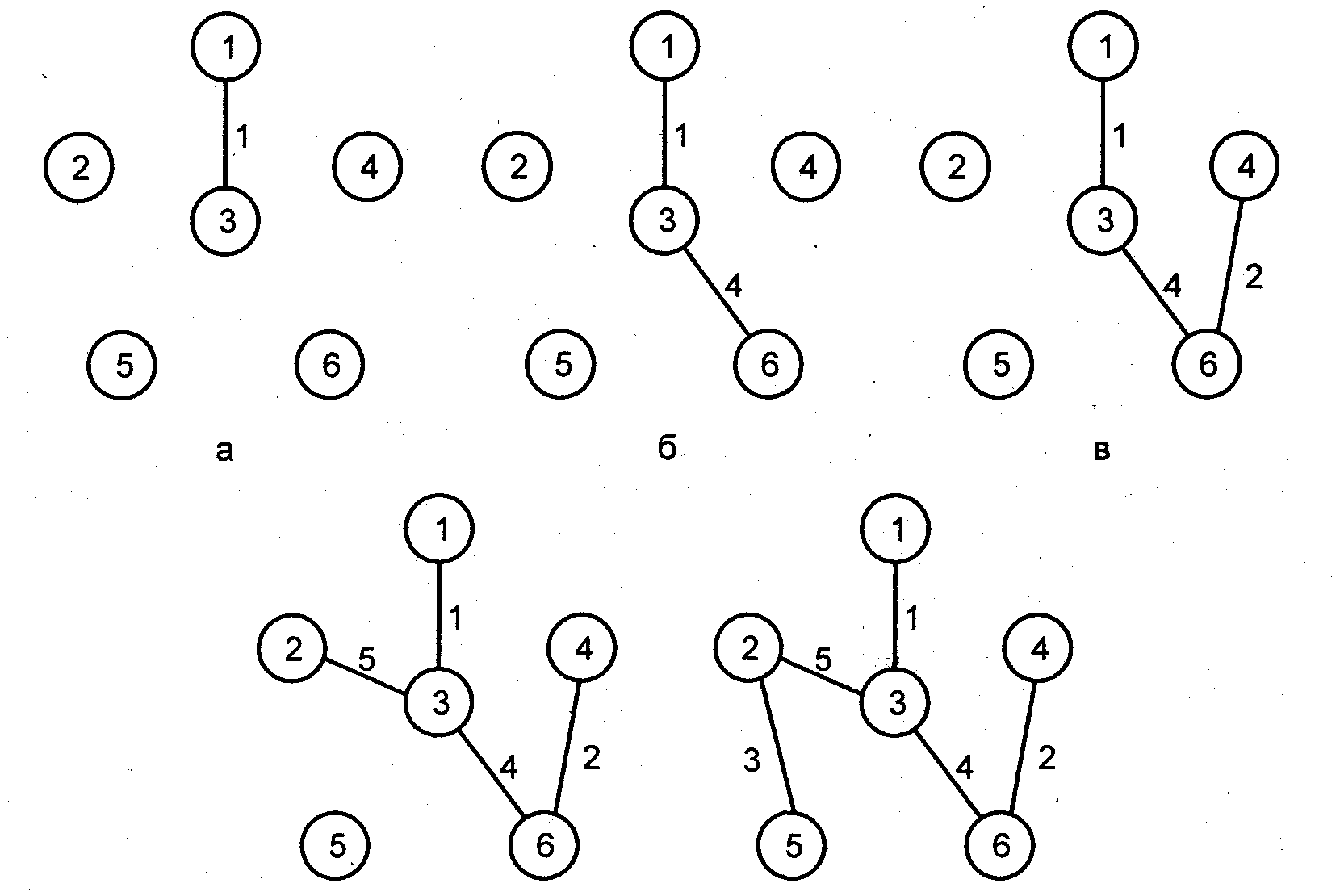
2. Построение остовного дерева минимальной стоимости (алгоритм Крускала):

В алгоритме Крускала построение остовного дерева минимальной стоимости для графа G начинается с графа Т = (V,), состоящего только из n вершин графа G и не имеющего ребер. Таким образом, каждая вершина является связной (с самой собой) компонентой. В процессе выполнения алгоритма набор связных компонент, постепенно объединяясь, формирует остовное дерево.

При построении связных, постепенно возрастающих компонент поочередно проверяются ребра из множества Е в порядке возрастания их стоимости. Если очередное ребро связывает две вершины из разных компонент, тогда оно добавляется в граф Т. Если это ребро связывает две вершины из одной компоненты, то оно отбрасывается, так как его добавление в связную компоненту, являющуюся свободным деревом, приведет к образованию цикла. Когда все вершины графа G будут принадлежать одной компоненте, построение остовного дерева минимальной стоимости Т для этого графа заканчивается.

Последовательность построения остовного дерева минимальной стоимости приведена ниже.