
- •Понятие первообразной и неопределенного интеграла. Теорема о совокупности первообразных. Свойства неопределенного интеграла. Таблица интегралов.
- •Интегрирование подстановкой и по частям в неопределенном интеграле.
- •Инегрирование рациональных дробей.
- •Интегрирование некоторых тригонометрических функций и некоторых иррациональностей.
- •Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла.
- •7. Интегрирование подстановкой и по частям в опред интеграле
- •8. Теорема о производной от интеграла по переменному верхнему пределу.
- •9. Формула Ньютона – Лейбница.
- •10. Геометрические приложения определенных интегралов
- •11. Интеграл с бесконечным промежутком интегрирования
- •12.Дифференциальные уравнения 1 порядка.
- •13.Дефференциальные уравнения с разделяющимися переменными.
- •14. Однородные д.У первого порядка.
- •15. Линейные д.У 1 порядка
- •19. Однородные д.У с постоянными коэффициентами.
- •Линейное неоднородное уравнение с постоянными коэффициентами
- •20, Линейные неоднородные д.У. Теорема об общем решении.
- •22. Комплексные числа и действия над ними. Формы записи комплексных чисел, возведение в степень. И извлечение корня из комплексного числа.
- •Арифметические действия с комплексными числами
- •Алгебраическая форма записи комплексного числа
- •Извлечение корня квадратного из отрицательного числа
- •Возведение в степень комплексного числа
- •23. Понятие фнп. Предел функции в точке. Непрерывность функции в точке.
- •24. Частные производные. Производные высших порядков. Теорема о смешанных частных производных.
- •25. Дифференциал функции двух переменных.
- •26. Производная сложной функции.
- •27. Дифференцирование функции, заданной неявно.
- •28. Скалярное поле. Линии уровня. Производная по направлению.
- •29. Градиент и его свойства.
- •30. Экстремум функции нескольких переменных. Необходимое условие экстремума.
- •31. Квадратичная форма. Критерий Сильвестора. Достаточное условие экстремума.
- •32. Числовые ряды. Необходимый признак сходимости числового ряда. Свойства числовых рядов.
- •33. Признаки сравнения для положительных числовых рядов.
- •34. Признак Даламбера.
- •35. Интегральный признак Коши.
- •36. Знакопеременные ряды. Абсолютная и условная сходимость.
- •37. Знакочередующиеся ряды. Признак Лейбница.
- •38. Степенные ряды. Теорема Абеля. Радиус сходимости.
- •39. Формула Тейлора, ряд Тейлорв.
7. Интегрирование подстановкой и по частям в опред интеграле
Интегрирование подстановкой
Теорема. Если

То
![]()
Пусть F(x) есть первообразная для f(x) на отрезке [a;b],

Интегрирование по частям
Теорема: если ф-ция u=u(x) имеют непрерывные производные на отрезке [a;b],то имеет место формула
![]()
8. Теорема о производной от интеграла по переменному верхнему пределу.
Если
в определенном интеграле
![]() изменять верхний предел b, то будет
меняться и значение интеграла, то есть
интеграл будет функцией верхнего
предела.
изменять верхний предел b, то будет
меняться и значение интеграла, то есть
интеграл будет функцией верхнего
предела.
Обозначим
верхний предел x, а переменную
интегрирования, чтобы не смешивать ее
с верхним пределом, обозначим t. Таким
образом, интеграл с переменным верхним
пределом является функцией от x:![]() Имеет место теорема:
производная интеграла с переменным
верхним пределом от непрерывной функции
равна подынтегральной функции, в которой
переменная интегрирования заменена
верхним пределом:
Имеет место теорема:
производная интеграла с переменным
верхним пределом от непрерывной функции
равна подынтегральной функции, в которой
переменная интегрирования заменена
верхним пределом:
![]()
Доказательство. По определению производной
![]() где
где
![]()
[первый интеграл представим в виде суммы двух интегралов, пользуясь свойством аддитивности]=
![]()
![]() [по
теореме о среднем]=
[по
теореме о среднем]=
![]() где
где![]() Тогда
Тогда
![]() следует из определения непрерывной
функци, т.к. при
следует из определения непрерывной
функци, т.к. при
![]()
![]()
Таким
образом,
![]() Это
значит, что интеграл с переменным верхним
пределом
Это
значит, что интеграл с переменным верхним
пределом
![]() является первообразной для функции
f(x).
является первообразной для функции
f(x).
9. Формула Ньютона – Лейбница.
Сравнивая две формулы для площади криволинейной трапеции, приходим к следующему заключению: если F ( x ) - первообразная функции f ( x ) на отрезке [ a, b ] , то
формула справедлива для любой функции f ( x ), непрерывной на отрезке [ a, b ] .
10. Геометрические приложения определенных интегралов
Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [a;b] изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с є (а; b) на части [а; с] и [с; b] значение величины А, соответствующее всему отрезку [а; b], равно сумме ее значений, соответствующих [а; с] и [с; b].
Первая схема базируется на определении определенного интеграла.
1. Точками х0 = а, x1,..., xn = b разбить отрезок [а;b] на n частей. В соответствии с этим, интересующая нас величина А разобьется на n «элементарных слагаемых» ΔAi (i = 1,...,n): А = ΔA1+ΔА2 +...+ ΔАn.
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ΔAi ≈ ƒ(ci)Δxi.
Получим приближенное значение величины А
в виде интегральной суммы:
3. Искомая величина А равна пределу
11. Интеграл с бесконечным промежутком интегрирования
Определение
несобственного интеграла по бесконечному
промежутку. Пусть функция f(x) определена
на полуоси
![]() и интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
и интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
![]() при
при
![]() наз
несобственным интегралом функции f(x)
от a до
наз
несобственным интегралом функции f(x)
от a до
![]() и
обозначается
и
обозначается
![]()
По
определению,
![]()
Если
этот предел существует и конечен,
интеграл
![]() наз
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
наз
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
-
Если на промежутке [a;+∞) непрерывные ф-ции f(x) и фи(x) удовлетворяют условию 0≤f(x)≤фи(x) то из сходимости интеграла
 следует
сходимость интеграла
следует
сходимость интеграла
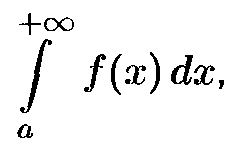 ,
а из расходимости интеграла
,
а из расходимости интеграла
 следует
расходимость интеграла
следует
расходимость интеграла

-
Если сущ предел

 то
интегралы
то
интегралы
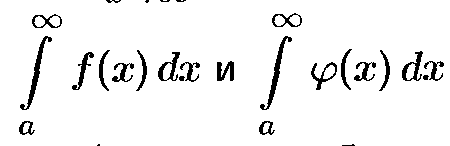 одновременно оба сходятся или оба
расходятся
одновременно оба сходятся или оба
расходятся
