Билет 38.

Окружность Аполлония –геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек – величина постоянная.

Пусть на плоскости даны две точки и 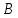. Рассмотрим все точки 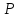этой плоскости, до каждой из которых . При 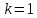эти точки заполняют срединный перпендикуляр к отрезку 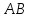; в остальных случаях указанное геометрическое место – окружность, называемая окружностью Аполлония.

Свойства окружности Апполония

1. Радиус окружности Апполония равен .

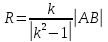2. Отрезок между точкой на окружности и точкой пересечения ее с прямой 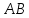является биссектрисой самого угла 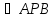или угла, смежного с ним.

Билет 39. Теорема Чевы

Определение: В произвольном треугольнике 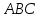на сторонах 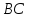, , 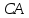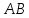взяты соответственно точки 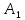, , , 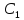тогда выполняются следующие два равносильных утверждения:

а) прямые 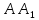, , 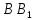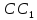пересекаются в некоторой точке треугольника ;

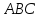б)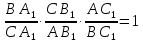 (Условие Чевы)

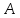
Доказательство: Доказать теорему Чевы проще всего, заменив от­ношения отрезков в условии Чевы на отношение площадей:

Следовательно,

Точно так же получим, что

Теперь осталось только перемножить эти три равенства:

.

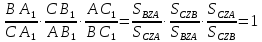Обратная теорема Чевы

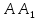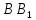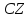Пусть и пересекаются в точке . Пусть прямая пересекает сторону 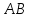треугольника в точке 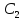. Для точек 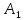, , 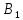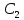выполняется условие Чевы.

Билет 40.

Построение касательной к окружности

Касательную из точки 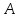к окружности можно провести следующим образом:

1. На отрезке 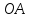как на диаметре строят окружность радиуса ;

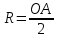2. Точки 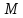и пересечения полученной окружности с заданной определяют положение точек касания;

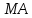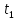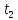3. Отрезки и  определяют положение касательных и проведенных из точки 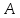к окружности.

Билет 41.

Выражение координат середины отрезка через координаты его концов

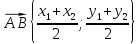
Билет 42.

Радиус вписанной в треугольник и описанной вокруг него окружности

Исходя из формулы 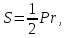получаем .

Радиус описанной окружности *

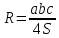*Примечание: к сожалению, эксперты Волшебной Формулы не смогли найти доказательство данной теоремы.

Билет 43.

Вывод формулы окружности

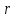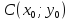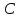Выведем формулу окружностью с радиусом и центром . Расстояние от точки до произвольной точки 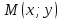всегда можно найти по формуле 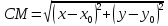. Если 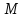лежит на данной окружности, то 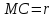, или 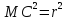. Отсюда 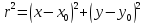. В частности, уравнение окружности с центром в начале координат имело бы вид .

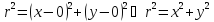Билет 44.

Правильный многоугольник – такой многоугольник, стороны которого равны.

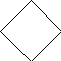
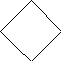
Построение квадрата

Построим на плоскости окружность и проведем ее диаметр. Затем построим другой диаметр, перпендикулярный** предыдущему. Соединив точки пересечения диаметра, мы получаем квадрат. Для того чтобы получить квадрат со стороной 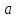, нужно строить окружность с диаметром .

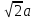** см. Билет 28.

Схема построения квадрата:

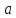
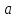
Построение правильного шестиугольника со стороной

Построим окружность с радиусом 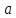. Затем, возьмем любую точку лежащую на данной окружности, и построим другую окружность того же радиуса с центром в этой точке. Затем построим другую окружность того же радиуса в центре с точкой пересечения предыдущей окружности с первой окружностью. Подобно тому, как мы строили эту окружность, построим еще три таких же. Соединив точки пересечения получившихся окружностей с исходной, получаем правильный шестиугольник.

Схема построения правильного шестиугольника:

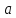
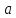
Билет 45.

Построение прямой, параллельной данной

Задача: Даны прямая 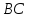, и точка 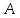такая, что 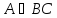. Построить прямую, параллельную прямой 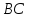, и проходящую через точку .

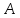Решение: Построим перпендикуляр* 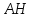из точки 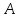к прямой 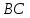. Затем отложим другой перпендикуляр к 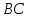, и отметим на нем отрезок , равный 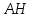, причем 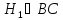. Тогда прямая, проведенная через точки 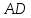будет параллельна .

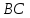* см. Билет 28.

Билет 46.

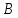
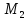
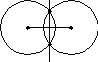
Способ 1) см. Билет 13.

Способ 2) Проведем из концов отрезка две окружности одинакового радиуса, как показано на рис.46.1. Прямая, проходящая через общие точки этих окружностей и 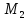рассекает данный отрезок равно напополам.

Рис.46.1

Билет 47.

Два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.

Два угла с общей вершиной, одна из сторон которых – общая, а оставшиеся стороны лежат на одной прямой, называются смежными. Сумма смежных углов равна .

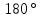Билет 48.

Описанный четырехугольник – это четырехугольник, в который вписана окружность.

В выпуклый четырёхугольник 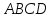можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: .
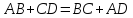