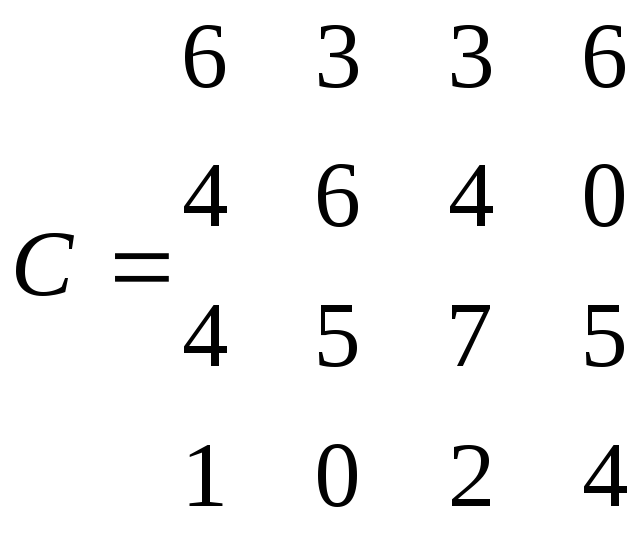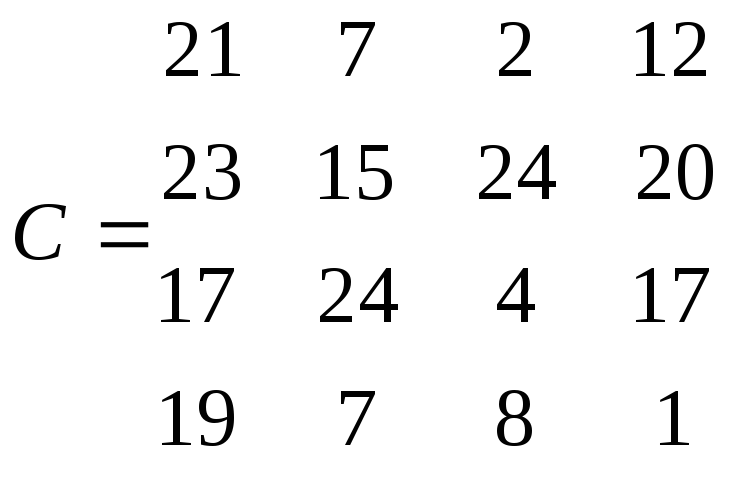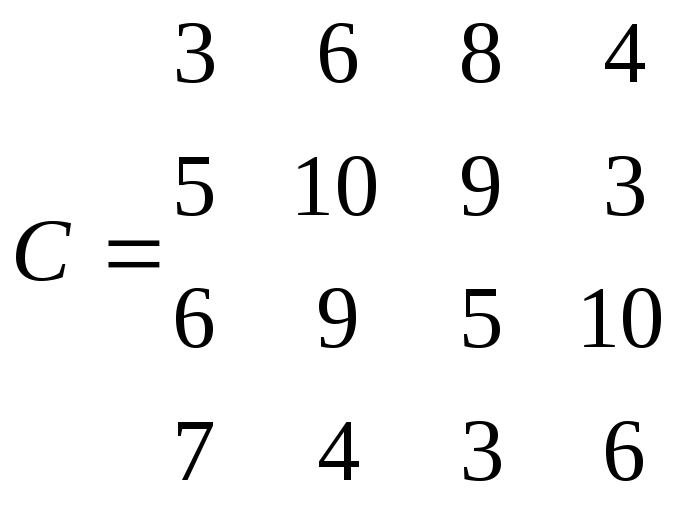Завдання №6 Розв’язок задач дискретного програмування методом Гоморі та методом віток та границь
Завдання: розв’язати задачу дискретного програмування наступними методами:
а) методом Гоморі;
б) методом віток і границь.
|
№ |
Задача |
№ |
Задача |
№ |
Задача |
|
|
1 |
L=2x1+3x2→max 3x1+5x2≤60 3x1+4x2≤34 x2≤8 xi>0єZ |
2 |
L=2x1-8x2→max 3x1+5x2≤17 x2≤4 xi>0єZ |
3 |
L=x1+x2→max 8x1-3x2≤24 3x1+2x2≤13 xi>0єZ |
|
|
4 |
L=7x1-9x2→max 2x1+x2≤9 4x1+5x2≤5 3x2≤7 xi>0єZ |
5 |
L=3x1+x2→max 4x1+3x2≤18 x1+2x2≤6 xi>0єZ |
6 |
L=8x1+6x2→max 3x1+5x2≤11 4x1+x2≤8 xi>0єZ |
|
|
7 |
L=x1+2x2→max 2x1+2x2≤7 4x1-5x2≤9 xi>0єZ |
8 |
L=2x1+7x2→max 2x1+2x2≤9 -x1≤-3 -x2≤-4 xi>0єZ |
9 |
L=2x1+x2→max 2x1+6x2≤15 4x1+3x2≤11 xi>0єZ |
|
|
10 |
L=x1+x2→max x1+3x2≤30 2x1+x2≤20 xi>0єZ |
11 |
L=-x1+4x2→max -3x1-5x2≤-8 -3x1+10x2≤16 xi>0єZ |
12 |
L=-x1+3x2→max -x1+2x2≤6 x1+2x2≤5 xi>0єZ |
|
|
13 |
L=-x1+3x2→max x1+x2≤3 -x1+2x2≤5 xi>0єZ |
14 |
L=5x1+x2→max 3x1+6x2≤11 x1≤3 3x2≤1 xi>0єZ |
15 |
L=2x1+4x2→max 4x1+4x2≤15 x1+6x2≤7 xi>0єZ |
|
|
16 |
L=4x1+6x2→max x1+15x2≤32 2x1≤31 x2≤2 xi>0єZ |
17 |
L=4x1+3x2→max 3x1+5x2≤60 3x1+5x2≤34 x2≤7 xi>0єZ |
18 |
L=2x1-7x2→max 3x1+4x2≤17 2x2≤5 xi>0єZ |
|
|
19 |
L=x1+3x2→max 7x1-3x2≤24 3x1+x2≤14 xi>0єZ |
20 |
L=7x1-5x2→max 4x1+x2≤9 4x1+3x2≤11 3x2≤7 xi>0єZ |
21 |
L=3x1-2x2→max x1+3x2≤18 5x1+2x2≤9 xi>0єZ |
|
|
22 |
L=5x1+6x2→max 3x1+2x2≤11 4x1-x2≤7 xi>0єZ |
23 |
L=7x1+2x2→max 2x1-2x2≤7 4x1+5x2≤9 xi>0єZ |
24 |
L=-2x1+3x2→max 2x1+x2≤9 -4x1≤-3 -x2≤-4 xi>0єZ |
|
|
25 |
L=2x1+3x2→max 2x1+9x2≤15 x1+3x2≤11 xi>0єZ |
26 |
L=3x1+x2→max x1+4x2≤31 2x1+x2≤25 xi>0єZ |
27 |
L=-3x1+4x2→max -3x1+5x2≤8 -x1+7x2≤15 xi>0єZ |
|
|
28 |
L=-5x1+3x2→max -x1+4x2≤6 3x1+2x2≤5 xi>0єZ |
29 |
L=x1-3x2→max x1+x2≤4 -3x1+2x2≤9 xi>0єZ |
30 |
L=6x1+x2→max 3x1+5x2≤13 2x1≤3 3x2≤1 xi>0єZ |
|
Завдання №7 Розв’язок задач дискретного програмування методом Мака та Угорським методом
Завдання: розв’язати задачу дискретного програмування наступними методами:
а) методом Мака;
б) Угорським методом,
а саме розв′язати задачу про оптимальні призначення з заданою матрицею витрат С.
|
№ |
Задача |
№ |
Задача |
№ |
Задача |
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
