Задание на курсовую работу (вариант 5)

В курсовой работе следуем выполнить задания:

1. Рассчитать электрический LC-фильтр по заданным параметрам.

2. Получить соотношения для комплексного коэффициента передачи и импульсной характеристики полученного фильтра.

3. Проанализировать прохождение периодической последовательности прямоугольных импульсов через полученный фильтр.

Технические требования на проектирование фильтра:

1. Тип фильтра: полосовой.

2. Тип аппроксимации: по Баттерворту.

3. Тип реализации: по Дарлингтону.

4. Граничные частоты полосы пропускания: f₂=5,0 кГц; f₂’=2,4 кГц.

5. Граничная частота полосы непропускания: f₃=7,0 кГц.

6. Максимальное затухание в полосе прозрачности фильтра: ΔA=0,7 дБ.

7. Минимальное затухание в полосе непрозрачности: A_min=20 дБ.

8. Сопротивление нагрузки: R₂=700 Ом.

СОДЕРЖАНИЕ

	ВВЕДЕНИЕ	4
1.	Синтез электрического фильтра	5
1.1.	Переход к ФНЧ-прототипу и нормирование частот	5
1.2.	Аппроксимация рабочей передаточной функции и характеристики рабочего ослабления фильтра	5
1.3.	Реализация схемы ФНЧ-прототипа	6
1.4.	Переход от ФНЧ-прототипа к схеме заданного фильтра	8
1.5.	Расчет и построение денормированных частотных характеристик	9
2.	Анализ прохождения периодического сигнала через фильтр	12
2.1.	Расчет спектра входного сигнала	12
2.2.	Расчет сигнала на выходе фильтра в частотной области	14
2.3.	Расчет сигнала на выходе фильтра во временной области	15
	ЗАКЛЮЧЕНИЕ	18
	СПИСОК ЛИТЕРАТУРЫ	19

ВВЕДЕНИЕ

В современных системах связи широко применяются электрические фильтры: LC-фильтры, активные RC-фильтры, пьезоэлектрические, пьезокерамические, магнитострикционные, электромеханические, волноводные, цифровые фильтры и др. Причем, LC-фильтры занимают особое положение в силу ряда причин. Во-первых, эти фильтры широко применяются в различных частотных диапазонах. Во-вторых, для LC-фильтров существует хорошо разработанная методика расчета, и синтез большинства перечисленных выше фильтров во многом использует эту методику.

Задачей синтеза электрического фильтра является определение схемы фильтра, содержащей минимально возможное число элементов, которая удовлетворяла бы техническим требованиям.

В настоящее время используются две принципиально отличные методики расчета фильтров:

1. Расчет по характеристическим параметрам.

2. Расчет по рабочим параметрам (по рабочему ослаблению или рабочей фазовой постоянной).

Метод синтеза по рабочим параметрам позволяет получить электрический фильтр с меньшим числом элементов, чем расчет по характеристическим параметрам. Кроме того, метод расчета по рабочим параметрам является единственно возможным для RC-фильтров и, следовательно, является более общим методом. Следует отметить, что расчет по рабочим параметрам требует большей точности вычислений, что вызывает необходимость применения ЭВМ.

1. Синтез электрического фильтра

1.1. Переход к фнч-прототипу и нормирование частот

Средняя геометрическая частота полосового фильтра (ПФ):

Граничная частота полосы задержания (второе значение):

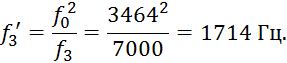
Нормированные частоты ФНЧ-прототипа:

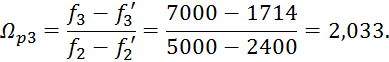
1.2 Аппроксимация рабочей передаточной функции и характеристики рабочего ослабления фильтра

Коэффициент неравномерности рабочего ослабления в полосе пропускания:

Порядок полинома Баттерворта:

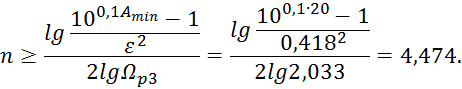
Окончательно выбираем порядок полинома:

Определяем корни полинома V(p) и функции T(p), лежащие в левой полуплоскости, используя соотношение:

Получаем значения корней полинома:

Формируем искомые функции T(p) и A(Ω_p):

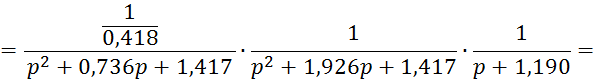
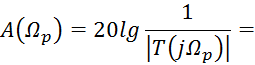
Выполним проверку аппроксимированной функции A(Ω_p) на частотах Ω_p1=0, Ω_p2=1 и Ω_p3=2,033:

1.3 Реализация схемы фнч-прототипа

Запишем выражение функции входного сопротивления для ФНЧ-прототипа:

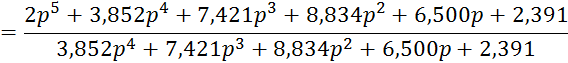
Выполним разложение функции Z_ВХ(p) в цепную дробь:

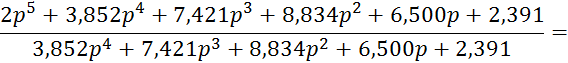
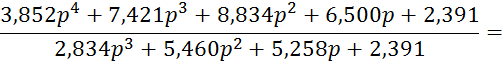
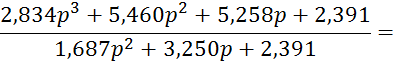
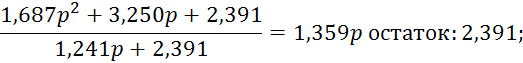
В результате преобразования получаем следующую цепную дробь:

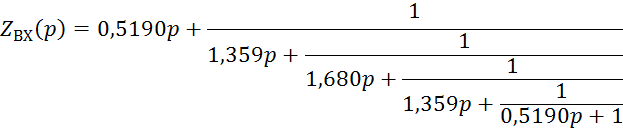
Полученной функции Z_ВХ(p) соответствует нормированная схема, изображенная на рисунке 1.

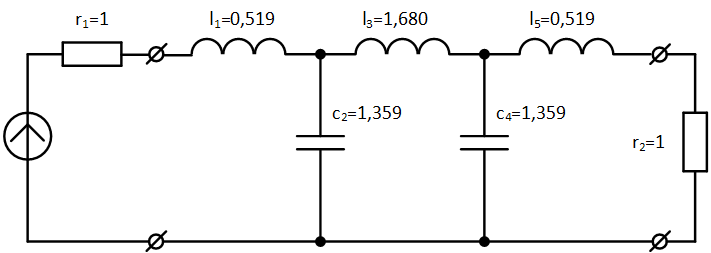
Рисунок 1 – Схема ФНЧ-прототипа

1.4 Переход от фнч-прототипа к схеме заданного фильтра

Осуществим переход от нормированной схемы ФНЧ-прототипа к схеме полосового фильтра (ПФ) – рисунок 2.

Рисунок 2 – Схема ПФ

Выполним расчеты параметров схемы ПФ:

Значения преобразующих множителей по сопротивлению и по частоте:

Коэффициенты денормирования K_l и K_c:

Определяем денормированные значения элементов схемы ПФ:

1.5 Расчет и построение денормированных частотных характеристик

Вывод соотношения для рабочего коэффициента передачи синтезированного фильтра приводит к громоздким соотношениям. Для упрощения конечного аналитического соотношения учтем, что схема синтезированного ПФ (рисунок 2) имеет лестничную структуру и симметрична. Коэффициент передачи лестничной структуры может быть определен как произведение частичных коэффициентов передачи для каждого отдельного звена схемы ПФ.

Предварительно введем соотношения:

Частичные коэффициенты передачи для лестничного ПФ:

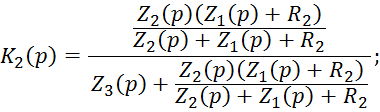
Коэффициент передачи всего фильтра:

График зависимости модуля коэффициента передачи от частоты изображен на рисунке 3.

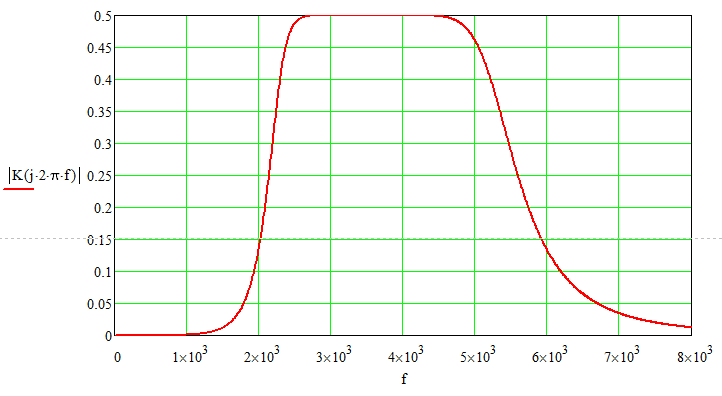
Рисунок 3 – График зависимости K(f)

Для расчета и построения графиков зависимостей A(f) и B(f) используем соотношения:

Полученные графические зависимости приведены на рисунках 4 и 5.

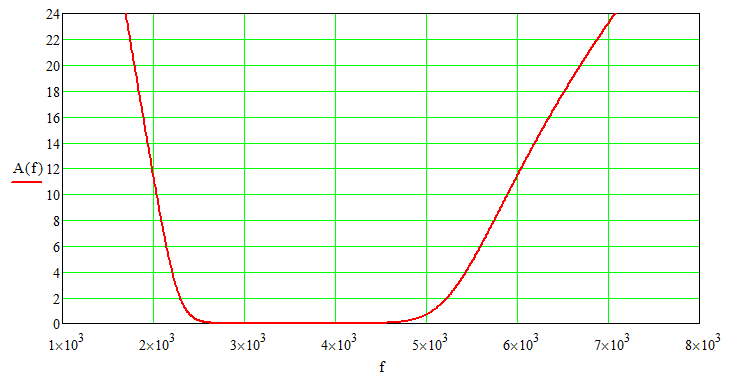
Рисунок 4 – График зависимости A(f)

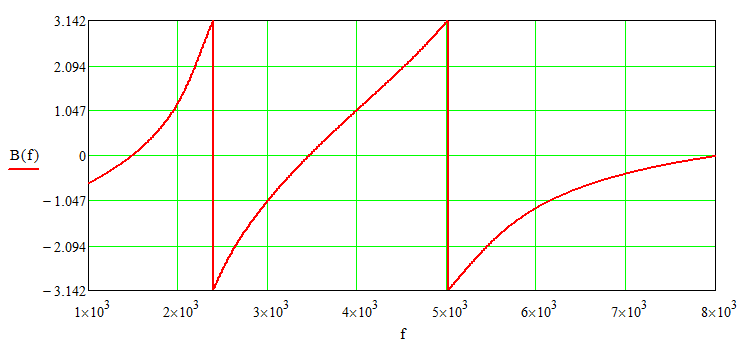
Рисунок 5 – График зависимости B(f)

2. Анализ прохождения периодического сигнала через фильтр

2.1. Расчет спектра входного сигнала

На вход синтезированного ПФ подана периодическая последовательность прямоугольных импульсов – рисунок 6.

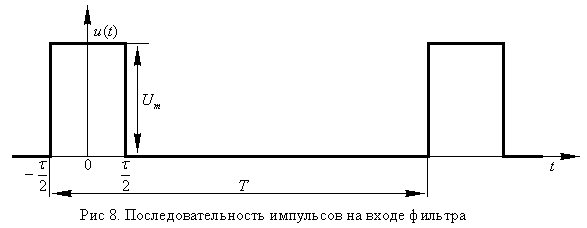
Рисунок 6 – Временная диаграмма входного сигнала

Заданы параметры прямоугольной последовательности импульсов:

Расчет спектра амплитуд последовательности прямоугольных импульсов можно осуществить по формуле:

Спектр фаз для заданной последовательности определяется соотношением:

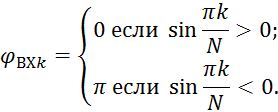
Амплитуда постоянной составляющей (нулевой гармоники):

Результаты расчетов сведем в таблицу 1.

Таблица 1 – Спектры сигналов

	Входной сигнал		Выходной сигнал
	UВХk, В	φВХk, рад	UВЫХk, В	φВЫХn, рад
0	0,2	-	0	-
1	0,374	0	0,014	-0,466
2	0,303	0	0,151	0
3	0,202	0	0,082	2,70
4	0,094	0	0,003	0,466
5	0	-	0	-
6	0,062	π	0,0001	2,67
7	0,086	π	0,00007	2,48
8	0,076	π	0,00003	2,35
9	0,042	π	0,000008	2,25
10	0	-	0	-

Правильность расчета спектра проверим путем построения графика входного сигнала путем суммирования первых 10 гармоник – рисунок 7. Для построения используем соотношение:

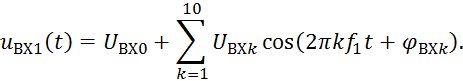
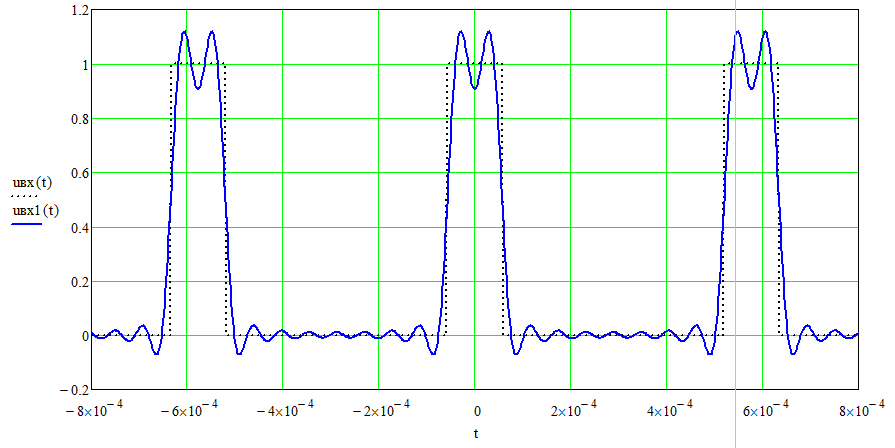
Рисунок 7 – Входной сигнал ПФ