
- •4. Какие бывают типы распределения и вариационных кривых?
- •19. Как вычисляют ошибку средней арифметической величины?
- •34. Определить среднюю величину семян тыквы одного сорта. Измерить длину (в мм) 50 взятых произвольно семян. Построить вариационную кривую.
- •49. Найти групповые, внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из следующих двух групп:
- •3). Найдем общую дисперсию
- •Список использованной литературы
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Приморская государственная сельскохозяйственная академия»
Институт животноводства и ветеринарной медицины
Кафедра: « Химии и генетики »
Контрольная работа
по дисциплине:
«Ветеринарная генетика»
Выполнил:
Уссурийск 2017 г.
4. Какие бывают типы распределения и вариационных кривых?
Нормальное распределение. Большинству количественных признаков и свойств сельскохозяйственных и биологических объектов с непрерывным характером варьирования присуще нормальное распределение.
Сущность нормального распределения заключается в том, что наибольшее число вариант расположено в центре распределения около среднего значения признака. Чем больше отклоняются значения отдельных вариант от среднего значения признака, тем реже они встречаются, т. е. вероятность встречаемости той или иной варианты уменьшается по мере ее удаления от средней величины. В любом стаде животных особей со средним значением признака (удой, процент жира, процент белка, живая масса, настриг шерсти и т. д.) больше, чем с очень низкой или высокой величиной признака. Нормальное распределение полностью характеризуется средней арифметической и средним квадратическим отклонением.
С увеличением объема совокупности вариационная кривая приближается к идеальной кривой, называемой кривой нормального распределения или нормальной вариационной кривой (рис. 1). Если из наивысшей точки кривой нормального распределения опустить перпендикуляр, то получится ее ось симметрии. Основание этого перпендикуляра совпадает со средним значением признака (х), медианой (Me) и модой (Мо). Весь диапазон изменчивости признака от средней арифметической охватывается шестью^сигмами (х ± За). Отклонение в обе стороны от средней на ± 1ст"*содержит 68,3 % всех вариант данного ряда, на±2а — 95,5 и на ± За - 99,7 %.
Биномиальное распределение. Если вероятности появления отдельных вариант выражаются величинами, соответствующими коэффициентам разложения бинома Ньютона, то такое распределение называется биномиальным. Оно относится к признакам, варьирующим дискретно, прерывисто (количество больных особей, количество самок и самцов в помете и т. д.). В этом случае частоты отдельных классов пропорциональны коэффициентам разложения бинома Ньютона:
(Р + Ч)к,
где р и q — вероятности появления каждого признака; к — число классов, отличающихся по появлению признака.
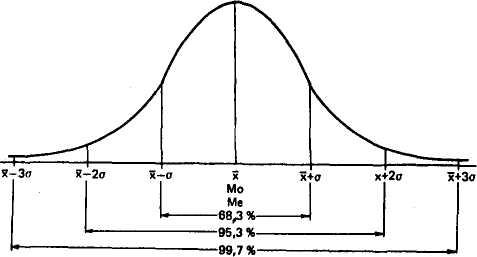
Рис. 1. Стандартизованная форма нормальной вариационной кривой
Если р = 0,5, q = 0,5, а к увеличивается, то биномиальная кривая приближается к нормальной кривой, которая является пределом биномиального распределения. Чем больше различаются значения р и q, тем значительнее асимметрия биномиальной кривой. Средняя арифметическая и среднее квадратическое отклонение характеризуют биномиальное распределение.
Пример. В одном хозяйстве изучено распределение семейств по количеству больных туберкулезом коров (табл. 1). Каждое семейство состояло из S особей.
Таблица.1. Распределение семейств по количеству больных туберкулезом коров
|
Число бальных (v) |
5 |
4 |
3 |
2 | |
|
о |
* = 5 |
|
Число семейств (/) yf |
1 5 |
1 4 |
3 9 |
12 24 |
5 5 |
3 0 |
2/=л = 25 Zi/=47 |
Среднее количество туберкулезных коров в семействе х = QLyf): л = 47 \_ 25 = = 1,88. По формуле х=кр доля больных коров в семействе равна р = х: к = = 1,88 : 5 = 0,38, а здоровых — а = 1 —а == 1 — 0.38 = 0,62. Находим среднее квадратическое отклонение о = -fkpq = V5-0,38-0,62 = VI, 18 = 1,08. Так как данный ряд является рядом разложения бинома Ньютона (0,38 + 0,62) при л = 25, то можно вычислить теоретическую частоту распределения семейств по количеству больных туберкулезом коров. По треугольнику Паскаля коэффициенты бинома для к = 5:, 1, 5, 10, 5, 1. Получаем следующие показатели вероятности: (0,38 + 0.62)5 = l-d,385 + S-0,38^0,62 + 10,62s = 0,0079 + 0,0645 + 0,2106 + 0,3441 + 0,2808 + 0,0916. Чтобы получить теоретическое распределение семейств, нужно умножить полученные показатели вероятности на число исследованных семейств (л = 25):-= wi:0,0079-25 = 0,2; 0,0645-25 = 1,6; 0,2106-25 = 5,3; 0,3441-25 0,2808-25 = 7,0; 0,0916-25 = 2,3.
|
Фактическое распределение |
1 |
1 |
3 |
12 |
5 |
3 |
|
Теоретически ожидаемое |
0,2 |
1,6 |
5,3 |
8,6 |
7,0 |
2,3 |
|
распределение |
|
|
|
|
|
|
Степень соответствия фактического распределения теоретически ожидаемому определяют с помощью метода хи-квадрат.
Распределение Пуассона. Это распределение относится к дискретной изменчивости, к редким событиям. Такими событиями являются мутации, наследственные дефекты, рождение троен у крупного рогатого скота и т. д. Поэтому при распределении Пуассона значение р очень мало (так как событие совершается редко), а значение q приближается к единице.
Распределение Пуассона характеризуется одним параметром — средней арифметической (х), потому что а 2 равна или мало отличается от х. С помощью распределения Пуассона можно рассчитать вероятность появления в стаде или породе наследственных дефектов. Для этого используют формулу= —,е-х, или Pm =где т — число появлений редко встречающегося события в я независимых повторных испытаниях; е = 2,7183... — основание натуральных логарифмов; х — среднее число появлений редкого события (х = пр); ! — факториал частоты, или произведение натуральных чисел (1 • 2 ■ З...т).
Если в популяции вероятность появления наследственного уродства р = 0,002, то можно определить вероятность появления 3, 2, 1, 0 уродов среди, например, 200 телят. Среднее число появления уродов х = пр = 200 ■ 0,002 = 0,4 головы в изучаемой совокупности. Вероятность рождения трех уродов
Рт3 = 0,0072.
о,43 _ 0,064 _ 0,064
3!-2,71830-4 1-2-3-2.71830-4 61,491
Таблица.2. Значение вероятности появления редких событий при распределении
Пуассона
|
Число редких |
Среднее число редких событий (х) | ||||||
|
событий (/я) |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 | 1,0 |
1,5 |
2,0 |
|
0 |
9048 |
8187 |
7408 |
6703 |
6065 |
3679 |
2231 |
1353 |
|
1 |
0905 |
1637 |
2222 |
2681 |
3033 |
3679 |
3347 |
2707 |
|
2 |
0045 |
0164 |
0333 |
0536 |
0758 |
1839 |
2510 |
2707 |
|
3 |
0002 |
ООП |
0033 |
0072 |
0126 |
0613 |
1255 |
1804 |
|
4 |
0000 |
0001 |
0003 |
0007 |
0016 |
0153 |
0471 |
0902 |
Примечание. В табл.2. нуль целых и запятая опущены. Когда известны х и т, то по таблице 15 находим, что при х = = 0,4 и т = 3 вероятность появления трех уродов Ртз = 0,0072. Вероятность появления двух уродов — Ртг = 0,0536, одного — Ргщ = 0,2681 и отсутствие уродов — Рто = 0,6703.
Трансгрессивные ряды. Они характеризуются тем, что две или несколько кривых вариационных рядов лежат не отдельно, а заходят в большей или меньшей части друг на друга. Если два трансгрессивных ряда объединить и построить вариационную кривую, то обычно образуется двухвершинная кривая (рис. 2). В данном примере она указывает на то, что бурые латвийские и джерсейские помесные коровы различаются по содержанию жира в молоке, но часть животных имеет одинаковую жирномолочность.
Бывают случаи, когда сильно различающиеся трансгрессивные ряды не обнаруживают двухвершинности. Чем больше трансгрессия, тем более сходны два вариационных ряда. Если
трансгрессия отсутствует, то кривые не соприкасаются друг с другом. При изучении изменчивости нельзя объединять в одну группу животных разных пород, неодинакового возраста, выращенных в различных условиях среды и т. д.
ЖИРНОСТЬ МОЛОКА, % -
3, 4.
3, 6.
4, 0.
4, 6.
5, 0.
5, 4.
5, 8.

Рис. 2. Двухвершинная кривая распределения по содержанию жира в молоке коров одного хозяйства, построенная без учета их породы, и кривые распределения по каждой из двух пород в отдельности (по О. А. Ивановой, 1974):
1 — по всему стаду; 2 — помеси с джерсейской породой; 3 — коровы бурой латвийской породы
