13.2. Закон Ампера

Одним из главных проявлений магнитного поля является его силовое действие на движущиеся электрические заряды и токи.В результате обобщения многочисленных опытных данных А. М. Ампером был установлен закон, определяющий это силовое воздействие.

Приведем его в дифференциальной форме, что позволит вычис­лять силу, действующую на различные контуры с током, располо­женные в магнитном поле.

В проводнике, находящемся в магнитном поле, выделим достаточно малый участок , который можно рассматривать как вектор, направленный по току (рис. 13.5). Произведение называют элементом тока. Сила, действующая со стороны магнитного поля на элемент тока,

(13.9)

где k — коэффициент пропорциональности; в СИk = 1, поэтому

(13.10)

или в векторной форме

(13.11)

Для плоского контура с током находим силу, действующую на участок l проводника со стороны магнитного поля, интегрированием скалярного выражения (13.10):

(13.12)

Соотношения (13.9)—(13.12) выражают закон Ампера.

Рис. 13.5 Рис. 13.6

Рассмотрим некоторые примеры на применение формулы (13.11).

1. Прямолинейный участок проводника с током I длиной l, расположенный в однородном магнитном поле под угломк магнитной индукции (рис. 13.6). Для нахождения силы, действую­щей на эту часть проводника со стороны магнитного поля, интег-оиоуем (13.12) и получаем

(13.13)

2. Прямоугольная рамка KLMN с током I, помещенная в одн­родное магнитное поле индукции (рис. 13.7, а). Пронумеруем стороны рамки и обозначим силы, действующие на них со стороны магнитного поля,F₁, F₂, F₃, F₄.

Силы F₁ и F₃, приложенные к серединам соответствующих сторон, направлены противоположно вдоль оси и по формуле (13.13) равны. Силы же F₂ = F₄ = IBb создают пару сил, момент которой (рис. 13.7, б)

М = IBb (a/2) sin + IBb(a/2) sin = IBbasin. (13.14)

Так как Iba = IS = p_m, то из (13.14) имеем

M=p_mBsin, (13.15)

или в векторной форме

(13.16)

Фактически на основе этой зависимости в § 13.1 было введено понятие вектора магнитной индукции.

13.3. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца

Сила, действующая, согласно закону Ампера, на проводник с током в магнитном поле, есть результат его воздействия на движущиеся электрические заряды, создающие этот ток.

Р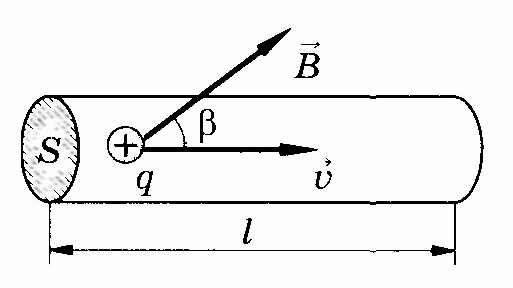ассмотрим цилиндрический проводник длинойl с токомI,расположенный в магнитном поле индукции (рис. 13.8). Скорость направленного движения некоторого положительного заряда q равна . Сила, действующая на отдельный движущийся заряд, определяется отношением силы F, приложенной к проводнику с током, к общему числу .N этих зарядов в нем:

(13.17)

Рис. 13.8

Раскроем выражение для силы, используя (13.13) и полагая, что сила тока равна

где j — плотность тока. Учитывая (12.50), получаем

(13.18)

где п = N/(Sl) — концентрация частиц. Подставляя (13.18) в (13.17), получаемвыражение для силы, действующей со стороны магнитного поля на отдельный движущийся электрический заряд и называемой силой Лоренца:

Направление силы Лоренца можно определить из векторной записи уравнения (13.19) с учетом знака заряда q:

(13.20)

Как видно из (13.20), эта сила всегда перпендикулярна плоскос­ти, в которой лежат векторы и . Из механики известно, что если сила перпендикулярна скорости, то она изменяет лишь ее направление, но не значение. Следовательно, сила Лоренца не изменяет кинетической энергии движущегося заряда и не совершает работы.

Если заряд неподвижен относительно магнитного поля или его скорость параллельна (антипараллельна) вектору магнитной индукции, то сила Лоренца равна нулю.

Пусть в однородное магнитное поле перпендикулярно векторуиндукции влетает со скоростью v положительно заряженная частица (рис. 13.9). На нее действует сила Лоренца f_Л, которая вызовет центростремительное ускорение, и, по второму закону Ньютона,

m²/r=qB, (13.21)

где q и т — заряд и масса частицы, r — радиус траектории, по которой она будет двигаться. Из (13.21) получаем

Рис. 13.9 r = m/(qB). (13.22)

Отсюда следует, что радиус траектории остается постоянным, а сама траектория есть окружность.

Используя (13.22) и считая, что значение скорости частицы не изменяется, найдем период вращения ее по окружности:

(13.23)

Отношение q/m называют удельным зарядом частицы. Период вращения ее в магнитном поле [см. (13.23)] не зависит от радиуса окружности и скорости, а определяется только магнитной индукцией и удельным зарядом. Эту особенность используют в ускорителе заряженных частиц — циклотроне.

Чтобы описать форму траектории заряженной частицы, влетающей со скоростью в однородное магнитное поле под произвольным углом к (рис. 13.10), разложим вектор и на две составляющие и _|| и _, направленные соответственно вдоль вектора магнитной индукции магнитного поля и перпендикулярно ему. Составляющая _|| при движении частицы в магнитном поле остается постоянной; сила Лоренца, действующая на частицу, изменит направление составляющей скорости _. Под действием этой силы частица вращается по окружности. Таким образом, траекторией движения будет винтовая линия — вращение по окружности со скоростью _ совместно с перемещением вдоль вектора магнитной индукции со скоростью _||.

Если на движущуюся заряженную частицу q действуют электрическое поле с напряженностью и магнитное поле с магнитнойиндукцией (рис. 13.11), то результирующая сила равна

(13.24)

Во многих системах (осциллограф, телевизор, электронный микроскоп) осуществляют управление электронами или другими заряженными частицами, воздействуя на них электрическими и магнитными полями, в этом случае основной расчетной формулой является (13.24).