
- •Теория вероятностей
- •§2.1. Случайное событие. Вероятность
- •§ 2.2. Случайная величина. Закон распределения. Числовые характеристики
- •§ 2.3. Нормальный закон распределения
- •§ 2.4. Распределения Максвелла и Больцмана
- •Лекция 2.
- •Математическая статистика
- •§3.1. Основные понятия математической статистики
- •§ 3.2. Оценка параметров генеральной совокупности по ее выборке
- •§3.3. Проверка гипотез
- •§ 3.4. Корреляционная зависимость. Уравнения регрессии
- •Лекция 3.
- •Механические колебания и волны.
- •5.1. Свободные механические колебания (незатухающие и затухающие)
- •5.2. Кинетическая и потенциальная энергии колебательного движения
- •5.3. Сложение гармонических колебаний
- •5.4. Сложное колебание и его гармонический спектр
- •5.5. Вынужденные колебания. Резонанс
- •5.6. Автоколебания
- •5.7. Уравнение механической волны
- •5.8. Поток энергии и интенсивность волны
- •5.9. Ударные волны
- •5.10. Эффект Доплера
- •Лекция 4
- •Акустика
- •6.1. Природа звука и его физические характеристики
- •§ 6.2. Характеристики слухового ощущения. Понятие об аудиометрии.
- •§ 6.3. Физические основы звуковых методов исследования в клинике
- •§ 6.4. Волновое сопротивление. Отражение звуковых волн. Реверберация
- •§ 6.5. Физика слуха
- •6.6. Ультразвук и его применения в медицине
- •6.7. Инфразвук
- •6.8. Вибрации
- •Лекция 5
- •Течение и свойства жидкостей
- •Уравнение Бернулли.
- •1. Схема трубки тока жидкости для вывода формулы Бернулли.
- •1)Наклонная трубка тока постоянного сечения.
- •2)Горизонтальная трубка тока переменного сечения.
- •3) Измерение скорости жидкости. Трубка Пито.
- •7.1. Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости
- •7.2. Течение вязкой жидкости по трубам. Формула Пуазейля
- •Факторы, влияющие на вязкость крови в организме.
- •9.1. Модели кровообращения
- •Лекция 6
- •7.5. Турбулентное течение. Число Рейнольдса
- •9.1. Модели кровообращения
- •9.2. Пульсовая волна
- •9.3. Работа и мощность сердца. Аппарат искусственного кровообращения
- •Лекция 7.
- •Физические процессы в биологических мембранах
- •11.1. Строение и модели мембран
- •11.2. Некоторые физические свойства и параметры мембран
- •11.3. Перенос молекул (атомов) через мембраны. Уравнение Фика
- •11.4. Уравнение Нернста—Планка. Перенос ионов через мембраны
- •11.5. Разновидности пассивного переноса молекул и ионов через мембраны
- •11.6. Активный транспорт. Опыт Уссинга
- •Лекция 8.
- •11.7. Равновесный и стационарный мембранные потенциалы. Потенциал покоя
- •11.8. Потенциал действия и его распространение
- •11.9. Активно-возбудимые среды. Автоволновые процессы в сердечной мышце
- •Лекция 9.
- •Электрическое поле
- •12.1. Напряженность и потенциал — характеристики электрического поля
- •12.2. Электрический диполь
- •12.3. Понятие о мультиполе
- •12.4. Дипольный электрический генератор (токовый диполь)
- •12.5. Физические основы электрокардиографии
- •12.6. Диэлектрики в электрическом поле
- •12.7. Пьезоэлектрический эффект
- •12.8. Энергия электрического поля
- •12.11. Электрический разряд в газах. Аэроионы и их лечебно-профилактическое действие
- •Лекция 10.
- •12.9. Электропроводимость электролитов
- •12.10. Электропроводимость биологических тканей и жидкостей при постоянном токе
- •15.1. Первичное действие постоянного тока на ткани организма. Гальванизация. Электрофорез лекарственных веществ
- •14.2. Переменный ток
- •14.3. Полное сопротивление в цепи переменного тока. Резонанс напряжений
- •14.4. Импеданс тканей организма. Дисперсия импеданса. Физические основы реографии
- •Магнитное поле
- •13.1. Основные характеристики магнитного поля
- •13.2. Закон Ампера
- •13.3. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца
- •13.4. Магнитные свойства вещества
- •13.5. Магнитные свойства тканей организма. Понятие о биомагнетизме и магнитобиологии
12.7. Пьезоэлектрический эффект
В кристаллических диэлектриках поляризация может возникнуть и при отсутствии электрического поля из-за деформации.Это явление получило название пьезоэлектрического эффекта (пъезоэффекта).
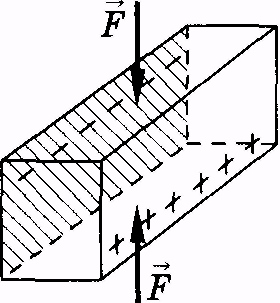
Различают поперечный (рис. 12.24) и продольный (рис. 12.25) пьезоэффекты. Стрелки показывают силы, действующие на кристалл. При изменении характера деформации, например, при переходе от сжатия к растяжению, изменится и знак возникающих поляризационных зарядов.
Пьезоэлектрический эффект обусловлен деформацией элементарных кристаллических ячеек и сдвигом подрешеток относительно друг друга при механических деформациях. Поляризован-ность при небольших механических деформациях пропорциональна их величине. Пьезоэффект возникает в кварце, сегнетовой соли и некоторых других кристаллах.



Для демонстрации пьезоэффекта можно использовать установку, схема которой изображена на рис. 12.26. К кристаллу К, обладающему пьезоэлектрическими свойствами, приложены металлические пластины М, которые замкнуты через неоновую лампу Н. Эта лампа потребляет небольшой силы ток и загорается при определенном напряжении, т. е. является своеобразным индикатором напряжения.
При ударе по кристаллу (деформации) появляется напряжение на его гранях, а значит, и на металлических пластинах, и неоновая лампа вспыхивает.
Наряду с рассмотренным прямым пьезоэлектрическим эффектом наблюдается и обратный пьезоэффект: при наложении электрического поля на кристаллы последние деформируются.
Оба пьезоэффекта — прямой и обратный — применяют в тех случаях, когда необходимо преобразовать механическую величину в электрическую или наоборот.
Так, прямой пьезоэффект используют в медицине — в датчиках для регистрации пульса, в технике — в адаптерах, микрофонах и для измерения вибраций, а обратный пьезоэффект — для создания механических колебаний и волн ультразвуковой частоты.
Существенный пъезоэффект возникает в костной ткани при наличии сдвиговых деформаций.
Причина эффекта — деформация коллагена — основного белка соединительной ткани. Поэтому пьезоэлектрическими свойствами обладают также сухожилия и кожа. При нормальной функциональной нагрузке, а также при отсутствии дефектов в строении кости в ней существуют только деформации сжатия — растяжения и пьезоэффект отсутствует. Когда что-то ненормально и возникает сдвиговая деформация, то возникает пьезоэффект. Он оказывает влияние на постоянно идущие в кости процессы разрушения и созидания и содействует тому, чтобы исчез сдвиг (меняется архитектура и даже форма кости). Указывают два возможных механизма воздействия пьезоэффекта: а) электрическое поле изменяет активность клеток, продуцирующих коллаген, и б) электрическое поле участвует в укладке макромолекул. Исследованием этого вопроса занимался В. Ф. Чепель.
12.8. Энергия электрического поля
Система зарядов или заряженных тел, заряженный конденсатор обладают энергией.
В этом можно убедиться, разряжая, например, конденсатор через лампочку, присоединенную к нему: лампочка вспыхнет.
Вычислим энергию поля конденсатора. Чтобы зарядить его, будем многократно переносить положительный заряд dq с одной обкладки на другую. По мере его переноса увеличивается напряжение между обкладками конденсатора. Работа, которую необходимо совершить против сил электрического поля для зарядки конденсатора, равна энергии конденсатора:
![]()
Элементарная работа по перемещению заряда против сил поля равна dA = Udq. Перенос заряда dq с одной обкладки конденсатора на другую изменяет напряжение его на dU, и тогда из формулы для электроемкости запишем dq = CdU, a значит, dA = CUdU.
Проинтегрировав это равенство в пределах от U0 = 0 до некоторого конечного значения U, найдем выражение для энергии поля заряженного конденсатора:
![]()
Е сли,
не изменяя заряда на обкладках
конденсатора,
отключенного от источника напряжения,
раздвинуть его пластины от расстояния
l1
до l2,
то электроемкость
уменьшится (см.
12.34). Как видно из (12.44), при этом
энергия конденсатора с увеличением
объема, занимаемого электрическим полем
(рис. 12.27), возрастет, а напряженность
поля останется постоянной. Отсюда ясно,
что энергия заряженного
конденсатора сосредоточена в объеме,
занимаемом электрическим полем.
сли,
не изменяя заряда на обкладках
конденсатора,
отключенного от источника напряжения,
раздвинуть его пластины от расстояния
l1
до l2,
то электроемкость
уменьшится (см.
12.34). Как видно из (12.44), при этом
энергия конденсатора с увеличением
объема, занимаемого электрическим полем
(рис. 12.27), возрастет, а напряженность
поля останется постоянной. Отсюда ясно,
что энергия заряженного
конденсатора сосредоточена в объеме,
занимаемом электрическим полем.
Более убедительно пояснить существование энергии электрического поля можно на примере переменного электромагнитного поля (передача сигнала на расстояние, давление света и т. п.).
Выразим энергию поля через его характеристики. С этой целью преобразуем (12.43), подставив выражение для емкости плоского конденсатора (12.34) и напряжение из (12.14):
![]() (12.45)
(12.45)
где V = SI — объем, занимаемый электрическим полем конденсатора.
Предполагая, что электрическое поле плоского конденсатора однородно, разделим (12.45) на объем и получим объемную плотность энергии поля:
![]() (12.46)
(12.46)
Единицей объемной плотности является джоуль на кубический метр (Дж/м3).
В заключение заметим, что формула (12.46) справедлива и для неоднородного электрического поля, но тогда она выражает объемную плотность энергии в точке. Энергия неоднородного поля может быть найдена интегрированием (12.46) по соответствующему объему
![]()
В общем случае диэлектрическая проницаемость различна в разных точках среды, т. е. зависит от координат, поэтому в этой формулевходит под знак интеграла.
