
- •Теория вероятностей
- •§2.1. Случайное событие. Вероятность
- •§ 2.2. Случайная величина. Закон распределения. Числовые характеристики
- •§ 2.3. Нормальный закон распределения
- •§ 2.4. Распределения Максвелла и Больцмана
- •Лекция 2.
- •Математическая статистика
- •§3.1. Основные понятия математической статистики
- •§ 3.2. Оценка параметров генеральной совокупности по ее выборке
- •§3.3. Проверка гипотез
- •§ 3.4. Корреляционная зависимость. Уравнения регрессии
- •Лекция 3.
- •Механические колебания и волны.
- •5.1. Свободные механические колебания (незатухающие и затухающие)
- •5.2. Кинетическая и потенциальная энергии колебательного движения
- •5.3. Сложение гармонических колебаний
- •5.4. Сложное колебание и его гармонический спектр
- •5.5. Вынужденные колебания. Резонанс
- •5.6. Автоколебания
- •5.7. Уравнение механической волны
- •5.8. Поток энергии и интенсивность волны
- •5.9. Ударные волны
- •5.10. Эффект Доплера
- •Лекция 4
- •Акустика
- •6.1. Природа звука и его физические характеристики
- •§ 6.2. Характеристики слухового ощущения. Понятие об аудиометрии.
- •§ 6.3. Физические основы звуковых методов исследования в клинике
- •§ 6.4. Волновое сопротивление. Отражение звуковых волн. Реверберация
- •§ 6.5. Физика слуха
- •6.6. Ультразвук и его применения в медицине
- •6.7. Инфразвук
- •6.8. Вибрации
- •Лекция 5
- •Течение и свойства жидкостей
- •Уравнение Бернулли.
- •1. Схема трубки тока жидкости для вывода формулы Бернулли.
- •1)Наклонная трубка тока постоянного сечения.
- •2)Горизонтальная трубка тока переменного сечения.
- •3) Измерение скорости жидкости. Трубка Пито.
- •7.1. Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости
- •7.2. Течение вязкой жидкости по трубам. Формула Пуазейля
- •Факторы, влияющие на вязкость крови в организме.
- •9.1. Модели кровообращения
- •Лекция 6
- •7.5. Турбулентное течение. Число Рейнольдса
- •9.1. Модели кровообращения
- •9.2. Пульсовая волна
- •9.3. Работа и мощность сердца. Аппарат искусственного кровообращения
- •Лекция 7.
- •Физические процессы в биологических мембранах
- •11.1. Строение и модели мембран
- •11.2. Некоторые физические свойства и параметры мембран
- •11.3. Перенос молекул (атомов) через мембраны. Уравнение Фика
- •11.4. Уравнение Нернста—Планка. Перенос ионов через мембраны
- •11.5. Разновидности пассивного переноса молекул и ионов через мембраны
- •11.6. Активный транспорт. Опыт Уссинга
- •Лекция 8.
- •11.7. Равновесный и стационарный мембранные потенциалы. Потенциал покоя
- •11.8. Потенциал действия и его распространение
- •11.9. Активно-возбудимые среды. Автоволновые процессы в сердечной мышце
- •Лекция 9.
- •Электрическое поле
- •12.1. Напряженность и потенциал — характеристики электрического поля
- •12.2. Электрический диполь
- •12.3. Понятие о мультиполе
- •12.4. Дипольный электрический генератор (токовый диполь)
- •12.5. Физические основы электрокардиографии
- •12.6. Диэлектрики в электрическом поле
- •12.7. Пьезоэлектрический эффект
- •12.8. Энергия электрического поля
- •12.11. Электрический разряд в газах. Аэроионы и их лечебно-профилактическое действие
- •Лекция 10.
- •12.9. Электропроводимость электролитов
- •12.10. Электропроводимость биологических тканей и жидкостей при постоянном токе
- •15.1. Первичное действие постоянного тока на ткани организма. Гальванизация. Электрофорез лекарственных веществ
- •14.2. Переменный ток
- •14.3. Полное сопротивление в цепи переменного тока. Резонанс напряжений
- •14.4. Импеданс тканей организма. Дисперсия импеданса. Физические основы реографии
- •Магнитное поле
- •13.1. Основные характеристики магнитного поля
- •13.2. Закон Ампера
- •13.3. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца
- •13.4. Магнитные свойства вещества
- •13.5. Магнитные свойства тканей организма. Понятие о биомагнетизме и магнитобиологии
12.6. Диэлектрики в электрическом поле
Диэлектриками называют тела, не проводящие электрического тока.
Термин «диэлектрик» введен М. Фарадеем для обозначения веществ, через которые проникают электрические поля, в отличие от металлов, внутри которых электростатического поля нет. К диэлектрикам относят твердые тела, такие, как эбонит, фарфор, а также жидкости (например, чистая вода) и газы.
При изменении внешних условий (нагревание, воздействие ионизирующих излучений и т. п.) диэлектрик может проводитьэлектрический ток. Изменение состояния диэлектрика при помещении в электрическое поле можно объяснить его молекулярнымстроением. Условно выделим три класса диэлектриков: 1) полярные; 2) неполярные; 3) кристаллические.
К первому классу принадлежат такие вещества, как вода, нитробензол и др. Молекулы этих диэлектриков не симметричны, «центры масс» их положительных и отрицательных зарядов не совпадают, поэтому такие молекулы обладают электрическим дипольным моментом даже в случае, когда электрического поля нет.
На рис. 12.19 схематически показаны молекулы соляной кислоты (а) и воды (б) и соответствующие им дипольные моменты в дебаях1.(1 Дебай (Д) — внесистемная единица дипольного момента молекул: 1Д = 3,33564 • 10-30Кл • м.)

В отсутствие электрического поля
дипольные моменты молекул
ориентированы хаотически (рис. 12.20, а) и
векторная сумма моментов всех N
молекул равна
нулю:
![]()
Если диэлектрик
поместить в электрическое поле, то
дипольные моменты
молекул стремятся ориентироваться
вдоль поля (рис.
12.20, б), однако
полной ориентации не будет вследствие
молекулярно-теплового хаотического
движения. В этом случае
![]()
Ко второму классу
диэлектриков относят такие вещества
(например,
водород, кислород и др.), молекулы которых
в отсутствие электрического
поля не имеют дипольных моментов. В
таких молекулах заряды электронов
и ядер расположены так, что «центры
масс» положительных и отрицательных
зарядов совпадают. Если неполярную
молекулу поместить в электрическое
поле, то разноименные заряды несколько
сместятся в противоположные стороны
и молекула будет иметь дипольный момент.
На рис. 12.21 схематически
в виде кружков показаны молекулы такого
диэлектрика
в отсутствие поля
![]() (а)
и при наложении
поля
(а)
и при наложении
поля
![]() (б)(стрелки
у кружков означают дипольные моменты
молекул).
(б)(стрелки
у кружков означают дипольные моменты
молекул).

Третий класс — кристаллические диэлектрики (например, NaCl), решетка которых состоит из положительных и отрицательных ионов. Такой диэлектрик можно схематически рассматривать как совокупность двух «подрешеток», одна из которых заряжена положительно, другая — отрицательно. При отсутствии поля подрешетки расположены симметрично и суммарный электрический момент такого диэлектрика равен нулю1. (1 Строго говоря, ионные кристаллы могут обладать электрическим моментом и при отсутствии внешнего поля, однако здесь это не учтено.)Если диэлектрик поместить в электрическое поле, то подрешетки немного сместятся в противоположные стороны и диэлектрик приобретет электрический момент.
Все эти процессы, происходящие в разных диэлектриках при наложении электрического поля, объединяют общим термином поляризация, т. е. приобретение диэлектриком дипольного момента.
Для первого класса диэлектриков характерна ориентационная поляризация, для второго — электронная, т. е. смещение главным образом электронных оболочек, для третьего — ионная. Такая классификация условна, так как в реальном диэлектрике могут одновременно существовать все виды поляризации.
Изменение напряженности
электрического поля, в котором находится
диэлектрик, будет влиять на состояние
его поляризации. Охарактеризовать
степень поляризации диэлектрика
суммарным электрическим моментом всех
его N молекул
 нельзя, так как
эта величина зависит, в частности, от
объема диэлектрика.Для
оценки состояния поляризации диэлектрика
вводят величину,
называемую поляризованностъю,
среднее
значение которой равно отношению
суммарного электрического момента
элемента объема V
диэлектрика
к этому объему:
нельзя, так как
эта величина зависит, в частности, от
объема диэлектрика.Для
оценки состояния поляризации диэлектрика
вводят величину,
называемую поляризованностъю,
среднее
значение которой равно отношению
суммарного электрического момента
элемента объема V
диэлектрика
к этому объему:
![]() (12.36)
(12.36)
Единицей поляризованности является кулон на квадратный метр (Кл/м2).
При поляризации диэлектрика на одной его поверхности (грани) создаются положительные заряды, а на другой — отрицательные (см. рис. 12.20, б и 12.21, б). Эти электрические заряды называют связанными, так как они принадлежат молекулам диэлектрика (или кристаллической решетке при ионной поляризации) и не могут перемещаться в отрыве от молекул или быть удалены с поверхности диэлектрика в отличие от свободных зарядов, которых в идеальном диэлектрике нет.
При возрастании напряженности электрического поля растет степень упорядоченности ориентации молекул (ориентационная поляризация), увеличиваются дипольные моменты молекул (электронная поляризация), а также происходит большее смещение «подрешеток» (ионная поляризация) — все это приводит к увеличению поверхностной плотности св связанных электрических зарядов.
Таким образом, св также характеризует степень поляризации диэлектрика.
Установим связь между Ре и св на примере поляризованного диэлектрика, имеющего форму параллелепипеда (рис. 12.22, а). Такой параллелепипед представим как совокупность диполей, которые, простоты ради,можно рассматривать как «цепочки»; одна из них показана на рис. 12.22, б. Так как внутренние части «цепочки» диполей электрически компенсируются, то такая «цепочка» подобна длинному диполю с расстоянием между зарядами, равным ребру параллелепипеда.

Если на грани
параллелепипеда с площадью S
возник связанный заряд
</ов,
то суммарный электрический момент![]() всего
параллелепипеда
численно равен дсв
/, но так как
всего
параллелепипеда
численно равен дсв
/, но так как
![]() Объем
параллелепипедаV
= SI cos. На основании двух
последних равенств имеем
Объем
параллелепипедаV
= SI cos. На основании двух
последних равенств имеем
![]() (12.37)
(12.37)
Учитывая (12.36) и (12.37), получаем
![]()
откуда
![]()
Итак, поверхностная плотность связанных зарядов св равна нормальной к грани составляющей вектора Ре.
Р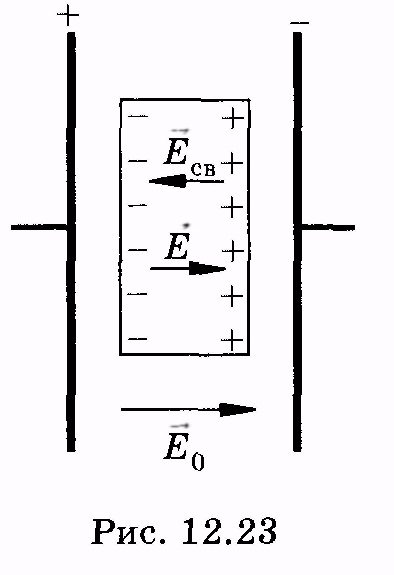 ассмотрим,
например, плоский диэлектрик, расположенныйв однородном
электрическом поле (рис. 12.23);
ассмотрим,
например, плоский диэлектрик, расположенныйв однородном
электрическом поле (рис. 12.23);
![]() — напряженность
поля в отсутствие диэлектрика (поле в
вакууме). Связанные заряды
создают однородное поле напряженностью
— напряженность
поля в отсутствие диэлектрика (поле в
вакууме). Связанные заряды
создают однородное поле напряженностью
![]() ,
в результате
в диэлектрике будет электрическое поле
напряженностью
,
в результате
в диэлектрике будет электрическое поле
напряженностью
Е = Е0 - Есв (12.39)
Известно, что диэлектрическая проницаемость средыравна отношению силы взаимодействия зарядов в вакууме к силе взаимодействия этих же зарядов на том же расстоянии в среде:
F0/F = , или F0 = F.
Так как напряженность электрического поля пропорциональна силе, действующей на заряд [см. (12.1)], то аналогичное соотношение можно записать для Е0 и Е:
Е0 = Е. (12.40)
Напряженность электрического поля, образованного связанными электрическими зарядами, Есв = св/0. Для данного примера из (12.38) имеем св = Ре, тогда Есв = Ре/0. Подставляя эту формулу и (12.40) в (12.39), получаем Е = Е - Ре/0, или Е(0 - 1) = =Ре/0, откуда
Ре = 0(- 1)Е. (12.41)
Как и можно было ожидать, поляризованность пропорциональна напряженности электрического поля в диэлектрике. На основании (12.41) вводят понятие диэлектрической восприимчивости среды
= -1,(12-42)
которая вместе с диэлектрической проницаемостью характеризует способность диэлектрика к поляризации и зависит от его молекулярного строения, а возможно и от температуры. В переменных электрических полях и изменяются также в зависимости от частоты.
В табл. 21 приведены значения диэлектрической проницаемости для различных биологических сред и некоторых веществ в постоянном электрическом поле при комнатной температуре.
Таблица 21
|
|
|
|
|
|
|
Керосин |
2 |
|
Белок яичный |
72 |
|
Масло растительное |
2—4 |
|
Вода |
81 |
|
Стекло |
6—10 |
|
Кровь цельная |
85 |
|
Крахмал |
12 |
|
Серое вещество мозга |
85 |
|
Молоко коровье |
66 |
|
Нерв зрительный |
89 |
|
|
|
|
Белое вещество мозга |
90 |
Различие диэлектрической проницаемости нормальных и патологических тканей и сред как в постоянных, так и в переменных, электрических полях можно использовать для диагностических целей.
