11.8. Потенциал действия и его распространение

Все живые клетки при действии различных раздражителей (химических, механических, температурных и пр.) способны переходить в возбужденное состояние. Опыт показывает, что возбужденный участок становится электроотрицательным по отношению к покоящемуся, что является показателем перераспределения ионных потоков в возбужденном участке. Реверсия потенциала при возбуждении кратковременна, и после окончания возбуждения через некоторое время вновь восстанавливается исходный потенциал покоя. Общее изменение разности потенциалов на мембране, происходящее при возбуждении клеток, называется потенциалом действия. На рис. 11.17 представлен потенциал действия гигантского аксона кальмара, обозначены отдельные стадии изменения потенциала. В частности, для клетки характерен так называемый запаздывающий потенциал, когда в течение некоторого времени на мембране существует даже меньший потенциал, чем потенциал покоя.

Было показано, что возбуждение связано с увеличением электропроводности клеточной мембраны. При этом временная зависимость электропроводимости повторяла форму потенциала действия. Чтобы решить вопрос, для каких ионов изменяется проницаемость мембраны, следует обратить внимание, что потенциал действия приводит к кратковременному возрастанию потенциала внутри клетки (см. рис. 11.17). Отрицательный относительно внешней среды потенциал становится положительным. Если по уравнению Нернста (11.38) вычислить равновесные потенциалы на мембране аксона кальмара, то получим соответственно для ионов К+, Na+ и Сl^-величины -90, +46 и -29 мВ. Так как при изменении проницаемости мембраны для какого-либо иона этот ион будет проникать через нее, стремясь создать равновесное состояние, то числовые данные показывают, что внутрь клетки проникают ионы Na+, создавая там положительный потенциал. Следовательно, при возбуждении клетки в начальный период увеличивается проницаемость мембран именно для ионов натрия. «Натриевая теория» возникновения потенциала действия была предложена, разработана и экспериментально подтверждена А. Ходжкином и А. Хаксли, за что в 1963 г. они были удостоены Нобелевской премии.

Измерить проницаемость мембран для какого-либо иона (иначе говоря, электропроводимость или сопротивление мембраны для этого иона) можно, если на основании закона Ома найти отношение тока к напряжению, или наоборот. Практическая реализация такой задачи осложняется тем, что проницаемость (электрическое сопротивление) мембраны при возбуждении изменяется со временем. Это приводит к перераспределению электрического напряжения в цепи, и разность потенциалов на мембране изменяется. Ходжкин, Хаксли и Катц смогли создать опыт с фиксацией определенного значения разности потенциала на мембране. Это позволило им провести измерение ионных токов и, следовательно, проницаемости (сопротивления) мембран для ионов. Оказалось, что отношение проницаемостей мембраны для ионов натрия и калия практически повторяет форму потенциала действия. Кроме того, были получены кривые временной зависимости ионных токов через мембрану (рис. 11.18). На этом рисунке кривая1соответствует временной зависимости суммарного ионного тока через мембрану гигантского аксона кальмара, полученного при изменении потенциала на мембране до +56 мВ (потенциал покоя равен60 мВ). Вначале направление тока отрицательно, что соответствует прохождению положительных ионов через мембрану клетки. Было установлено, что ток этот обусловлен прохождением ионов натрия внутрь клетки, где концентрация их значительно меньше, чем снаружи.

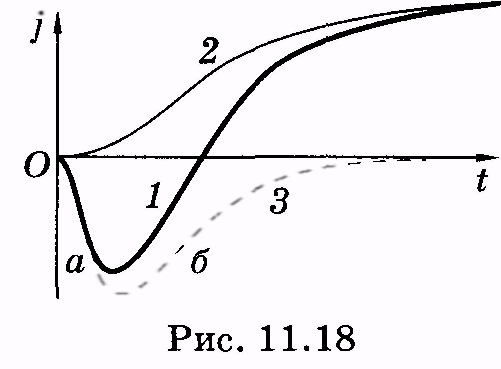
Естественно, что при таком нарушении равновесия ионы калия начнут перемещаться наружу, где их концентрация существенно меньше. Для того чтобы выяснить, какая часть тока «натриевая», а какая «калиевая», можно провести то же возбуждение, но в искусственных условиях, когда в среде, окружающей аксон, нет натрия. В этом случае (см. кривую 2) ток обусловливается только выходом ионов калия наружу из клетки. Разница значений тока для двух кривых показана на кривой3: кривая3есть разность кривых1и2. Она дает зависимость от времени ионного тока натрия. На этой кривой частьасоответствует открыванию натриевых каналов, аб— их закрытию (инактивации).

В целом последовательность событий, происходящих на клеточной мембране при возбуждении, выглядит следующим образом. При возбуждении в мембране открываются каналы для ионов натрия (проницаемость мембраны возрастает более чем в 5000 раз). В результате отрицательный заряд с внутренней стороны мембраны становится положительным, что соответствует пику мембранного потенциала (фаза деполяризации мембраны). Затем поступление натрия из внешней среды прекращается. В это время натриевые каналы закрываются, но открываются калиевые. Калий проходит в соответствии с градиентом концентрации из клетки до тех пор, пока не восстановится первоначальный отрицательный заряд на мембране и мембранный потенциал не достигнет своего первоначального значения (фаза реполяризации). На самом деле выход ионов калия из клетки продолжается дольше, чем это требуется для восстановления потенциала покоя. В результате за пиком потенциала действия следует небольшой минимум (за­паздывающий потенциал).

Ионные каналы имеют белковое происхождение (см. рис. 11.3 и 11.13). Они селективно (выборочно) пропускают ионы разного вида. Канал может быть «закрыт» (блокирован) молекулами ядов, его пропускная способность зависит от действия некоторых лекарственных средств. Поэтому теория ионных каналов в мембранах является важной частью молекулярной фармакологии.

Механизм распространения потенциала действия в деталях рассматривается в курсе нормальной физиологии. Мы же рассмотрим лишь некоторые основные положения. Распространение потенциала действия вдоль нервного волокна (аксона) обусловлено возникновением так называемыхлокальных токов, образующихся между возбужденным и невозбужденным уча­стками клетки. На рис. 11.19 схематично указаны отдельные стадии возникновения и распростране­ния потенциала действия. В состоянии покоя (рис. 11.19, а) внешняя поверхность клеточной мембраны имеет положительный потенциал, а внутренняя — отрицательный. В момент возбуждения полярность мембраны меняется на противоположную (рис. 11.19,б). В результате этого между возбужденным и невозбужденным участками мембраны возникает разность потенциалов. Наличие разности потенциалов и приводит к появлению между этими участкамилокальных токов. На поверхности клетки локальный ток течет от невозбужденного участка к возбужденному; внутри клетки он течет в обратном направлении (рис. 11.19, в). Локальный ток, как и любой электрический ток, раздражает соседние невозбужденные участки и вызывает увеличение проницаемости мембраны. Это приводит к возникновению потенциалов действия в соседних участках. В то же время в ранее возбужденном участке происходят восстановитель­ные процессы реполяризации. Вновь возбужденный участок в свою очередь становится электроотрицательным и возникающий ло­кальный ток раздражает следующий за ним участок. Этот процесс многократно повторяется и обусловливает распространение им­пульсов возбуждения по всей длине клетки в обоих направлениях (рис. 11.19,г). В нервной системе импульсы проходят лишь в опре­деленном направлении из-за наличия синапсов, обладающих односторонней проводимостью.

По электрическим свойствам аксон напоминает кабель с проводящей сердцевиной и изолирующей оболочкой. Однако для того чтобы в кабеле не было значительных потерь энергии при протекании тока, сопротивление его должно быть малым, а сопротивление изоляции — очень большим. В аксоне проводящим веществом служит аксоплазма, т. е. раствор электролита, удельноесопротивление которого в миллионыраз больше, чем у меди или алюми­ния, из которых изготавливают обычные кабели. Удельное сопротивление биомембран достаточно велико, но вследствие их малой толщины сопротивление изоляции «аксонного кабеля» в сотни тысяч раз меньше, чем у технического кабеля. По этой причине однородное нервное волокно не может проводить электрический сигнал на далекое расстояние, интенсивность сигнала быстро затухает. Расчеты показывают, что напряжение на мембране волокна будет экспоненциально уменьшаться по мере удаления от места возбуждения (рис. 11.20). Если величина потенциала действия в месте возбуждения была равна _mах, то на расстоянии l от этого места потенциал на мембране будет равен:

(11.40)

где — постоянная длины нервного волокна, которая определяет степень затухания сигнала в аксоне по экспоненциальному закону. Эту величину можно рассчитать по следующей приближеннойформуле:

(11.41)

где d — диаметр волокна, R — поверхностное сопротивление мембраны в Ом • м² (т. е. сопротивление 1 м² ее поверхности) и  — удельное сопротивление аксоплазмы в Ом • м.

Расчеты, проведенные для аксона кальмара, показывают, что на конце аксона величина сигнала должна быть ничтожно малой. Однако существование локальных токов приводит к тому, что возбуждение передается по нервному волокну без затухания. Это объясняется тем, что локальные токи лишь деполяризуют мембрану до критического уровня, а потенциалы действия в каждом участке мембраны поддерживаются независимыми ионными потоками, перпендикулярными к направлению распространения возбуждения.

Из (11.40) видно, что с увеличением  степень затухания сигнала уменьшается. Было показано, что при этом возрастает скорость проведения импульса, а это очень важно для жизнедеятельности любого организма. Величины  и  примерно одинаковы для всех животных клеток, и поэтому увеличения постоянной длины  можно добиться путем увеличения диаметра d аксона. Именно поэтому у кальмаров аксоны достигают «гигантских» размеров (диаметр до 0,5 мм), что обеспечивает кальмару достаточно быстрое проведение нервного импульса и, следовательно, быстроту реакции на внешние раздражители.

Увысокоорганизованных животных с развитой нервной системой толстые волокна оказываются неэкономичными, и затухание сигнала предотвращается другим способом. Мембраны аксонов у них покрытымиелином — веществом, содержащим много холестерина и мало белка (рис. 11.21). Удельное сопротивление миелина значительно выше удельного сопротивления других биологических мембран. Помимо этого, толщина миелиновой оболочки во много раз больше толщины обычной мембраны, что приводит к возрастанию диаметра волокна и соответственно величины. Как видно из рис. 11.21, миелиновая оболочка не полностью покрывает все волокно; оно разделено на отдельные сегменты, между которыми на участках длиной около 1 мкм мембрана аксона непосредственно соприкасается с внеклеточным раствором. Области, вкоторых мембрана контактирует с раствором, называют перехва­тами Ранвье. В связи с большим сопротивлением миелиновой оболочки по поверхности аксона токи протекать не могут, и затухание сигнала резко уменьшается. При возбуждении одного узла возникают токи между ним и другими узлами. Ток, подошедший к другому узлу, возбуждает его, вызывает появление в этом местепотенциала действия, и процесс распространяется по всему во­локну. Затраты энергии на распространение сигнала по волокну,покрытому миелином, значительно меньше, чем по немиелинизированному, так как общее количество ионов натрия, проходящих через мембрану в области узлов, значительно меньше, чем если бы они проходили через всю поверхность мембраны. При некоторых заболеваниях структура миелиновых оболочек нарушается, и это приводит к нарушению проведения нервного возбуждения. При блокировании узлов нервного волокна анестезирующими средствами, например ядом кураре, сопротивление аксона возрастает и прохождение сигналов по нерву замедляется или совсемпрекращается.

Поскольку узлы замыкаются через аксоплазму и внеклеточную среду, то можно предположить, что при увеличении сопротивления внешней среды скорость проведения нервного импульса уменьшится. Это предположение было проверено на опыте. Нервные волокна сначала помещали в морскую воду, а затем в масло с большим удельным сопротивлением. Скорость проведения им­пульса во втором случае уменьшалась в 1,5—2 раза (в зависимости от диаметра волокна).

Существует некоторая формальная аналогия между распространением потенциала действия по нервному волокну и электромагнитной волной в двухпроводной линии или коаксиальном кабеле. Однако между этими процессами имеется существенное различие.Электромагнитная волна, распространяясь в среде, ослабевает, так как растрачивает свою энергию. Волна возбуждения, прохо­дящая по нервному волокну, не затухает, получая энергию в са­мой среде (энергию заряженной мембраны). Волны, получающие энергию из среды в процессе распространения, называютавтоволнами, а среду — активно-возбудимой средой (ABC). В § 11.9 будут рассмотрены более подробно свойства авто волн, распростра­няющихся в ABC.