9.1. Модели кровообращения

Рассмотрим гидродинамическую модель кровеносной системы,предложенную О. Франком. Несмотря на достаточную простоту, она позволяет установить связь между ударным объемом крови (объем крови, выбрасываемый желу­дочком сердца за одну систолу), гид­равлическим сопротивлением перифе­рической части системы кровообраще­ния Х₀ и изменением давления в артериях. Артериальная часть систе­мы кровообращения моделируется уп­ругим (эластичным) резервуаром (рис. 9.1, обозначено УР).

Так как кровь находится в упругом резервуаре, то ее объем V влюбой момент времени зависит от давления р по следующему со­отношению:

V = V₀ + kp, (9.1)

где k — эластичность, упругость резервуара (коэффициент про­порциональности между давлением и объемом), V₀ — объем ре­зервуара при отсутствии давления(р = 0). Продифференцировав(9.1), получим

(9.2)

В упругий резервуар (артерии) поступает кровь из сердца, объемная скорость кровотока равна Q. От упругого резервуара кровь оттекает с объемной скоростью кровотока Q₀ в периферическук систему (артериолы, капилляры). Предполагаем, что гидравлическое сопротивление периферической системы постоянно. Это моделируется «жесткой» трубкой на выходе упругого резервуара (рис. 9.1).

Можно составить достаточно очевидное уравнение (рис. 9.1)

(9.3)

показывающее, что объемная скорость кровотока из сердца равна сумме скорости возрастания объема упругого резервуара и скорос­ти оттока крови из упругого резервуара.

На основании уравнения Пуазейля (7.8) и формулы (7.9) мож­но записать для периферической части системы

(9.4)

где р — давление в упругом резервуаре, р_в — венозное давление, оно может быть принято равным нулю, тогда вместо (9.4) имеем

(9.5)

Подставляя (9.2) и (9.5) в (9.3), получаем

или(9.6)

Проинтегрируем (9.6). Пределы интегрирования по времени соот­ветствуют периоду пульса (периоду сокращения сердца) от 0 до Т_п. Этим временным пределам соответствуют одинаковые давления — минимальное диастолическое давлениер_д:

(9.7)

Интеграл с равными пределами равен нулю, поэтому из (9.7) имеем

(9.8)

Экспериментальная кривая, показывающая временную зависи­мость давления в сонной артерии, приведена на рис. 9.2 (сплошнаялиния). На рисунке показан период пульса, длительности Т_с сис­толы и Т_д диастолы, р_с — максимальное (систолическое) давление. Интеграл в левой части уравнения (9.8) равен объему крови, который выталкивается из сердца за одно сокращение, — удар­ный объем. Он может быть найден экспериментально. Интеграл в правой части уравнения (9.8) соответствует площади фигуры, ог­раниченной кривой и осью времени (см. рис. 9.2), что также мож­но найти. Используя указанные значения интегралов, можно вы­числить по (9.8) гидравлическое сопротивление периферической части системы кровообращения.

Во время систолы (сокращение сердца) происходит расширение упругогорезервуара, после систолы, во время ди­астолы — отток крови к периферии, Q = 0. Для этого периода из (9.6) имеем

или(9.9)

Проинтегрировав (9.9), получаем за­висимость давления в резервуаре пос­ле систолы от времени:

(9.10)

Соответствующая кривая изображена тонкой линией на рис. 9.2. На основании (9.5) получаем зависимость объемной скоростиоттока крови от времени:

(9.11)

где — объемная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).

Зависимости (9.10) и (9.11) представляют собой экспоненты. Хотя данная модель весьма грубо описывает реальное явление, она чрезвычайно проста и верно отражает процесс к концу диасто­лы. Вместе с тем изменения давления в начале диастолы с по­мощью этой модели не описываются.

На основе механической модели по аналогии может быть по­строена электрическая модель (рис. 9.3).

Здесь источник U, дающий несинусоидальное переменное элект­рическое напряжение, служит аналогом сердца, выпрямительВ — сердечного клапана. Конденсатор С в течение полупериода накап­ливает заряд, а затем разряжается на резистор R, таким образом происходит сглаживание силы тока, протекающего через резистор. Действие конденсатора аналогично действию упругого резервуара (аорты, артерии), который сглаживает колебание давления крови вартериолах и капиллярах. Резистор является электрическим ана­логом периферической сосудистой системы.

В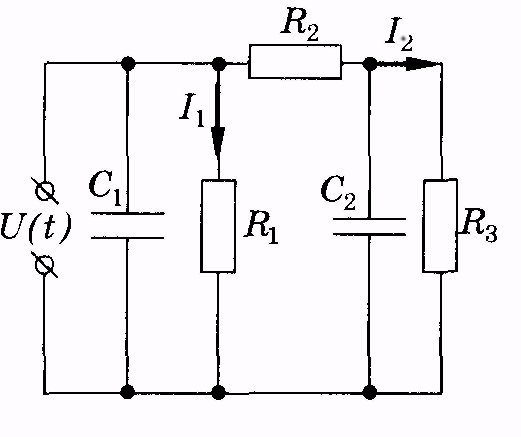более точной модели сосудистого русла использовалось боль­шее количество эластичных резервуаров для учета того факта, что сосудистое русло является системой, распределенной в простран­стве. Для учета инерционных свойств крови при построении моде­ли предполагалось, что эластичные резервуары, моделирующие восходящую и нисходящую ветви аорты, обладают различной уп­ругостью. На рис. 9.4 приведено изображение модели Ростона, со­стоящей из двух резервуаров с различными эластичностями (упругостями) и с неупругими звеньями разного гидравлического сопротивления между резервуарами. Этой модели соответствует электрическая схема, изображенная на рис. 9.5. Здесь источник тока задает пульси­рующее напряжение U(t), являющее­ся аналогом давленияp(t); емкостиС₁

и С₂ соответствуют упругостям резер­вуаров k₁ и k₂, электрические сопро­тивления R_v R₂ и R₃ — гидравличе­ским сопротивлениямX_lf X₂ иХ₃, си­лы тока /j и /₂ — объемным скоростям оттока крови Q₁ и Q₂.

Такая модель математически описывается системой двух диф­ференциальных уравнений первого порядка, их решение дает

Рис. 9.5 две кривые, соответствующие первой и второй камерам.

Двухкамерная модель лучше описывает процессы, происходя­щие в сосудистом русле, но и она не объясняет колебания давле­ния в начале диастолы.

Модели, содержащие несколько сотен элементов, называют мо­делями с распределенными параметрами.