Глава 8. Расчет оболочек составных и со шпангоутами простейшим методом «сопряжения участков интервала интегрирования».
8.1. Вариант записи метода решения жестких краевых задач без ортонормирования – метода «сопряжения участков, выраженных матричными экспонентами» - через положительные направления формул матричного интегрирования дифференциальных уравнений.
Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), включая края:
.
Имеем краевые условия в виде:
Можем записать матричные уравнения сопряжения участков:
,
,
.
Это мы можем переписать в виде, более удобном для нас далее:
,
,
.
где
- единичная матрица.
В итоге получаем систему линейных алгебраических уравнений:
.
Эта система решается методом Гаусса с выделением главного элемента.
Оказывается, что применять ортонормирование не нужно, так как участки интервала интегрирования выбираются такой длинны, что счет на них является устойчивым.
В точках вблизи узлов решение находится путем решения соответствующих задач Коши с началом в i-ом узле:
.
8.2. Составные оболочки вращения.
Рассмотрим сопряжения участков составной оболочки вращения.
Пусть имеем 3 участка, где каждый участок может выражаться своими дифференциальными уравнениями и физические параметры могут выражаться по-разному – разными формулами на разных участках:
В общем случае (на примере участка 12)
физические параметры участка (вектор
)
выражаются через искомые параметры
системы обыкновенных дифференциальных
уравнений этого участка (через вектор
)
следующим образом:
,
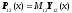где матрица
- квадратная невырожденная.
При переходе точки сопряжения можем
записать в общем виде (но на примере
точки сопряжения
):
,
где
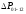- дискретное приращение физических
параметров (сил, моментов) при переходе
с участка «01» на участок «12», а матрица
квадратная невырожденная диагональная
и состоит из единиц и минус единиц на
главной диагонали для установления
правильного соответствия принятыхположительныхнаправленийсил,
моментов, перемещений и углов при
переходе с участка «01» на участок «12»,
которые могут быть разными (в разных
дифференциальных уравнениях разных
сопрягаемых участков) – в уравнениях
слева от точки сопряжения и в уравнениях
справа от точки сопряжения.
Два последних уравнения при объединении образуют уравнение:
.
В точке
сопряжения
аналогично получим уравнение:
.
Если бы оболочка состояла бы из одинаковых участков, то мы могли бы записать в объединенном матричном виде систему линейных алгебраических уравнений в следующей форме:
.
Но в нашем случае оболочка состоит из 3 участков, где средний участок можно считать, например, шпангоутом, выражаемым через свои дифференциальные уравнения.
Тогда вместо
векторов
,
,
,
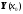мы
должны рассмотреть вектора:
.
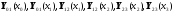Тогда матричные уравнения
,
,
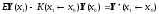примут вид:
,
,
,
,
.
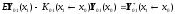После перестановки слагаемых получаем:
,
,
,
,
.
В итоге мы можем записать итоговую систему линейных алгебраических уравнений:
Эта система решается методом Гаусса с выделением главного элемента.
В точках, расположенных между узлами, решение находиться при помощи решения задач Коши с начальными условиями в i-ом узле:
.
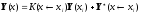Применять ортонормирование для краевых задач для жестких обыкновенных дифференциальных уравнений оказывается не надо.