
РГР 2
.docx-
Определение вектора, длины вектора
Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Длина-направленного отрезка определяет числовое значение вектора и называется длиной вектора
-
Определение Нулевого вектора
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
-
Определение ортов
Ортом или единичным
вектором  называется вектор, модуль которого
равен единице.
называется вектор, модуль которого
равен единице.
-
Определение компланарных и коллинеарных векторов
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
-
Определение суммы векторов
сумма
векторов а+b
есть операция вычисления вектора c
, все элементы которого равны попарной
сумме соответствующих элементов
векторов a
и b
, то есть каждый элемент вектора c
равен:
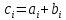
-
определение разности векторов
разность векторов a-b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

-
Определение проекции вектора на ось
Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l
Проекцией вектора a на направление вектора b, называется число, равное величине проекции вектора a на ось проходящую через вектор b.
-
Определение разложения вектора по ортам
Система ортов (или базисная система векторов) - это система единичных векторов осей координат.
Для
любого вектора ![]() ,
который лежит в плоскости
,
который лежит в плоскости ![]() ,
имеет место следующее разложение:
,
имеет место следующее разложение:![]()
Если
вектор ![]() расположен
в пространстве, то разложение по ортам
координатных осей имеет вид:
расположен
в пространстве, то разложение по ортам
координатных осей имеет вид: ![]()
-
Длина вектора в координатной форме
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB
-
Сумма и разность векторов в координатной форме
Сумма и разность векторов для плоских задач a = {ax ; ay} и b = {bx ; by}
a + b = {ax + bx; ay + by}
a - b = {ax - bx; ay - by}
Сумма и разность векторов для пространственных задач a = {ax ; ay ; az} и b = {bx ; by ; bz}
a + b = {ax + bx; ay + by; az + bz}
a - b = {ax - bx; ay - by; az - bz}
-
равенство векторов в координатной форме
Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении.
-
Коллинеарность векторов в координатной форме
-
Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
-
Два вектора коллинеарны, если отношения их координат равны
-
Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
|
a × b= |
i (aynaz - aznay) - j (axnaz - aznax) + k (axnay - aynax) = 0i + 0j + 0k = 0
-
определение радиус-вектора точки
радиус-вектором r точки М называется вектор, соединяющий начало координат О с этой точкой.
-
Опр. Скалярного произведения векторов.
Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
-
Вычисление скалярного произведения в координатной форме
a = {ax ; ay ; az} и b = {bx ; by ; bz}= а · b = ax · bx + ay · by + az · bz
-
условия перпендикулярности двух векторов в векторной и координатной форме
Два ненулевых вектора называются перпендикулярными, если угол между ними равен 90° градусам
-
Формула вычисления угла между двумя векторами
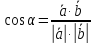
-
Определения векторного произведения векторов
Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов
-
Вычисление векторного произведения в координатной форме
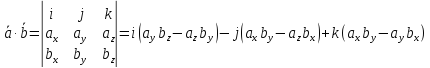
-
Геометрический смысл векторного произведения
модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах
-
Определения смешанного произведения векторов
Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c
-
Вычисление Смешанного произведения в координатной форме
a =
{ax; ay; az}, b =
{bx; by; bz}
и c =
{cx; cy; cz}
в декартовой системе координат можно
вычислить, используя следующую формулу:
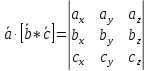
-
Геометрический смысл смешанного произведения
если тройка
векторов ![]() правая,
то их смешанное произведение равно
объему параллелепипеда построенного
на этих векторах:
правая,
то их смешанное произведение равно
объему параллелепипеда построенного
на этих векторах: ![]() .
В случае левой тройки
.
В случае левой тройки ![]() смешанное
произведение указанных векторов равно
объему параллелепипеда со знаком
минус:
смешанное
произведение указанных векторов равно
объему параллелепипеда со знаком
минус: ![]() .
Если
.
Если ![]() ,
, ![]() и
и ![]() компланарны, то их смешанное произведение
равно нулю.
компланарны, то их смешанное произведение
равно нулю.
-
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
A(x − x0) + B(y − y0) + C(z − z0) = 0
-
Общее уравнение плоскости
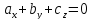
-
Какой геометрический смысл имеют коэффициенты в общем уравнении плоскости?
-
Частные случаи общего уравнения плоскости.
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат;
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
-
Уравнения плоскости проходящей через три данные точки
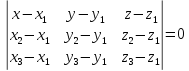
-
Угол между двумя плоскостями
угол между плоскостями равен углу образованному прямыми лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
-
Условия параллельности и перпендикулярности двух плоскостей
-
В случае перпендикулярности двух плоскостей

Угол между ними 90°(cos a=0)
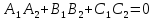
-
В случае параллельности плоскостей
параллельны
тогда и только тогда, когда их нормальные
векторы ![]() и
и ![]() параллельны:
параллельны:
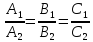
-
Расстояние от точки до плоскости
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
-
Канонические уравнения прямой
Каноническим
уравнением прямой, проходящей через
данную точку ![]() и
имеющей заданный направляющий
вектор
и
имеющей заданный направляющий
вектор ![]() ,
называется уравнение вида
,
называется уравнение вида
![]() .
.
-
Какой геометрический смысл имеют коэффициенты, входящие в канонические уравнения прямой?
-
Уравнения прямой в пространстве, проходящей через две заданные точки.
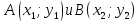 -
координаты точек
-
координаты точек

-
Параметрические уравнения прямой в пространстве
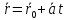
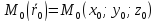 -фиксированная
точка лежащая на прямой;
-фиксированная
точка лежащая на прямой;
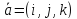 -направляющий
вектор.
-направляющий
вектор.
![]()
![]()
![]()
-
Угол между прямыми в пространстве
Угол между прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым
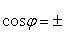

-
Условия параллельности и перпендикулярности двух прямых в пространстве
Условие параллельности двух прямых в пространстве:
![]()
![]()
![]()
Условие перпендикулярности двух прямых (6) имеет вид
mm1 + nn1 + pp1 = 0.
-
Угол между прямой и плоскостью
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
|
sin φ = |
| A · l + B · m + C · n | |
|
√A2 + B2 + C2 · √l2 + m2 + n2 |
-
Условия параллельности и перпендикулярности прямой и плоскости
-
В случае параллельности прямой
 и плоскости
и плоскости
 угол между ними равен 0, следовательно
угол между ними равен 0, следовательно
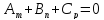
-
В случае перпендикулярности прямой и плоскости совпадает с условием параллельности этой прямой и перпендикуляра к плоскости

-
Как найти координаты точки пересечения прямой и плоскости
Возможны три варианта взаимного расположения прямой и плоскости в пространстве:
-
прямая лежит в плоскости;
-
прямая параллельна плоскости;
-
прямая пересекает плоскость.

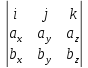 =i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
=i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =