Теоретическая часть

1. Аналитическое моделирование передачи данных

В настоящей лабораторной работе автоматизированное проектирование ведется с использованием среды моделирования MATLAB 7.0+Simulink и сводится к подбору параметров ГСК, обеспечивающих заданную вероятность передачи информации в каналах связи, описываемых различными аналитическими моделями.

1. Модели дксбп (двоичного симметричного канала без памяти)

В качестве аналитических моделей цифрового канала связи без памяти (двоичного симметричного канала с независимыми ошибками) используется биномиальное либо пуассоновское распределение ошибок. Каналы без памяти – радиоканалы, спутниковые – характеризуются независимыми ошибками.

Модель 1

(1)

Модель 2

(2)

где - вероятность i-кратной ошибки среди n передаваемых символов;

- вероятность ошибки при передаче элементарного сигнала (вероятность ошибки на символ);

- среднее число ошибок среди n передаваемых символов,

2. Модели дкссп (двоичного симметричного канала с памятью)

Каналы с памятью хорошо описывают коммутируемые каналы (т.к. раньше каналы были электромагнитными, переключения приводили к пакетирующимся ошибкам). Пакеты, всплески ошибок также могут возникать на территории или вблизи промышленных предприятий, силовых линий и т. д.

1. Модель Пуртова

В качестве аналитической модели цифрового канала с памятью (однородного двоичного канала с пакетированием или группирующимися ошибками) используется модель Пуртова:

(3)

Где - вероятность не менее i группирующихся ошибок среди n символов;

- коэффициент пакетирования ошибок (в данной лабораторной работе принято =0,3-0,7.

2. Модель Гильберта-Элиота

Это четырехпараметрическая модель ДСДКП с глубиной памяти l=1. В отличие от модели Гильберта, в данной модели допускается появление ошибок как в “хорошем” (G-good), так и в “плохом” (В-bad) состояниях канала соответственно с вероятностями p_g и p_b.

Граф марковской цепи показан на рис. 1.

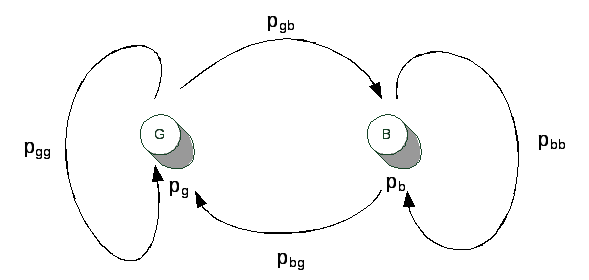
Рис. 1. Граф переходов модели Гильберта – Элиота

Модель Гильберта – Элиота полностью описывается четырьмя параметрами: p_g, p_b, p_bg, p_gb. Вероятности p(G) и p(B) определяются по (4) и (5).

p(G) =p(G)p_GG+p(B)p_BG=p(G)p_GG+ (1 -p(G))p_BG,

. (4)

p(B) = p(B) p_BB + p(G) p_GB = p(B) p_BB + (1 - p(B)) p_GB,

. (5)

Вероятность ошибки на символ:

(6)

Вероятность ошибки кратности i среди n символов, передаваемых по ДСДКП:

(7)

Вероятность искажения кодовой серии длины n:

(8)

3. Вероятностно-временные характеристики каналов

В каналах с независимыми ошибками (например, описываемых моделью 1), использующими для передачи групповые систематические коды, исправляющие s и менее ошибок, вероятностные показатели определяются следующим образом:

(9)

Здесь n – длина кода (n,m) с , определяемая из границы Хемминга.

Исходя из этого, безызбыточному коду (s=0) соответствуют формулы:

Для ГСК, исправляющего s и обнаруживающего (s+1) ошибку (с четным кодовым расстоянием ), рассматриваемого в данной лабораторной работе

(10)

,, - соответственно вероятности правильной передачи сообщения, стирания сообщения (обнаружения ошибки) и трансформации сообщения (необнаружения ошибки).

В каналах с группирующимися ошибками, описываемых моделью (3), в которых применяются (n,m,d) - коды, исправляющие s ошибок, вероятностные показатели равны:

(11)

Следует отметить, что ГСК являются оптимальными для каналов с независимыми ошибками и не обеспечивают наилучшие показатели вероятности правильной передачи в каналах с группирующимися ошибками. В то же время известны групповые (n,m)-коды (перемежающиеся коды и пр.), оптимальные в каналах с памятью и исправляющие пакеты ошибок длины b и меньше. Для этих кодов число избыточных символов k определяется из соотношения:

(12)

Скорость передачи данных с использованием ГСК-кода определяется по формуле:

(13)

Приведенные соотношения (1)-(13) положены в основу алгоритмов и программ автоматизированного проектирования цифровых каналов, использующих ГСК для обеспечения заданной верности передачи.