Кинематика вращательного движения
Лекция 1б
•Абсолютно твёрдое тело — модельное понятие классической механики, обозначающее совокупность материальных точек, расстояния между которыми сохраняются в процессе любых движений, совершаемых этим телом.
•Иначе говоря, абсолютно твердое тело не только не изменяет свою форму, но и сохраняет неизменным распределение массы внутри.
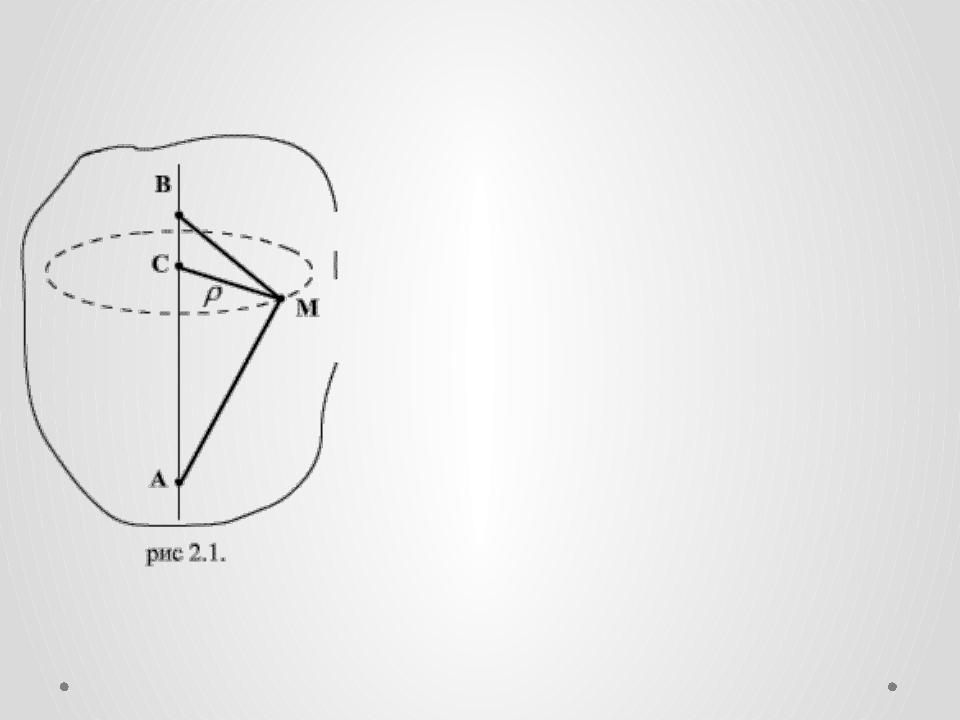
•Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной.
•В противном случае расстояния АС и ВС должны были бы
изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными,
называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.
•Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ.
•При вращении твердого тела расстояния М А и МВ и
расстояние ρ точки М до оси вращения должны оставаться неизменными.
•Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси.
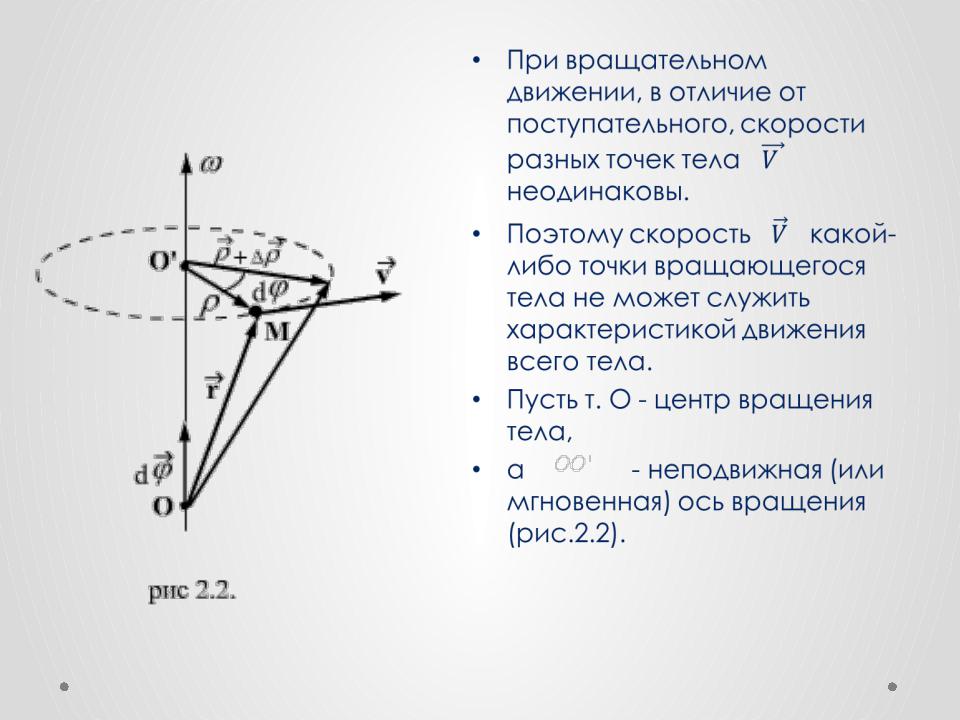
•При вращательном
движении, в отличие от
поступательного, скорости
разных точек тела неодинаковы.
• Поэтому скорость какой-
либо точки вращающегося тела не может служить
характеристикой движения
всего тела.
•Пусть т. О - центр вращения тела,
• а - неподвижная
(или мгновенная) ось вращения (рис.2.2).
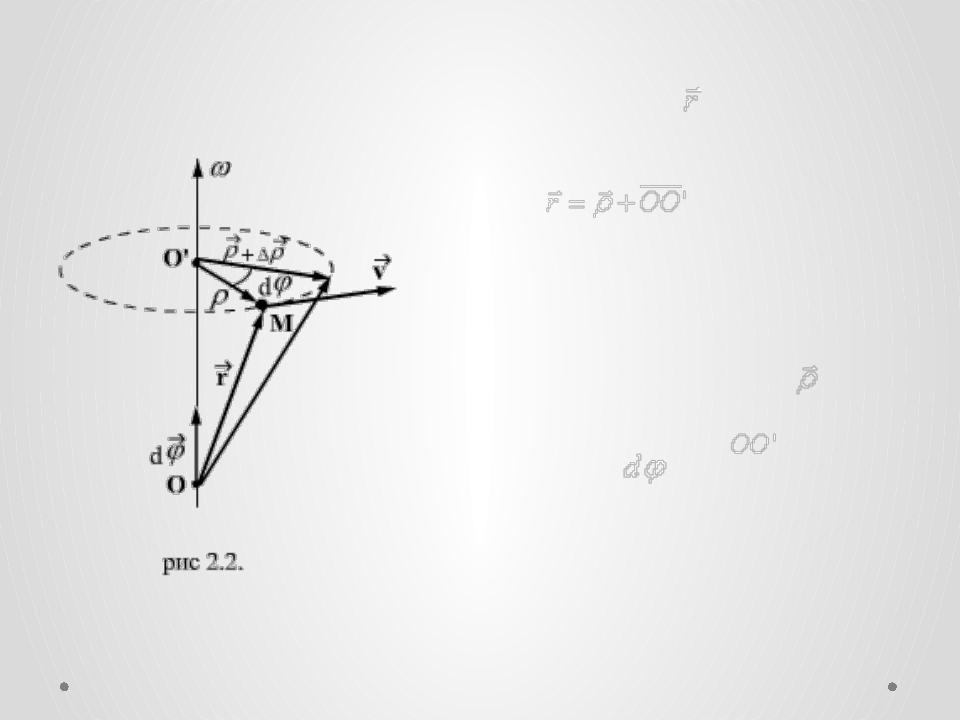
•Положение произвольной т. М тела будем задавать с помощью радиус-вектора , проведенного из центра О. Из рисунка видно, что:
•где - 
радиус-вектор, проведенный в точку дуги окружности, по которой движется т. М.
•За малое время вектор поворачивается в плоскости
перпендикулярной |
, на |
|
малый угол |
. |
|
•На такой же угол поворачивается
за время dt радиус-вектор любой другой точки тела, т.к. в противном случае расстояние
между этими точками должны были измениться.
•Таким образом, угол поворота
характеризует перемещение всего вращающегося тела за
малый промежуток времени.
•Удобно ввести вектор элементарного (малого) поворота
тела , численно равный
и направленный вдоль
мгновенной оси так, чтобы из его конца поворот тела был виден
происходящим против часовой
стрелки.
Угловая скорость
Векторная величина
• |
называется угловой скоростью тела. Вектор |
направлен |
|
вдоль оси вращения в сторону, определяемую правилом винта, |
|
|
т.е. также как вектор элементарного поворота |
. |
• |
Модуль вектора угловой скорости равен |
. |
• |
Вращение с постоянной угловой скоростью называется |
|
|
равномерным, при этом: |
|
• т.е. при равномерном вращении показывает, на какой угол поворачивается тело за единицу времени.
Период и частота обращения
• Время, за которое тело совершает один оборот, т.е.
поворачивается на угол , называется периодом обращения. Так как промежутку времени
соответствует угол поворота ∆ = 2 , то
откуда
• Число оборотов в единицу времени |
равно: |
•отсюда следует, что угловая скорость
• В случае неравномерного движения |
не остается |
постоянной. |
|
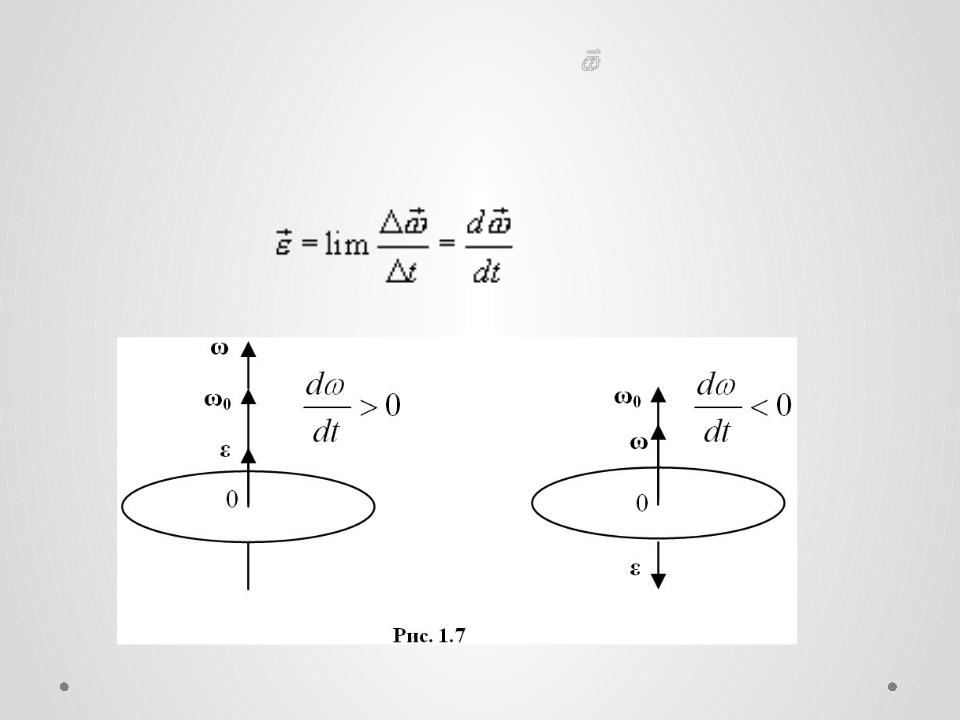
•Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:
• |
В случае вращения тела вокруг неподвижной оси |
|
||
|
изменение вектора |
обусловлено только |
|
|
|
изменением его численного значения. |
|
|
|
• |
При этом вектор углового ускорения |
направлен |
||
|
вдоль оси вращения в ту же сторону, что и |
при |
||
|
ускоренном вращении |
и при |
|
|
• замедленном в обратном направлении.