ответы_канева

1. Модель данных

Это набор данных, который представлен в виде таблицы данных.

Столбцы отвечают за факторы, которые действуют на процесс.

Значение переменной Y, для которой надо сделать прогноз, в общем случае зависят от времени t и m факторов.

Таким образом, переменная Y является функцией от времени t и факторов X.

2. Общая схема построения прогноза

Построение прогноза – это, прежде всего построение модели данных, где вычисление прогнозного значения является заключительным этапом построения модели.

Этап 1. Подготовка исходных данных.

Это, этап предварительного анализа имеющихся данных:

• Анализ резко выделяющихся наблюдений

• Восстановление пропущенных данных

• Сбор информации о факторах и исследование их влияния на прогнозируемую переменную

Этап 2. Построение моделей

На этом этапе строится несколько функций построения модели.

Известные методы прогнозирования:

1. Казуальные модели (регрессионный, множественный)

2. С помощью временных рядов (декомпозиция, скользящее среднее, экспоненциальное сглаживание, авторегрессионные модели, модель ARIMA, нейронные сети)

Этап 3. Анализ полученной модели

Анализ подразумевает проведения двух этапов исследования:

1. Исследование КАЧЕСТВА прогнозной модели, на основе остатков, использую MAD, MSE, R²

2. Исследование ТОЧНОСТИ прогнозной модели MAPE

Этап 4. Вычисление прогнозного значения

На основе отобранных функций прогнозирования вычисляются прогнозные значения. Прогноз бывает: точечным и интервальным.

Этап 5. Дополнительная корректировка прогноза

Если построена хорошая модель, то она используется не однократно, на протяжении некоторого периода времени. В этом случае модель продолжает совершенствоваться путем добавления в нее новых данных и пересчета, соответствующих ее параметров, при этом может потребоваться полное или частичное перестроение модели.

3. Виды связей в статистике

Происходящие явления и процессы органически связаны между собой, зависят друг от друга и обуславливают друг друга.

Существуют два вида связи: функциональная и корреляционная, которые обусловлены двумя типами закономерности: динамической и статистической.

При функциональной связи каждому значению одной величины соответствует одно или несколько вполне определенных значений другой величины. Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функций и между аргументом и функциями нельзя установить строгой зависимости, называется корреляционной. 

Классификация корреляционной связи: 1. по тесноте связи: отсутствует, слабая, умеренная, сильная. 2. По направлению: прямая и обратная.

4. Оценка параметров

Пусть θ – точное значение величины, вычисление которой является целью поставленной задачи (параметр);

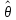– оценка искомой величины (найденное каким либо образом приближенное значение искомой величины, параметра). В статистике оценка рассчитывается по выборке. Когда оценка определяется одним числом, она называется точной оценкой. В статистике оценка рассчитывается по выборки. // приближенное значение // некоторая функция от выборки

Желательные требования к оценки:

1. Несмещенность, когда математическое ожидание совпадает с истинным значением параметра (отсутствие систематической ошибки);

2. Состоятельность (улучшение оценки увеличением объема выборки);

3. Эффективность (обладает минимальным рассеиванием относительно истинного значения параметра θ).

Рассчитанная по выборке точечная оценка 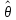параметра θ – является приближенным значением θ.

Мерой нашего доверия оценки будем считать вероятность γ того, что погрешность оценки не превысит заданной точности ε.

Интервал вида с заранее заданной вероятностью γ заранее накрывает истинное значение параметра θ.

При этом вероятность γ, называется доверительной вероятностью (надежностью), а сам интервал – доверительный интервал (доверительной оценкой) для параметра θ.

1. Задается γ;

2. Задается точность оценки ε и по выборки …

3. Высчитываются границы интервала .

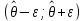Чем хуже доверительный интервал для оценки параметра, тем лучше.

На длину интервальной оценки влияет мощность выборки и доверительная вероятность.

5. Проверка статистических гипотез

Гипотеза в статистике – есть некое научное предложение, которое необходимо проверить и далее принять или опровергнуть.

Статистическая проверка гипотезы состоит в выяснение того, согласуются ли результаты наблюдений (выборочные данные) с нашим предположением.

Если нулевая гипотеза отвергается, в то время как в генеральной совокупности она справедлива, такая ошибка, называется ошибкой первого рода. А ее вероятность – уровнем значимости.

Если H₀ принимается, а в генеральной совокупности справедлива Н₁, такую ошибку, называют ошибкой второго рода. А ее вероятность – β (1- β, называется мощностью критерия).

Алгоритм проверки гипотез

1. Формируется основная и альтернативная гипотезы

2. Задается уровень значимости α € [0.001; 0.1]

3. Выбирается статистический критерий k

4. По таблицам распределения k найти границу критической области k_кр, вид критической области определить по виду альтернативной гипотезы H_1

5. По выборочным данным вычислить наблюдаемое значение критерия k_набл

6. Принять статистическое решение

6. Корреляционный анализ

Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами.

Положительная корреляция
Отрицательная корреляция
Отсутствие корреляции

Коэффициент корреляции, есть среднее значение для каждого параметра выборки.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:

1. Коэффициент корреляции значимо отличается от нуля (т.е. есть взаимосвязь между величинами)

2. Отличие между двумя коэффициентами корреляции значимо

7. Восстановление пропущенных данных

Считается, что чем больше имеется исходных данных, тем точнее можно рассчитать параметры функции прогнозирования и соответственно прогноз. Но с другой стороны методы восстановления данных не гарантируют, что на основе данных, в составе которых присутствуют восстановленные значения, можно получить более точные значения параметров, чем при basic прогнозировании.

Если в наличии имеется достаточно большое количество точек данных, то можно удалить те точки данных, где отсутствуют значения факторов, при условии, что количество удаляемых точек не велико.

Один из способов восстановления данных:

1. Строится функция регрессии фактора

2. Вычисляется функция регрессии;

Вычисляется функция регрессии, где пропущены исходные данные, вычисленные значения принимаются за искомые значения фактора.

Факторы по которым строится регрессии, называется инструментальными переменными (инструментами).

Требование:

1. Они должны коррелировать с фактором, для которого строится функция регрессии. (должна быть зависимость)

2. Значения инструментов должны быть, по возможности, детерминировать (не зависеть от случайных значений).