UP_Nelineynye_sistemy_upravlenia

туды и частоты), а затем – анализ его устойчивости. Итак, предполагаем существование колебательного периодического решения x t x t T . Тогда и

выходная величина нелинейного элемента будет периодической: y t y t T .

Записывая передаточную функцию линейной части системы в форме дробно-рациональной функции W p R p Q p , уравнение (2.63) можно переписать как

Частоту и амплитуду автоколебаний можно определить, если подобрать такой коэффициент с, что корни характеристического уравнения будут чисто мнимыми.

Далее, предполагая, что гипотеза фильтра выполнена, заметим, что можно пренебречь составляющими процесса на выходе линейной части с высшими частотами 2 , 3 … (ввиду малости для них коэффициента передачи) и считать, что на выходе линейной части системы имеется гармонический сигнал с частотой . На выходе нелинейной части системы, конечно, появятся составляющие с высшими частотами.

Однако, поскольку эти высшие гармоники не вызывают существенной реакции на выходе линейной части системы, можно не учитывать их влияние на динамику замкнутой системы. Следовательно, при исследовании замкнутой системы можно приближенно считать, что как вход, так и выход нелинейного элемента являются гармоническими колебаниями (в общем случае эти колебания могут быть несимметричными и содержать постоянную составляющую), благодаря чему и выполняется гармоническая линеаризация нелинейности.

Согласно высказанным гипотезам будем искать колебательное решение

и попытаемся подобрать величины a (амплитуда) и (частота) так, чтобы уравнения (2.63) и (2.64) удовлетворялись тождественно. Тогда выходной процесс будет также периодическим, его разложение в ряд Фурье будет иметь вид:

41

y t x t a sin t a0 ak sin k t bk cos k t .

k 1

Согласно принятой гипотезе можно ограничиться только слагаемыми с частотой не выше частоты основной гармоники, т. е. принять

y t a0 a1 sin t b1 cos t ,

где коэффициенты разложения Фурье определяются по следующим выражениям

где t . Здесь стоит отметить, что коэффициенты a0 , a1 и b1 зависят только от вида нелинейной функции и амплитуды.

Исследование выражений (2.68)–(2.70) показывает, что для однозначных симметричных нелинейных характеристик (т. е. в случае, когда выходной процесс заданного звена тоже есть гармоника частоты , совпадающая по фазе с входным процессом, но имеющая амплитуду a1 ) справедливо следующее:

sin t x t a . Подставляя это выражение в (2.71), получим

y t a1sin t aa1 x t q a x t ,

где q a a1a – коэффициент гармонической линеаризации. Таким образом,

при сделанных предположениях рассматриваемое звено ведет себя как линейное безынерционное звено y t q a x t с коэффициентом передачи

Тогда в установившемся колебательном режиме можно перейти от нелинейной системы к линейной.

Для неоднозначных симметричных нелинейных характеристик (в этом случае происходит фазовый сдвиг)

42

Таким образом, для нахождения частоты и амплитуды колебаний необходимо построить характеристику, обратную амплитудно-фазовой характеристике линейной части системы, взятой с обратным знаком. Далее на той же комплексной плоскости построить для рассматриваемого случая характеристику коэффициента гармонической линеаризации (в общем случае ампли- тудно-фазовую характеристику звена, определяемого передаточными функциями вида (2.72) и (2.74)). Найти точки пересечения, которые и дадут значения искомых величин частоты и амплитуды автоколебаний. Дополнительно необходимо провести анализ устойчивости найденных параметров автоколебаний.

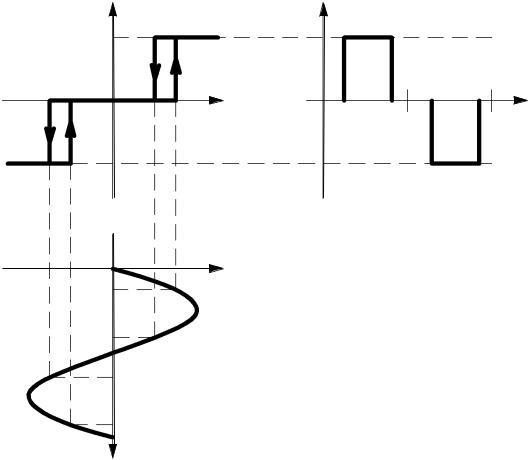
Приведем пример вычисления коэффициента гармонической линеаризации для нелинейного звена с петлевой характеристикой релейного типа с гистерезисом при условии, что амплитуда гармонических колебаний больше r. График, отражающий прохождение гармонического сигнала через звено с насыщением, приведен на рис. 2.19.

x1

u1

u2

x1 = asin(u)

u3

u4

u = ωt

Рис. 2.19. Построение функции на выходе релейного звена с гистерезисом

44

Вычислим коэффициент гармонической линеаризации q a согласно выражению (2.75). Следует отметить, что выходную функцию можно рассматривать только на интервале u t 0; . При этом необходимо удвоить значение подынтегрального выражения. Кроме того, сама выходная функция на этом отрезке может быть описана следующим выражением:

где абсциссы u1 и u2 вычисляются из решения следующих уравнений:

a sin u1 r , a sin u2 mr .

Таким образом,

u1 arcsin ar ,

Тогда коэффициент гармонической линеаризации можно вычислить так:

(2.79)

Аналогичным образом найдем коэффициент гармонической линеаризации b a согласно выражению (2.76):

45

т. е. выполняется баланс фаз и амплитуд входного и выходного сигналов. Тогда с учетом равенства (2.77) получим

Равенства (2.86) и (2.87) используются для графоаналитического решения задачи. Вариант такого решения при использовании (2.87) приведен на рис. 2.21.

jIm

Re

1

1 W ( j)

2

q( A) + jb(A)

Рис. 2.21. Определение параметров автоколебаний

Для нахождения графоаналитического решения на комплексной плоскости строится величина, обратная амплитудно-фазовой характеристике линейной части, взятая с противоположным знаком, и кривая гармонического коэффициента передачи. На первой точками отмечают ряд значений частот 1 ,2 , …, на второй – значения амплитуд A1, A2 , …. В точках пересечения кривых с помощью интерполяции между соседними с ними значениями i ,

47

i1 и A j , Aj 1 находят значения частоты 0 и амплитуды A0 автоколе-

баний.

В приведенном примере (рис. 2.21) две точки пересечения, а значит, и два набора параметров автоколебаний. Дополнительно решается вопрос устойчивости автоколебаний. Если при увеличении амплитуды точка выходит из области, охватываемой амплитудно-фазовой характеристикой системы, то колебания будут устойчивыми.

3. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ

3.1. Постановка задачи устойчивости нелинейных систем по А. М. Ляпунову

Характерной особенностью линейных систем является возможность представления движения системы суммой свободной и вынужденной составляющих. Показателем устойчивости является стремление к нулю свободной составляющей при t . Для нелинейных систем в связи с неприменимостью принципа суперпозиции невозможно разделить процесс на свободную и вынужденную составляющие, поэтому процесс в нелинейных системах необходимо рассматривать как единое целое, что значительно усложняет исследование устойчивости.

Для нелинейных систем существует несколько понятий устойчивости в зависимости от областей возможных отклонений от состояния равновесия и наличия внешних возмущений.

В зависимости от наличия внешних воздействий все системы могут быть разделены на автономные и неавтономные системы. В автономных системах возможно два вида движений – равновесные состояния и автоколебательные режимы, устойчивость которых необходимо исследовать. Для неавтономных систем необходимо также исследовать устойчивость вынужденных режимов.

Естественным стремлением при исследовании устойчивости систем было стремление к применению единых методов, аналогичных исследованию устойчивости линейных систем. Это стремление привело к постановке А. М. Ляпуновым задачи исследования устойчивости. Основополагающим моментом в теории устойчивости по Ляпунову было понятие возмущенных и невозмущенных движений. Под невозмущенным движением понимается любое движение xн t , устойчивость которого исследуется. Это может быть со-

48

стояние равновесия, автоколебательный режим или вынужденное движение. Это движение можно получить при фиксированных начальных условиях, параметрах системы или внешних возмущениях.

Всякое другое движение считается возмущенным. Можно, в частности, считать, что любое возмущенное движение получается при подаче в момент времени t 0 импульсного внешнего возмущения. Состояние равновесия или автоколебательного режима можно считать невозмущенным движением.

Для пояснения приведенного определения приведем пример. Пусть есть система с передаточной функцией

Если же рассматривать возмущенное движение при x 0 , то получим, что c1 k . Таким образом, уравнение возмущенного движения:

Можно сделать вывод, что решение (3.1) асимптотически устойчиво, так как согласно (3.4) при t xв t xн t 0. Однако не всякое асимптотически устойчивое решение устойчиво по Ляпунову.

Рассмотрим еще один пример. Пусть есть линейная система второго по-

Как и ранее, запишем невозмущенное и возмущенное решения уравнения (3.5) в виде xн x0 cos 0t , xв x0 cos 0t .

Модуль разности невозмущенного и возмущенного движения определя-

При t разность невозмущенного и возмущенного движения (3.6) не устанавливается и не стремится к нулю, поэтому нельзя говорить об асимптотической устойчивости.

Если условие xв t xн t 0 при t выполняется в малой области , то говорят об асимптотической устойчивости в малом; если область– ограниченная, то в большом; если , то об устойчивости в целом.

Если область – отрезок на оси, то говорят об устойчивости, но не асимптотической.

Все приведенные определения устойчивости могут быть отнесены к устойчивости состояния равновесия, автоколебательных и вынужденных режимов. Для суждения об устойчивости автоколебаний вводится понятие орбитальной устойчивости.

Периодическое движение (автоколебание) в фазовом пространстве изображается некоторой замкнутой кривой G G x1, ..., xn . Представляя любую

фазовую траекторию геометрическим местом точек конца вектора , мож- x t

но для любого момента времени определить кратчайшее расстояние от конца

50