
UP_Nelineynye_sistemy_upravlenia
.pdf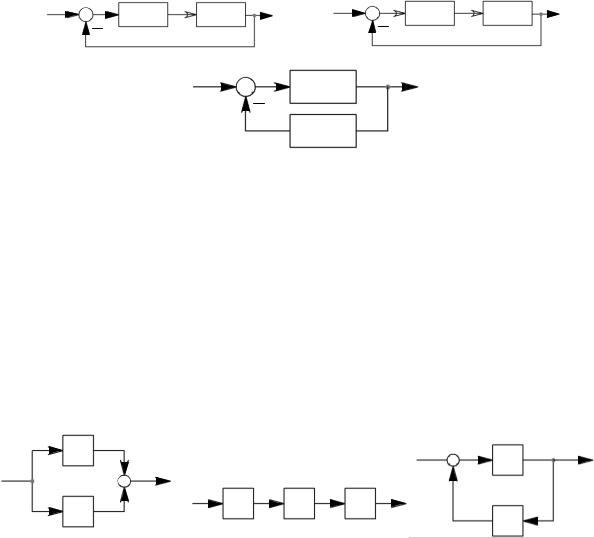
В курсе рассмотрены некоторые методы, пригодные для анализа нелинейных систем с определенной структурой и с некоторым типом нелинейностй. Эти методы пригодны для нелинейных систем, содержащих линейную часть и один статический нелинейный элемент. Возможные структурные схемы изучаемых далее нелинейных систем приведены на рис. 1.9.
φ WЛ(p)
WЛ(p)
а
 WЛ(p)
WЛ(p)  φ
φ
б
WЛ(p)
φ
в
Рис. 1.9. Система с нелинейностью:
а – во входной цепи; б – в выходной цепи; в – в цепи обратной связи
Из рассмотренных структурных схем следует, что нелинейные системы состоят из линейной динамической части и одного статического нелинейного звена. Если система содержит несколько нелинейных элементов, то ее в некоторых случаях можно свести к системе с одной нелинейностью, заменив нелинейные элементы одним элементом с результирующей статической характеристикой. Рассмотрим метод графического определения такой результирующей статической характеристики для трех различных соединений нелинейных звеньев, приведенных на рис. 1.10.
φ1 |
z1 |
|
|
|
xвх |
xвых |
x |
z |
|
|
|
± |
φ1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
z1 |
z2 |
|
z3 |
|
|
φ1 |
|
φ2 |
φ3 |
|
|
φ2 |
z2 |
|
|
|
z |
φ2 |
а |
|
|
б |
|
|
в |
Рис. 1.10. Типовые соединения нелинейных элементов:
а – параллельное; б – последовательное; в – встречно-параллельное
Параллельное соединение нелинейных звеньев приведено на рис. 1.10, а. Для нахождения результирующей характеристики эквивалентного нелинейного элемента необходимо построить зависимости z1 1 x и z2 2 x , после чего просуммировать их ординаты, как это показано на рис. 1.11.
11

|
z |
Последовательное |
соединение |
нелиней- |
|
|
|
|
|
||
|
|
|
ных звеньев приведено на рис. 1.10, б. Процесс |
||
|
z |
нахождения результирующей характеристики |
|||
|
|
|
|||
|
z1 |
приведен на рис. 1.12. В первом квадранте по- |
|||
|
z2 |
строена статическая характеристика |
первого |
||
|
|
x |
входного звена цепочки 1 x , во втором |
||
|
|
||||
|
Рис. 1.11. Построение |
квадранте – характеристика следующего звена |
|||
|
характеристики параллельного |
2 z1 , но так, что ее оси повернуты на 2 |
|||
|
соединения |
||||
нат характеристики 1 x , |
радиан: ось абсцисс z1 |
совпадает с осью орди- |
|||
а ось ординат z2 направлена по отрицательной |
|||||
полуоси абсцисс.
Для построения результирующей характеристики задаемся некоторым значением x t (например, точка 1). Затем из выбранной точки 1 восстанавливаем перпендикуляр до пересечения с характеристикой z1 1 x (точка 2). Далее из точки 2 проводим отрезок, параллельный горизонтальной оси, до пересечения с характеристикой z2 2 x (точка 3).
Длина отрезка 0а от начала координат до основания перпендикуляра, опущенного из точки 3 на ось абсцисс, равна искомому значению z2 , соответствующему входному значению x t .
2 |
z1 |
|
1 |
|
|
|
|
3 |
|
2 |
|
z2 |
0 |
1 |
x |
a |
|
|
|
4 |
5 |
A |
z2 |
 z2
z2
Рис. 1.12. Построение результирующей характеристики последовательного соединения
Однако удобнее построить характеристику z2 x в четвертом квадранте, поэтому перенесем точку 3 с помощью биссектрисы квадрантного угла 0А.
12

Для этого из точки 3 проведем вертикальный отрезок 3-4 до пересечения с 0А (точка 4) и дальше из точки 4 – горизонтальную линию 4-5 до встречи с продолжением перпендикуляра 1-2 (точка 5). Точка 5 принадлежит статической характеристике z2 x нелинейного звена, эквивалентного соединению двух нелинейных элементов. Остальные точки результирующей характеристики получаются аналогичным образом.
Встречно-параллельное соединение нелинейных звеньев приведено на рис. 1.10, в. Процесс построения результирующей характеристики данного соединения приведен на рис. 1.13.
|
|
|
xвых |
|
|
|
φ2 |
xвых |
|
xвых |
|
φ2 |
|
|
φ1 |
xвых |
|
|||
|
|
|
||||
2 |
1 |
3 |
|
|
φ1 |
|
2 |
3 |
1 |
||||
|
|
|
z |
|
|
|
xвх |
xвх |
б |
0 |
а |
в |
0 б в |
а |
|
а |
|
|
б |
|
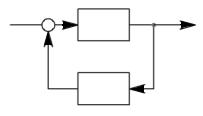
Рис. 1.13. Построение характеристики встречно-параллельного соединения: а – отрицательная обратная связь; б – положительная обратная связь
Сначала рассмотрим случай отрицательной обратной связи. В первом квадранте на рис. 1.13, а построена характеристика нелинейного звена φ1, находящегося в канале прямой связи. Зададимся некоторым значением xвых. Теперь необходимо найти значение xвх , которое будет соответствовать выбранному значению выхода. Если бы значение обратной связи было равно нулю, то значение xвх можно было бы найти непосредственно из характери-
стики φ1: xвх 0а .
При наличии отрицательной обратной связи отрезок 0а будет равен результирующему входному воздействию: 0а xвх 2 xвых . Поэтому для определения xвх к величине 0а необходимо прибавить 2 xвых 0б . Если во втором квадранте построить характеристику z 2 xвых обратной связи, направив ось z влево, то величина xвх будет равна сумме отрезков 0а и 0б , т. е. расстоянию от точки 2 до точки 1. Перенеся этот отрезок измерителем по горизонтали вправо до совмещения его левого конца с осью ординат, полу-
13
чим точку 3 результирующей статической характеристики. Аналогично найдем и остальные точки.
В случае положительной обратной связи (рис. 1.13, б) характеристику z 2 xвых удобнее строить в первом квадранте, совместив ось xвх и ось z . Однако в этом случае искомая абсцисса точки результирующей статической характеристики равна разности 0в 0а 0б , т. е. расстоянию между кривыми
1 xвх z и 2 xвых .
Приведенные преобразования возможны, если между нелинейными элементами нет динамических звеньев. В противном случае такие преобразования невозможны. Это объясняется тем, что для нелинейных систем не выполняется свойство коммутативности.
2. ИССЛЕДОВАНИЕ ДИНАМИКИ НЕЛИНЕЙНЫХ СИСТЕМ НА ФАЗОВОЙ ПЛОСКОСТИ
2.1. Обобщенная математическая модель нелинейных систем
Проектирование нелинейных систем на этапе теоретических исследований и разработок, так же как и проектирование линейных систем, осуществляется либо методами анализа, либо методами синтеза. Дополнительно для нелинейных систем необходимо решать задачу устранения влияния непреднамеренных нелинейностей или задачу коррекции системы нелинейными устройствами для придания ей особых свойств, которые невозможно получить в линейном варианте. Методика проектирования нелинейных систем на этапе теоретических разработок ничем не отличается по постановке от аналогичной задачи для систем линейных.
Для анализа процессов необходимо сначала составить (разработать) математическую модель (систему дифференциальных уравнений, структурную схему и т. д.), а затем, используя методы решения дифференциальных уравнений, выполнить анализ по полученным решениям. При всем разнообразии методов решения дифференциальных уравнений их можно разделить на не-
xвх |
y |
x |
сколько групп: аналитическое решение; |
числен- |
z |
± |
WЛ(p) |
ное моделирование с использованием ЭВМ. |
|
|
||||
|
|
|
||
|
|
|
Представление о математической |
модели |
нелинейной системы можно получить по структурной схеме нелинейной системы, приведенной на рис. 2.1.
14
Пусть передаточная функция линейной части системы записана в виде дробно-рациональной функции
W p |
R p |
|
, |
|
|
Q p |
|
||||
|
|
|
|
||
где Q p и R p – операторы следующего вида: |
|
||||
Q p a |
pn a pn1 |
a , |
(2.1) |
||
0 |
1 |
|
n |
|
|
R p b pm b pm1 |
b . |
|
|||
0 |
1 |
|
|
m |
|
Тогда дифференциальное уравнение линейной части системы можно за- |
|||||
писать в операторной форме как |
|
|
|
|
|
xQ p R p y , |
(2.2) |
||||
где y – рассогласование, определяемое выражением |
|
||||
y xвх z xвх x . |
(2.3) |
||||
Выражение (2.2) можно переписать с учетом (2.3): |
|
||||
xQ p x R p xвхR p . |
(2.4) |
||||
Если положить оператор R p 1, то (2.4) преобразуется к виду |
|
||||
xQ p x xвх . |
(2.5) |
||||
Окончательно можно перейти от записи (2.5) в операторной форме к записи дифференциального уравнения во временной области с учетом (2.1):
a |
d n x |
a |
d n1x |
a |
|
x x x . |
(2.6) |
|
|
|
|||||
0 dt n |
1 dt n1 |
|
n |
вх |
|
||
Другой формой записи дифференциального уравнения (2.6) является запись в форме Коши в виде системы n нелинейных дифференциальных уравнений. Эта форма представления получила название модели в переменных состояния. Переход от (2.6) к модели в переменных состояния осуществляется следующим образом. Выходная переменная переобозначается как x t x1 t .
Далее вводится ряд переменных состояния, которые имеют смысл производной от предшествующей переменной:
dx1 t |
x2 |
t , |
||||||
|
dt |
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(2.7) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
dx |
|
t |
xn t . |
|||||
|
n-1 |
|
|
|
|
|||
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
||

Таким образом, получаем систему (2.7), содержащую n 1 уравнение. Последнее уравнение системы получается из уравнения (2.6):
dxn |
|
a1 |
x |
|
an1 |
x |
|
an x1 x1 |
|
xвх |
. |
(2.8) |
|
|
|
|
|
||||||||
|
|
|
n |
2 |
|
a0 |
|
a0 |
|
|||
dt |
|
a0 |
|
a0 |
|
|
|
|||||
В общем случае для i-го уравнения системы (2.7), (2.8) можно записать уравнение dxi  dt fi x1, x2 , , xn , xвх , где i 1, 2, , n .
dt fi x1, x2 , , xn , xвх , где i 1, 2, , n .
Как известно, общих методов решения нелинейных дифференциальных уравнений нет. Поэтому получение решений xi xi t затруднительно.
Для анализа простейших нелинейных систем второго и третьего порядков были разработаны различные простые графоаналитические методы анализа. Одним из таких методов является метод фазового пространства, в частном случае – метод фазовой плоскости.
2.2. Метод фазового пространства
Состояние системы определяется физическими величинами – переменными состояния xi , i 1, 2, , n , в каждый момент времени. При обычном
x |
|
подходе анализ динамики системы заключает- |
|
|
ся в исследовании поведения xi xi t как не- |
|
|
которой функции времени, что показано на |
|
|
рис. 2.2. |
|
|
При исследовании динамики систем в фа- |
|
t |
зовом пространстве в качестве координатных |
|
осей используются переменные состояния xi , |
|
Рис. 2.2. Анализ решения |
|
|
во временной области |
|
i 1, 2, , n . Например, для системы второго |
|
|
порядка переменных состояния будет две ( x1 и x2 ), и динамику системы можно исследовать на фазовой плоскости. При-
|
x2 |
|
мер фазовой траектории для системы второго |
|
x20 |
t = 0 |
|
порядка приведен на рис. 2.3. |
|
|
x10 |
x1 |
Каждому моменту времени t соответствует |
|
|
определенное состояние (фаза) системы, опреде- |
|||
|
|
|
||
|
|
|
ляемое значениями x1 t и x2 t . Так, например, |
|
|
|
|
для момента времени t t0 |
переменные состоя- |
Рис. 2.3. Фазовая траектория |
ния принимают значения |
x1 x10 , а x2 x20 . |
||
системы второго порядка |
Точка, соответствующая этим значениям, назы- |
|
|
|
16 |

вается изображающей точкой. С течением времени состояние системы изменяется, и точка перемещается в фазовом пространстве, так как переменные по координатным осям, определяющие фазу системы, изменяются. Перемещение точки будет происходить по линии, которая называется фазовой траекторией. Для фиксированных моментов времени положение изображающей точки показано на рисунке. Свойства системы полностью определяются поведением фазовой траектории в фазовом пространстве.
2.2.1. Методы построения фазовых траекторий
По существу, метод фазового пространства применим для систем не выше третьего порядка, поэтому чаще всего исследования проводят на фазовой плоскости для систем второго порядка. Математическая модель системы
второго порядка в общем случае имеет вид: |
|
|||||||
dx1 t |
f1 x1, x2 |
, |
||||||
|
dt |
|
|
|
||||
|
|
|
|
|
|
|||
dx |
2 |
t |
|
x1, x2 , |
||||
|
|
|
|
|
f2 |
|||
|
dt |
|||||||
|
|
|
|
|||||
где x1 t и x2 t – фазовые координаты.
Во многих же случаях модель системы проще, а именно:
dx y,dt
(2.9)
dy f x, y .
dt
Фазовыми координатами являются x – выходная величина и y – ее производная.
Первый метод построения фазовых траекторий заключается в нахождении решения системы дифференциальных уравнений (2.9) одним из известных способов. В результате получаем систему решений
x x t , |
(2.10) |
|
|
y y t . |
|
Исключим из этих решений время. Для этого выразим его, например, из второго решения (2.10):
t y . |
(2.11) |
17

После этого подставим полученное равенство (2.11) в первое уравнение
системы решений (2.10), получим уравнение фазовой траектории вида
x x y y .
Второй метод основан на решении дифференциального уравнения с разделяющимися переменными. Для составления этого уравнения необходимо разделить первое уравнение системы (2.9) на второе. В результате получим
dy |
|
f x, y |
. |
(2.12) |
|
|
|||
dx |
|
y |
|
|
Если (2.12) умножить на произведение знаменателей дробей, стоящих в левой и правой частях, получим
(2.13)
Часто бывает так, что нелинейность f x, y имеет вид f x . Тогда (2.13) можно преобразовать к виду ydy f x dx , т. е. к дифференциальному уравнению с разделяющимися переменными. Для решения такого уравнения необходимо выполнить интегрирование обеих частей:
y2 f x dx C ,
2
где C – постоянная интегрирования, определяемая из начальных условий.
2.2.2. Общие свойства фазовых траекторий
Из системы (2.9) следует ряд важных свойств фазовых траекторий.
1. Уравнение фазовой траектории определяется дифференциальным уравнением вида (2.12) за исключением точек, где y 0 и f x, y 0 одновременно, через любую точку фазовой плоскости проходит однаединственная кривая, поэтому фазовые траектории нигде не пересекаются.
2. Так как при y dx dt 0 величина x только возрастает, то в верхней полуплоскости с увеличением времени изображающая точка движется по фазовой траектории слева направо. Соответственно в нижней полуплоскости движение происходит справа налево.
dt 0 величина x только возрастает, то в верхней полуплоскости с увеличением времени изображающая точка движется по фазовой траектории слева направо. Соответственно в нижней полуплоскости движение происходит справа налево.
3. В точках y 0, f x, y 0 , т. е. в неособых точках оси абсцисс, фазовые траектории пересекают ось абсцисс под прямым углом сверху вниз в правой и снизу вверх в левой полуплоскостях.
18
4. Точки фазовой плоскости, где f x, y 0 и y 0 , соответствуют остановке движения. Решение этой системы дает точки равновесия системы. Точка y 0 , x 0 также является точкой равновесия системы в начале координат.
5. В зависимости от вида функции f x, y существует одно решение или их множество, часть из них могут быть устойчивыми, а часть – неустойчивыми. Поэтому нельзя говорить об устойчивости нелинейной системы в целом, можно говорить об устойчивости некоторых ее равновесных состояний, или об устойчивости ее отдельных движений.
2.2.3. Фазовые траектории линейных систем
Рассмотрим фазовую траекторию линейной системы второго порядка
x 2hx 02 x 0 . (2.14) 1. Сначала рассмотрим методы построения фазовых траекторий на при-
мере линейной консервативной системы без вязкого трения, что соответ-
ствует случаю h 0 . Уравнение свободных колебаний линейной системы, в которой нет сил сопротивления движению, приводящих к рассеянию энергии, можно привести к виду
x 2 x 0. |
(2.15) |
0 |
|
В механической системе наличие члена |
x , выражающего ускорение, |
обусловлено массой движущегося тела. Член |
2 x выражает позиционную |
|
0 |
силу, пропорциональную перемещению. Она может быть обусловлена наличием пружины.
Проведем процедуру нахождения фазовой траектории обоими описанными методами.
А. Найдем уравнение фазовой траектории, составив дифференциальное уравнение с разделяющимися переменными. Для этого введем следующую систему переменных:
dx |
|
y, |
||
|
|
|||
(2.16) |
||||
dt |
||||
dy |
2 |
|||
|
|
|
0 x. |
|
|
|
|||
dt |
|
|
||
Уравнение фазовой траектории можно получить, разделив второе уравнение системы (2.16) на первое:
19

|
dy |
|
2 x |
|
|
|
|
|
0 |
. |
|
|
|
|
|||
|
dx |
|
y |
|
|
Далее оно приводится к дифференциальному уравнению с разделяющи- |
|||||
мися переменными: |
|
|
|
|
|
ydy 2 xdx 0 . |
(2.17) |
||||
|
|
0 |
|
|
|
Интегрирование (2.17) приводит к следующему виду записи фазовой |
|||||
траектории: |
|
|
|
|
|
|
y2 |
2 x2 |
|
c2 |
|
|
|
|||
|
|
|
0 |
|
|
, |
|
(2.18) |
|
|
|
2 |
2 |
2 |
|
|
|||||
|
|
|
|
|||||||
произвольная постоянная с зависит от начальных условий: c y2 |
2x2 |
, |
||||||||
|
|
|
|
0 |
0 |
0 |
|
|||
где y0 y 0 , а x0 x 0 . Кроме того, (2.18) может быть преобразовано к каноническому уравнению эллипса
|
|
x2 |
|
y2 |
1, |
(2.19) |
|
|
a2 |
b2 |
|||
|
|
|
|
|
||
полуоси которого a c 0 |
и b c . |
Таким образом, |
фазовые траектории |
|||
представляют собой семейство вложенных друг в друга эллипсов с центром в начале координат. Начало координат в данном случае – это особая точка, не принадлежащая ни одной из траекторий, так называемая точка типа «центр».
Выражение (2.19) можно упростить, если рассматривать движение не из произвольной точки, а из точки, лежащей на оси абсцисс. Тогда y0 0 , а выражение преобразуется к виду
|
x2 |
|
y2 |
1. |
(2.20) |
|
|
x2 |
x 2 |
||||
0 |
|
0 |
0 |
|
|
|
Б. Найдем уравнение фазовой траектории путем исключения из (2.15) |
||||||
времени. Уравнению (2.15) соответствует незатухающее движение с угловой частотой 0 . Зададимся таким набором начальных значений, что y0 0 , а x0 x 0 , т. е. будем рассматривать начало движения от одной из осей.
Характеристическое уравнение p2 02 0 для дифференциального уравнения (2.15) будет иметь два комплексно-сопряженных корня с вещественной частью, равной нулю:
p1,2 j 0 . |
(2.21) |
20 |
|
