Решение

1. Затраты на рекламу являются признак-фактором, а прибыль – признак-результатом.

2. Сведем расчеты в таблицу:

	x	y		x2	y2	xy
	15	29		225	841	435
	17	38		289	1444	646
	25	46		625	2116	1150
	40	64		1600	4096	2560
	32	62		1024	3844	1984
	34	70		1156	4900	2380
	28	60		784	3600	1680
	18	42		324	1764	756
	26	52		676	2704	1352
	20	40		400	1600	800
	19	44		361	1936	836
	16	32		256	1024	512
	36	68		1296	4624	2448
	42	65		1764	4225	2730
	24	54		576	2916	1296
	30	58		900	3364	1740
	38	79		1444	6241	3002
	44	85		1936	7225	3740
	22	34		484	1156	748
	42	97		1764	9409	4074
Сумма	568	1119		17884	69029	34869

1. Выборочные средние:

2. Выборочные дисперсии:

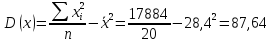
3. Среднеквадратическое отклонение:

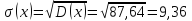
4. Поле корреляции:

5. Ширина интервала:

6. Аналитическая группировка:

   Группы	Количество,
   15 - 22.25	7	127	18.14	259	37
   22.25 - 29.5	4	103	25.75	212	53
   29.5 - 36.75	4	132	33	258	64.5
   36.75 - 44	5	206	41.2	390	78
   Итого	20	568		1119

7. Эмпирическая линия регрессии:

8. Можно сформулировать гипотезу о прямой связи между затратами на рекламу и прибылью.

9. На основе аналитической группировки можно сделать вывод о том, что при увеличении признак-фактора происходит в среднем увеличение признак-результата.

10. Внутригрупповая дисперсия:

		Результат
29	(29 – 37)2	64
32	(32 – 37)2	25
38	(38 – 37)2	1
42	(42 – 37)2	25
44	(44 – 37)2	49
40	(40 – 37)2	9
34	(34 – 37)2	9
Итого		182

Определим групповую (частную) дисперсию для 1–ой группы:

		Результат
54	(54 – 53)2	1
46	(46 – 53)2	49
52	(52 – 53)2	1
60	(60 – 53)2	49
Итого		100

Определим групповую (частную) дисперсию для 2–ой группы:

		Результат
58	(58 – 64.5)2	42.25
62	(62 – 64.5)2	6.25
70	(70 – 64.5)2	30.25
68	(68 – 64.5)2	12.25
Итого		91

Определим групповую (частную) дисперсию для 3–ой группы:

		Результат
79	(79 – 78)2	1
64	(64 – 78)2	196
65	(65 – 78)2	169
97	(97 – 78)2	361
85	(85 – 78)2	49
Итого		776

Определим групповую (частную) дисперсию для 4–ой группы:

Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:

Межгрупповая дисперсия относится на счет изучаемого фактора и называется факторной:

Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий:

, что совпадает с расчетами приведенными выше.

11. Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:

Связь между признаком Y фактором X весьма высокая

Коэффициент детерминации:

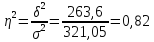
12. Корреляция:

Уравнение регрессии:

Линейное уравнение регрессии имеет вид:

13. Связь между признаком Y фактором X весьма высокая и прямая.

Коэффициент детерминации:

R²=0,92²=0,848

Т. е. В 84,8% случаев изменения x приводят к изменению y. Другими словами – точность подбора уравнения регрессии – высокая. Остальные 15,2 % изменения y объясняются факторами, не учтенными в модели.

14. Критерий Фишера:

Табличное значение критерия со степенями свободы – k₁ =1 и k₂=18, F_табл. = 4,41. Поскольку фактическое значение F > F_табл. , то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).